Содержание
- 2. Цель работы: Расширить область математических знаний. Развивать логическое мышление. Вывести общие формулы, позволяющие решать задачи интегрирования.
- 3. Задачи исследования: - собрать, изучить и систематизировать материал об интеграле; - рассмотреть, как интеграл используется при
- 4. Что такое интеграл и что значит интеграция и интегрирование? Выполнил студент группы 61 -11 Петров Данил
- 5. Значение слов в толковом словаре ИНТЕГРАЛ по Ефремовой: Интеграл - целая величина, рассматриваемая как сумма своих
- 6. ИНТЕГРИРОВАНИЕ Интегрирование - операция отыскания неопределенного интеграла (см.Интегральное исчисление) или решения дифференциального уравнения. Значение слова Интегрировать
- 7. ВЫПОЛНИЛИ СТУДЕНТЫ ГРУППЫ 61 -11 ЕФИМОВ ДМИТРИЙ КОРОТКЕВИЧ ЕВГЕНИЙ АНДРЕЙЧУК СЕРГЕЙ Немного истории
- 8. Определение Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции
- 9. Символ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма).
- 10. Интеграл в древности Возникновение задач интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого
- 11. Интеграл в древности Однако Архимед не выделил общего содержания интеграционных приемов и понятий об интеграле, а
- 12. История возникновения интеграла Труды Архимеда, впервые изданные в 1544 (на латинском и греческом языках), стали привлекать
- 13. История возникновения интеграла На такой кажущейся теперь по меньшей мере сомнительной основе И. Кеплер (1571 -
- 14. История возникновения интеграла В XVII веке были сделаны многие открытия, относящиеся к интегральному исчислению. Однако при
- 15. История возникновения интеграла Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам
- 16. История возникновения интеграла Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и
- 17. История возникновения интеграла Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать
- 18. История возникновения интеграла Строгое изложение теории интеграла появилось только в прошлом веке, Решение этой задачи связано
- 19. История возникновения интеграла Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены
- 20. История возникновения интеграла Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками
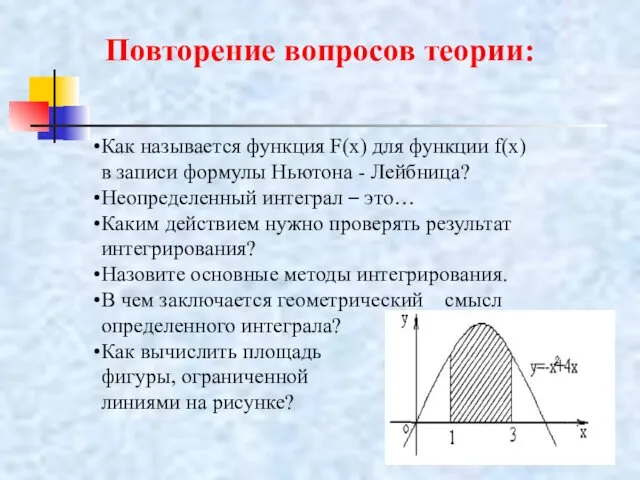
- 21. Повторение вопросов теории: Как называется функция F(x) для функции f(x) в записи формулы Ньютона - Лейбница?
- 22. Найти площадь заштрихованной фигуры
- 25. Какой метод интегрирования надо применить при вычисления интеграла ?
- 26. Решение – 5 минут На оценку 5 можно решить Непосредственное интегрирование – решить 4 примера или
- 27. Может ли современная наука обойтись без применения интегралов. В каких сферах современной науки применяется интеграл и
- 28. Применение определенного интеграла в физике Команда: Кодесников Владислав Гримович Никита Игнатьев Иван Воробьева Александра Андрейчук Сергей
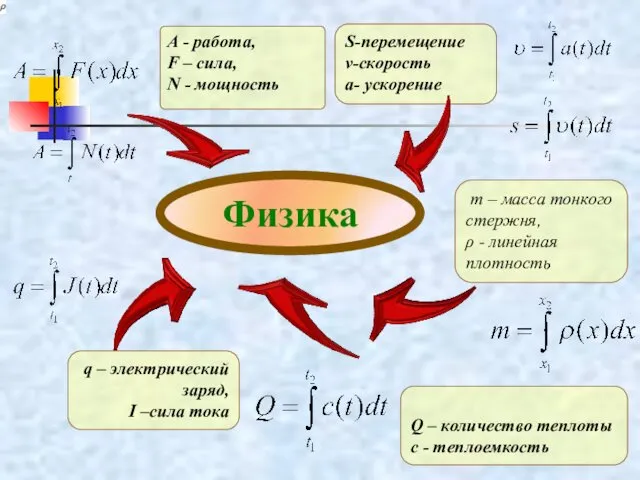
- 29. Применение интеграла ФИЗИКА Работа электрического заряда Работа переменной силы Масса Перемещение Давление Количество теплоты
- 30. S-перемещение v-скорость а- ускорение m – масса тонкого стержня, ρ - линейная плотность q – электрический
- 39. Задачи для самостоятельного решения Вычислите количество электричества, протекшего по проводнику за промежуток времени [ 2;3 ],
- 40. Применение определенного интеграла в биологии Команда Гуляева Евгения Голубева Валерия Ефимов Дмитрий Елина Дарина Иванов Даниил
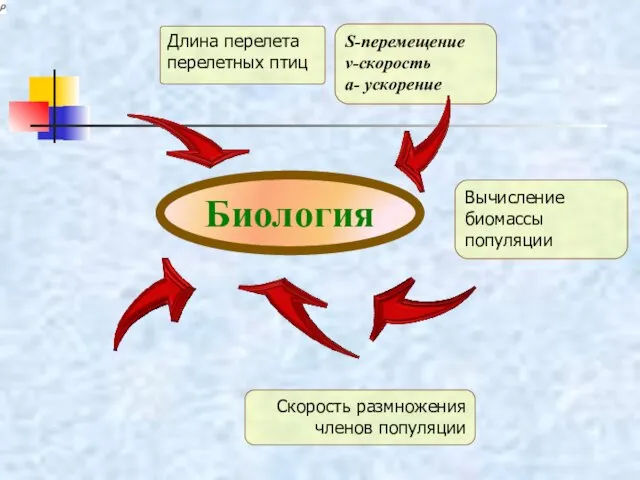
- 41. БИОЛОГИЯ Длина перелета перелетных птиц Биомасса популяции Скорость размножения членов популяции Численность популяции
- 42. S-перемещение v-скорость а- ускорение Вычисление биомассы популяции Скорость размножения членов популяции Биология Длина перелета перелетных птиц
- 43. Примеры решения задача 1 Количество зараженных в начальный момент времени 7 ч закон скорости заражения от
- 44. Задачи для самостоятельного решения Из эксперимента известно, что скорость размножения бактерий М = 5м +4 за
- 45. Применение определенного интеграла в экономике Команда Рейникова Алена Короткевич Евгений Бондарева Ольга Леонова Анастасия Артемьева Виктория
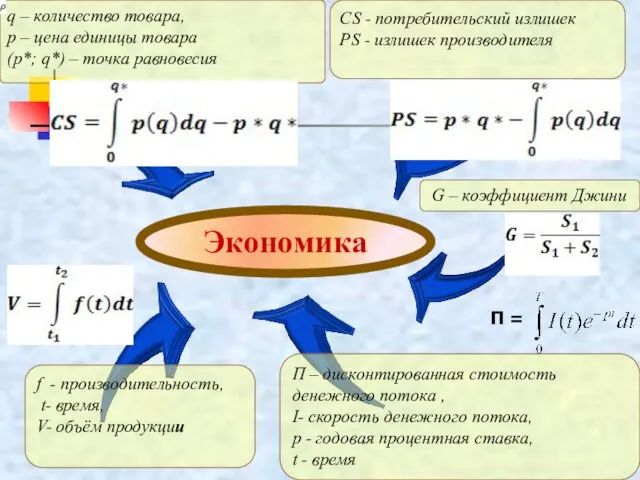
- 46. ЭКОНОМИКА Количество товара Производительность Объем продукции
- 47. СS - потребительский излишек PS - излишек производителя G – коэффициент Джини f - производительность, t-
- 48. Пример №1 Экспериментально установлено, что продуктивность труда работника приближенно выражается формулой: f (t) = -0,0033t²- 0,089t
- 49. Решение. Объем выпуска продукции в течение смены является первообразной для функции, выражающей продуктивность труда следовательно В
- 50. Пример №2 Экспериментально установлено, что зависимость расхода бензина автомобилем от скорости на 100 км, пути выражается
- 51. Задачи для самостоятельного решения 1. Определить объем продукции, произведенный рабочим за третий час рабочего дня, если
- 52. 2. Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией f(t)
- 53. Применение определенного интеграла в математике Команда Трофимов Анатолий Петров Даниил Калинкин Игорь Семенова Дарья Яковлева Диана
- 54. ГЕОМЕТРИЯ Площадь фигуры Объем тела вращения
- 55. Вычисление площади плоской фигуры в прямоугольных координатах Вычисление интеграла Вычисление площади поверхности тела вращения Математика Вычисление
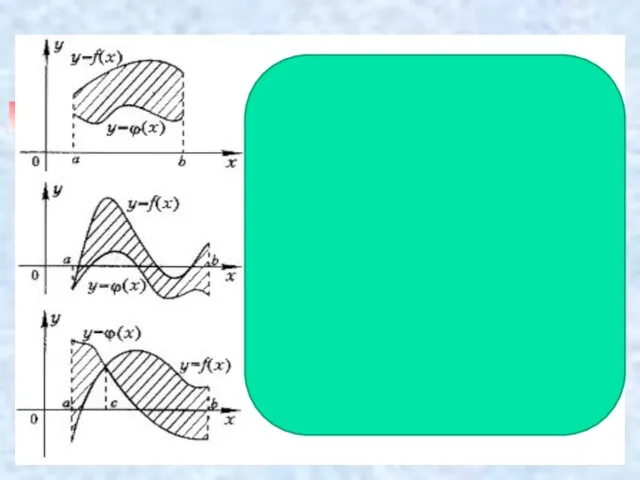
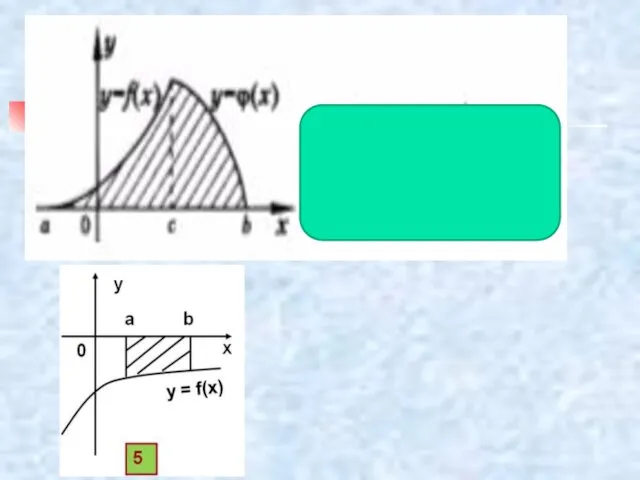
- 56. Фигуру, ограниченную графиком функции, отрезком [a;b] и прямыми x = a, x = b называют криволинейной
- 57. Задача №1 Вычислить площадь фигуры, ограниченной линиями 1 3 х у 0
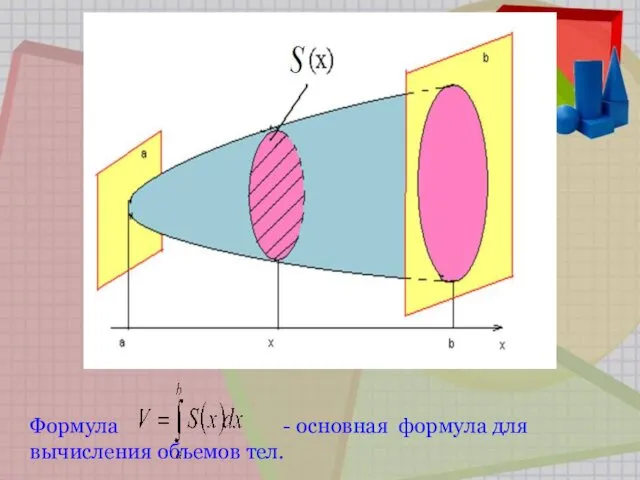
- 58. 2. Вычисление объёмов тел
- 59. Формула - основная формула для вычисления объемов тел.
- 60. Пусть вокруг оси OX вращается криволинейная трапеция, ограниченная непрерывной линией y = f(x) > 0, отрезком
- 61. Если криволинейная трапеция, ограниченная графиком функции x = q(y) > 0, прямыми y = c, y
- 62. Вычисление объема тела вращения Вычислить объем тела, образованного вращением фигуры, ограниченной линиями: вокруг оси OY.
- 63. Задача №2 Вычислить объем тела, образованного вращением одной арки синусоида (график функции y=sin x на промежутке
- 64. Решение задачи №2
- 65. Применяя определенный интеграл можно вывести ряд формул объемов стереометрических фигур Объем шара:
- 66. Объем конуса
- 67. Задачи для самостоятельного решения Найти объём усечённого конуса, образованного вращением прямой y = x + 1
- 68. Практическая работа. Вычислить объем тела образованного вращением вокруг оси Ох, ограниченного указанными линиями у = х2-9
- 69. Уже Архимед успешно находил площади фигур, несмотря на то, что в математике его времени не было
- 70. Мини- тест. Задания для студентов на оценку «3» №1. С помощью формулы Ньютона- Лейбница вычисляют: а)
- 71. Задания для студентов на оценку «4» и «5» №1.Вычислите Ответы: а) ; б) ; в) ;
- 72. Заключение Применение физических моделей при введении понятия интеграла, рассмотрении его свойств, отработке техники интегрирования и изучении
- 73. Спасибо за внимание ☺
- 75. Скачать презентацию




























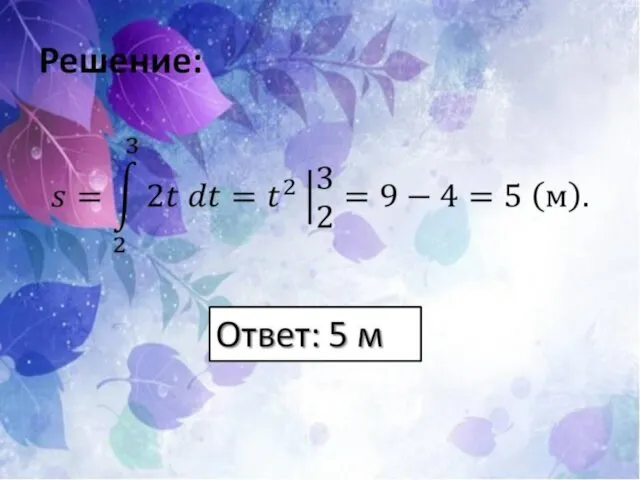



















![Фигуру, ограниченную графиком функции, отрезком [a;b] и прямыми x =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/94060/slide-55.jpg)
















 Взаємне розміщення площини і кулі у просторі
Взаємне розміщення площини і кулі у просторі Благоприятствующие элементарные события. Вероятность события
Благоприятствующие элементарные события. Вероятность события Решение систем уравнений с двумя неизвестными
Решение систем уравнений с двумя неизвестными Урок математики 1класс. Точки и линии
Урок математики 1класс. Точки и линии Теоретическая модель жизни пчелиных колоний
Теоретическая модель жизни пчелиных колоний Оригами как метод ознакомления детей с формой предметов.
Оригами как метод ознакомления детей с формой предметов. Презентация-игра Помогите сказке
Презентация-игра Помогите сказке Математика. 1 класс. Урок 55. Числа 0-10 - Презентация
Математика. 1 класс. Урок 55. Числа 0-10 - Презентация Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Задачи теории вероятностей. Повторение к ГИА и ЕГЭ
Задачи теории вероятностей. Повторение к ГИА и ЕГЭ Алгоритм сложения трёхзначных чисел
Алгоритм сложения трёхзначных чисел Столбчатые диаграммы. Демонстрационный материал. 6 класс
Столбчатые диаграммы. Демонстрационный материал. 6 класс Основы математической обработки информации
Основы математической обработки информации Теорема Виета
Теорема Виета Следствие из аксиом стереометрии
Следствие из аксиом стереометрии Десятичные дроби. 5 класс
Десятичные дроби. 5 класс Рациональные уравнения как математические модели реальных ситуаций
Рациональные уравнения как математические модели реальных ситуаций Подобие в геометрии. Подобные треугольники
Подобие в геометрии. Подобные треугольники Прямоугольный параллелепипед
Прямоугольный параллелепипед Деление с остатком
Деление с остатком Доказательство теоремы Пифагора
Доказательство теоремы Пифагора Топологические объекты
Топологические объекты Основы векторной алгебры. Векторы на плоскости и в пространстве
Основы векторной алгебры. Векторы на плоскости и в пространстве Целеполагание как этап современного урока в условиях ФГОС
Целеполагание как этап современного урока в условиях ФГОС Урок математики 1 класс Тема: Число восемь. Цифра 8.
Урок математики 1 класс Тема: Число восемь. Цифра 8. ОГЭ Модуль Реальная математика
ОГЭ Модуль Реальная математика Геометрична фігура трикутник. (7 класс)
Геометрична фігура трикутник. (7 класс) Конспект урока математики 2 класс по системе Занкова (И.И.Аргинская) Тема урока: Умножение
Конспект урока математики 2 класс по системе Занкова (И.И.Аргинская) Тема урока: Умножение