Содержание
- 2. Введение Математика – наука о количественных отношениях и пространственных формах действительного мира (Фридрих Энгельс). Математика –
- 3. Разделы современной математики Сегодня в математике обычно выделяют следующие области: математический анализ дифференциальные уравнения уравнения с
- 4. Аксиоматический подход в математике В основе построения математической теории лежит аксиоматический метод. В основу научной теории
- 5. Математика на стыке наук математическая физика, математическая логика, математическая лингвистика, математическая экономика, математическая история и др.
- 6. Математика в естествознании Направления в изучении объектов окружающего мира (направления познания): Экспериментальное Теоретическое Вычислительное
- 7. Экспериментальное направление Наблюдение Эксперимент Математическая обработка результатов эксперимента (экспериментальных данных) определение истинных значений измеряемых величин определение
- 8. Теоретическое направление Выдвижение гипотезы и построение математической модели (в виде уравнений или неравенств) Исследование математической модели
- 9. Вычислительное направление Выбор или построение математической модели Разработка численного алгоритма решения математической задачи Составление компьютерной программы
- 10. Математическое моделирование Модель – это такой материальный или мысленно представленный объект, который в процессе познания (изучения)
- 11. Основные этапы математического моделирования Построение модели. На этом этапе задается некоторый «нематематический» объект — явление природы,
- 12. Математический язык Математика: мышление, чувствование и язык. Язык – это система условных знаков, принятых в некотором
- 13. Математический язык (продолжение) Язык в широком смысле – это словарь, грамматика, рассказы, повести, пьесы и романы,
- 14. Элементы теории множеств Множество – первичное понятие современной математики, это понятие не определяется через другие понятия
- 15. Элементы теории множеств (продолжение) Множества, состоящие из конечного числа элементов – конечные множества Множества, состоящие из
- 16. Элементы теории множеств (продолжение) Обозначения: Объект х есть элемент множества Х Объект х не принадлежит множеству
- 17. Элементы теории множеств (продолжение) Числовые множества Множество натуральных чисел Множество целых чисел Множество рациональных чисел Q
- 18. Элементы теории множеств (продолжение) Упражнения: Какие из следующих множеств геометрических фигур на плоскости равны между собой:
- 19. Алгебраические операции над множествами Объединением множеств A и B называется новое множество, которое обозначается A∪B и
- 20. Алгебраические операции над множествами Разностью множеств A и B называется новое множество, которое обозначается A\B и
- 21. Алгебраические операции над множествами Декартовым произведением множеств A и B называется новое множество, обозначаемое A×B, элементами
- 22. Алгебраические операции над множествами. Круги Эйлера или диаграммы Венна.
- 23. Алгебраические операции над множествами. Круги Эйлера или диаграммы Венна.
- 24. Алгебраические операции над множествами Упражнения Выпишите все подмножества множества В = {1, 2, 3} Запишите множество
- 25. Численность множества Пусть A и B – конечные множества. Число элементов множества A условимся обозначать символом
- 26. Использование теории множеств для решения задач Задача 1 В группе 40 студентов. Из них 23 любят
- 27. Использование теории множеств для решения задач Задача 2 В группе из 100 туристов 70 человек знают
- 28. Использование теории множеств для решения задач Задача 3 20 мальчиков поехали на пикник. При этом 5
- 29. Элементы дискретной математики Элементы комбинаторики Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько
- 30. Элементы комбинаторики Основные правила комбинаторики Правило сложения Из пункта А в пункт Б можно добраться: самолетом
- 31. Основные правила комбинаторики Правило умножения Если элемент A можно выбрать n способами и, при любом выборе
- 32. Основные правила комбинаторики Правило умножения (пример) 1) 3) 5) 6) 2 · 3 = 6 способов
- 33. Элементы комбинаторики Размещения Пусть дано множество, состоящее из n элементов. Размещением из n элементов по k
- 34. Основные правила комбинаторики Число размещений (пример)
- 35. Элементы комбинаторики Перестановки Пусть дано множество, состоящее из n элементов. Перестановкой из n элементов называется размещение
- 36. Основные правила комбинаторики Число перестановок (пример)
- 37. Элементы комбинаторики Сочетания Пусть дано множество, состоящее из n элементов. Сочетанием из n элементов по k
- 38. Основные правила комбинаторики Число сочетаний (пример)
- 39. Элементы комбинаторики Упражнения Имеется 5 видов конвертов без марок и 4 вида марок. Сколькими способами можно
- 40. Элементы комбинаторики Задача на комбинированную выборку Задача: В колоде – 36 карт: четыре масти по девять
- 41. Элементы комбинаторики Возможные ошибки Задача: Сколько существует вариантов выбрать шесть карт из колоды (36 карт) так,
- 42. Элементы комбинаторики Задания на дом: 1) Составить таблицу 2) Придумать задачи
- 43. Элементы математической логики Логика – это наука о формах и законах правильного мышления. Она появилась приблизительно
- 44. Элементы математической логики По содержанию человеческое мышление бесконечно многообразно, но форм, в которых выражается это разнообразие,
- 45. Элементы математической логики Высказывание – любое повествовательное предложение, о котором можно сказать истинно оно или ложно
- 46. Элементы математической логики
- 47. Основные логические операции Например для высказывания «Волга впадает в Балтийское море» отрицанием будет высказывание : «Неверно,
- 48. Основные логические операции
- 49. Основные логические операции
- 50. Основные логические операции
- 51. Основные логические операции
- 52. Основные логические операции
- 53. Основные логические операции Упражнения:
- 54. Основные логические операции Таблицы истинности Таблица истинности для логического отрицания имеет вид: Логические значения остальных операций
- 55. Формулы алгебры логики
- 56. Формулы алгебры логики
- 57. Формулы алгебры логики Упражнение:
- 58. Использование таблиц истинности Например: Составить таблицу истинности для формулы:
- 59. Использование таблиц истинности
- 60. Равносильности алгебры логики
- 61. Равносильности алгебры логики
- 62. Решение логических задач
- 63. Решение логических задач
- 64. Табличный метод решение задач Табличный метод решения логических задач весьма удобен при установлении истинности одного из
- 65. Табличный метод решение задач Решение. Обозначим через I высказывание «Виноват Иванов», P — «Виноват Петров», S
- 66. Табличный метод решение задач
- 67. Основы теории вероятностей Теория вероятностей – раздел математики, в котором изучаются закономерности, присущие массовым случайным явлениям.
- 68. Основные понятия теории вероятностей Понятие о случайном событии Опыт, эксперимент, наблюдение, повторяемое многократно называют испытанием. Например:
- 69. Основные понятия теории вероятностей Определение. Два события называются совместными, если появление одного из них не исключает
- 70. Основные понятия теории вероятностей Определение вероятности Вероятность события А – число Р(А), характеризующее возможность появления этого
- 71. Основные понятия теории вероятностей Алгебра событий Определение. Суммой событий А и В называется событие С =
- 72. Основные понятия теории вероятностей Теорема сложение вероятностей Если события А и В – несовместные, то вероятность
- 73. Основы теории вероятностей Примеры задач на подсчет вероятностей Игральную кость подбрасывают три раза. Какова вероятность того,
- 74. Случайная величина (СВ) – величина, которая в результате опыта принимает одно заранее неизвестное значение Примеры: количество
- 75. Виды случайных величин (СВ) Дискретные СВ (ДСВ) – СВ, значения которых можно пересчитать (например: число звонков
- 76. Закон распределения СВ Основная задача теории вероятностей, оперирующей случайными величинами, – это определение закона распределения случайной
- 77. Числовые характеристики СВ Математическое ожидание М(Х) – это центральная точка, вокруг которой рассеяны все значения случайной
- 79. Дисперсия
- 80. Среднее квадратическое отклонение
- 81. Основные понятия математической статистики (МС) Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации
- 82. Генеральная совокупность – совокупность всех объектов, подлежащих изучению. Сплошное наблюдение – изучение всех объектов генеральной совокупности.
- 83. Варианта (хi ) – наблюдаемое значение Частотота (ni ) - число наблюдений значения Относительная частота (ni
- 84. Описательная статистика Меры центральной тенденции Мода (Mo) – наиболее часто встречающееся значение в ряду данных. Выборка
- 85. Среднее арифметическое значение – отношение суммы всех значений изучаемого признака к числу слагаемых.
- 87. Медиана (Ме)– разбивает ряд на две равные части. Для определения медианы сначала ряд упорядочивают (записывают в
- 88. Меры изменчивости Размах - разница между максимальным и минимальным значениями. Дисперсия – мера разброса данных относительно
- 90. Первичное описание исходных данных Вариационный ряд – таблица, отражающая зависимость между видами исходов проводимого опыта и
- 94. Скачать презентацию
 Оптимізаційні методи та моделі. Нелінійні задачі оптимізації. Постановка задачі, графічний метод. (Тема 11)
Оптимізаційні методи та моделі. Нелінійні задачі оптимізації. Постановка задачі, графічний метод. (Тема 11) Свойства деления
Свойства деления Площади фигур
Площади фигур Удивительные десятичные дроби. 5 класс
Удивительные десятичные дроби. 5 класс Рівняння дотичної до графіка функції
Рівняння дотичної до графіка функції Что такое задача (презентация к уроку)
Что такое задача (презентация к уроку) Тоновое решение, акценты эскизов. Линия, пятно и линия, пятно
Тоновое решение, акценты эскизов. Линия, пятно и линия, пятно Прогулка в Простоквашино
Прогулка в Простоквашино Kristālisko vielu ārējā (formas) simetrija
Kristālisko vielu ārējā (formas) simetrija Среднее арифметическое. Урок-сказка
Среднее арифметическое. Урок-сказка Деление трехзначного числа на однозначное
Деление трехзначного числа на однозначное ЕГЭ по математике. Вариант 1
ЕГЭ по математике. Вариант 1 Решение уравнения Cos x=a
Решение уравнения Cos x=a Презентация поматематике
Презентация поматематике Прямая и обратная пропорциональные зависимости. (6 класс)
Прямая и обратная пропорциональные зависимости. (6 класс) Логика высказываний
Логика высказываний Призма. Площадь и объем
Призма. Площадь и объем Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Теория комплексных чисел. Показательная форма комплексного числа. (Тема 4)
Теория комплексных чисел. Показательная форма комплексного числа. (Тема 4) Прямая и кривая линии. (1 класс)
Прямая и кривая линии. (1 класс) Решето Эратосфена
Решето Эратосфена 20231001_1._ponyatie_vektora_v_prostranstve
20231001_1._ponyatie_vektora_v_prostranstve Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы История возникновения треугольника
История возникновения треугольника Производная. Устные упражнения
Производная. Устные упражнения Натуральные числа. 7 класс
Натуральные числа. 7 класс Решение задач по теме Исследование функции с помощью производной
Решение задач по теме Исследование функции с помощью производной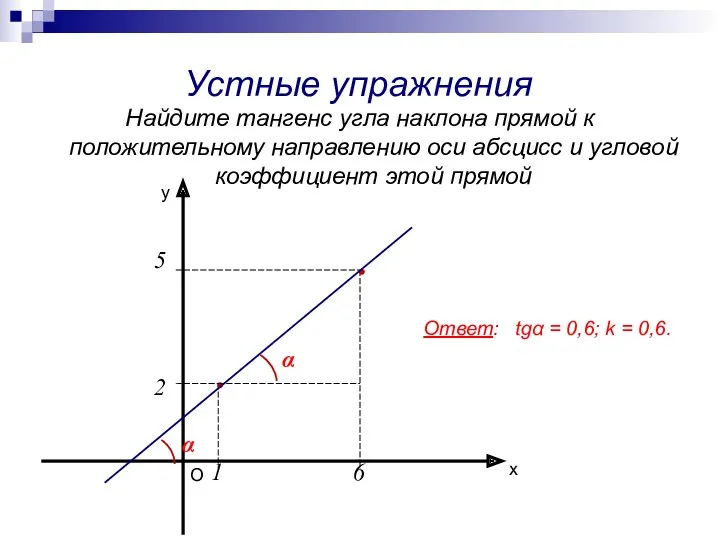 Устные упражнения. Определение производной. (10 класс)
Устные упражнения. Определение производной. (10 класс)