Содержание
- 2. Матвейчук Наталья Михайловна, к.ф.-м.н., доцент кафедры ЭИ, ауд. 804-5(кафедра), 801а-5 (44)700-91-83, (29)740-11-63 matsveichuk@tut.by
- 3. ТЕМЫ: Задачи нелинейного и целочисленного линейного программирования Модели управления запасами Динамическое программирование Оптимизационные задачи на графах
- 4. Теория игр Джон Нэш – 1994 (экономика) Элвин Рот и Ллойд Шепли – 2012 (экономика) Теория
- 5. ЗАДАЧА НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
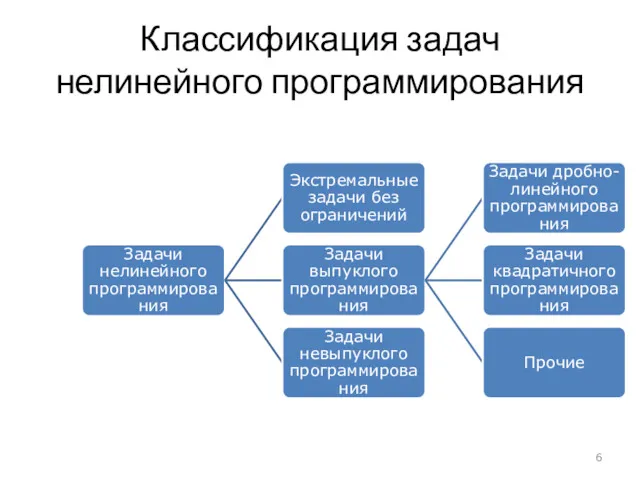
- 6. Классификация задач нелинейного программирования
- 7. Экстремальная задача без ограничений: случай одной переменной Постановка задачи: y = f(x) → max (min) Необходимое
- 8. Экстремальная задача без ограничений: случай двух переменных Постановка задачи: z = f(x, y) → max (min)
- 9. Экстремальная задача без ограничений: случай двух переменных Достаточные условия экстремума в точке (x0, y0): обозначим частные
- 10. Экстремальная задача без ограничений: общий случай Постановка задачи: Необходимое условие экстремума в точке (Х0 – стационарная
- 11. Экстремальная задача без ограничений: общий случай Достаточные условия экстремума в точке Х0: Если матрица вторых частных
- 12. Матрица Гессе:
- 13. Матрица Гессе является матрицей квадратичной формы относительно приращений Δx1, Δx2,…, Δxn. Матрица положительно (отрицательно) определена (полу),
- 14. Критерий Сильвестра (устанавливает определенность квадратичной формы): квадратичная форма положительно определена тогда и только тогда, когда все
- 15. Порядок решения: найти частные производные первого порядка и приравнять к нулю; решить полученную систему, найти стационарные
- 16. Пример. Квадратичная функция ⇒
- 17. Пример. Квадратичная функция Матрица Гессе: Точка (0, 0) – точка максимума
- 18. Отличия от ЗЛП: 1. ОДЗ не обязательно выпуклая. 2. Экстремум не обязан находится на границе ОДЗ.
- 19. Геометрически задача НП состоит в отыскании точки или множества точек из допустимого множества, где достигается поверхность
- 20. Пример: Найти экстремумы функции L(x1,x2)=x1+2x2 при ограничениях x12 + x22 ≤ 25, x1 ≥ 0, x2
- 21. Пример: Максимум достигается в точке пересечения ограничений 2 и 3: Минимум достигается в центре окружности:
- 22. Пример:
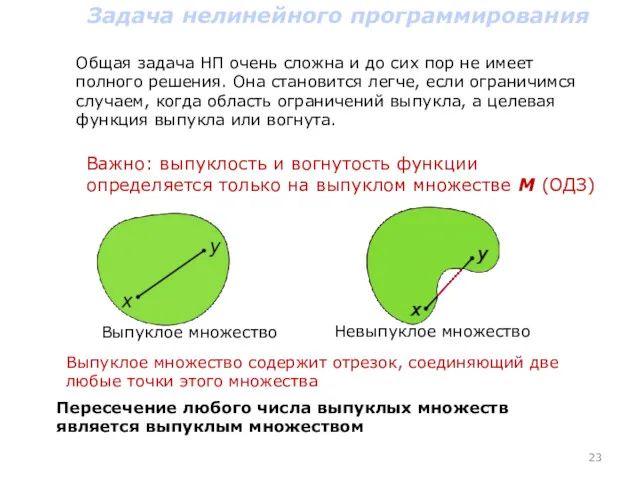
- 23. Задача нелинейного программирования Общая задача НП очень сложна и до сих пор не имеет полного решения.
- 24. Повторение Функция f(x) является выпуклой, если для любых х1, х2 и положительных α, β, в сумме
- 25. ПРИЗНАК СТРОГОЙ ВЫПУКЛОСТИ Дважды дифференцируемая функция f(X) = f(x1, …, хn ) является выпуклой в том
- 26. f(x1,x2, …,хn) – выпуклая на М f(x1,x2, …,хn) – вогнутая на М gi(x1,x2, …,хn) - выпуклые
- 27. Свойства выпуклых функций: 1) Если f(X) – выпукла, то функция - f(X) – вогнута. 2) Линии
- 28. Теорема Вейерштрасса: если функция f непрерывна на компакте (ограниченном и замкнутом множестве), то она достигает минимума
- 29. Если целевая функция f является строго выпуклой (строго вогнутой) и если область решений системы ограничений не
- 30. Свойства строго выпуклых функций: - строго выпуклая функция f имеет не больше одного локального минимума на
- 31. Решение любой задачи математического программирования (в том числе нелинейного) можно свести к решению задачи нелинейного программирования
- 32. Метод неопределенных множителей Лагранжа Задача нелинейного программирования с ограничениями-равенствами: (m Составим функцию Лагранжа: Введем вектор-строку из
- 33. Принцип Лагранжа (необходимое условие экстремума) причем все gi непрерывно дифференцируемы в окрестности этой точки, и векторы
- 34. Применим необходимое условие экстремума функции
- 35. Решив полученную систему уравнений, найдем вектор Из стационарных точек, взятых без координат λ1,…,λm, выберем точки, в
- 36. Задача По плану производства продукции предприятию необходимо изготовить 180 изделий. Они могут быть изготовлены двумя способами.
- 37. Интерпретация множителей Лагранжа Помимо того, что метод Лагранжа дает решение задачи на максимум, он позволяет также
- 38. Экономическая интерпретация множителей Лагранжа, соответствующих оптимальному решению, аналогична интерпретации двойственных оценок ограничений ЗЛП Они показывают величину
- 39. Чтобы применить метод неопределенных множителей Лагранжа, ограничения-неравенства преобразуем к виду равенств путем введения дополнительных неотрицательных переменных
- 40. Необходимым условием оптимальности является неотрицательность вектора Действительно, как было показано, Но при увеличении b допустимое множество
- 41. Применим необходимое условие экстремума функции Из двух последних выражений имеем Если λi>0, то si=0 и bi
- 42. С учетом неотрицательности вектора и условия Получаем условие дополняющей нежесткости
- 43. Условия Куна-Таккера (необходимые условия экстремума в задаче с ограничениями-неравенствами):
- 44. Аналогично предыдущему ограничения-неравенства преобразуем к виду равенств путем введения дополнительных неотрицательных переменных s=(s1,…,sm) и t=(t1,…,tn). Задача
- 45. (m Введем множители Лагранжа λ=(λ1,…,λm) и μ=(μ1,…, μn) Составим функцию Лагранжа: Перепишем задачу в виде
- 46. Запишем условия Куна-Таккера: Исключив из этих уравнений μ, получим
- 47. Условия Куна-Таккера: В случае задачи минимизации знаки неравенств в первой и последнем из этих условий заменяются
- 48. Теорема Куна-Таккера любой из существующих оптимумов функции f соответствует точке Куна-Таккера функции Лагранжа Если функция f
- 50. Скачать презентацию













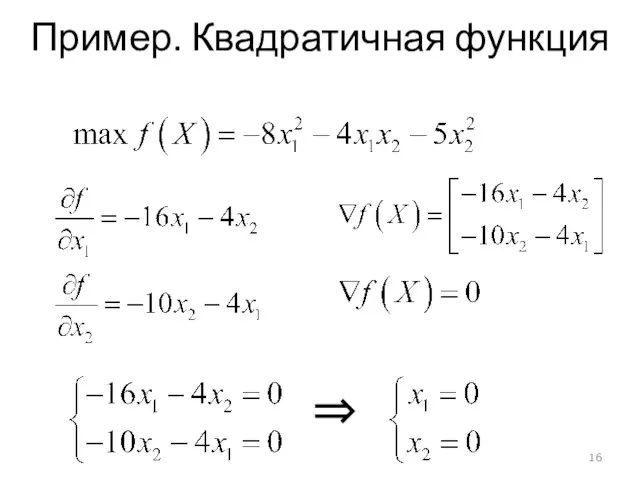































 Понятие линейного динамического звена. Лекция 2
Понятие линейного динамического звена. Лекция 2 Григорий Яковлевич Перельман
Григорий Яковлевич Перельман Головоломки со спичками
Головоломки со спичками Натуральные числа. Задачи на движение
Натуральные числа. Задачи на движение Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб
Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб Балансовые модели
Балансовые модели Своя игра. Устный счёт
Своя игра. Устный счёт График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Сложение и вычитание двузначных чисел
Сложение и вычитание двузначных чисел Презентация Игры с геометрическими фигурами для детей 3-4 лет
Презентация Игры с геометрическими фигурами для детей 3-4 лет Решение региональных задач. Ставропольский край
Решение региональных задач. Ставропольский край Деятельность учителя в условиях реализации ФГОС
Деятельность учителя в условиях реализации ФГОС Умножение десятичных дробей
Умножение десятичных дробей ЕГЭ - профиль №15. 2018 год
ЕГЭ - профиль №15. 2018 год Задания на развитие логического мышления
Задания на развитие логического мышления Рабочая учебная программа развития логического мышления у детей 6 – 7 лет на основе занимательной математики Логика
Рабочая учебная программа развития логического мышления у детей 6 – 7 лет на основе занимательной математики Логика Активізація розумової діяльності та розвиток творчості на уроках математики. Творчий звіт
Активізація розумової діяльності та розвиток творчості на уроках математики. Творчий звіт Прогрессии вокруг нас
Прогрессии вокруг нас Концентрация, смеси и сплавы
Концентрация, смеси и сплавы Прямоугольный треугольник. 7 класс
Прямоугольный треугольник. 7 класс Презентация по математике по теме Задачи на движение4 класс
Презентация по математике по теме Задачи на движение4 класс III городской турнир по ментальной арифметике
III городской турнир по ментальной арифметике Призма. Площадь и объем
Призма. Площадь и объем Презентация по математике Деление на трехзначное число
Презентация по математике Деление на трехзначное число Комбинаторные задачи. Комбинаторика
Комбинаторные задачи. Комбинаторика Урок 10. Случайные величины. Дискретные и непрерывные случайные величины (ДСВ и НСВ)
Урок 10. Случайные величины. Дискретные и непрерывные случайные величины (ДСВ и НСВ) Параллельный перенос в пространстве
Параллельный перенос в пространстве