Содержание
- 2. Определение Комплексным числом называется число вида где , а x и y – вещественные числа.
- 3. Основная теорема алгебры Выражение называется алгебраической формой записи комплексного числа.
- 4. Число x называется действительной частью, y–мнимой частью комплексного числа z. Это записывают следующим образом:
- 5. Если , то число называют чисто мнимым. Если , то получается вещественное число. Два комплексных числа
- 6. Два комплексных числа и равны друг другу, если и Комплексное число z считается равным нулю, если
- 7. Всякое комплексное число можно изобразить точкой на плоскости, т.к. каждому z соответствует упорядоченная пара вещественных чисел
- 8. Число z=0 ставится в соответствие началу координатной плоскости. Такую плоскость мы в дальнейшем будем называть комплексной
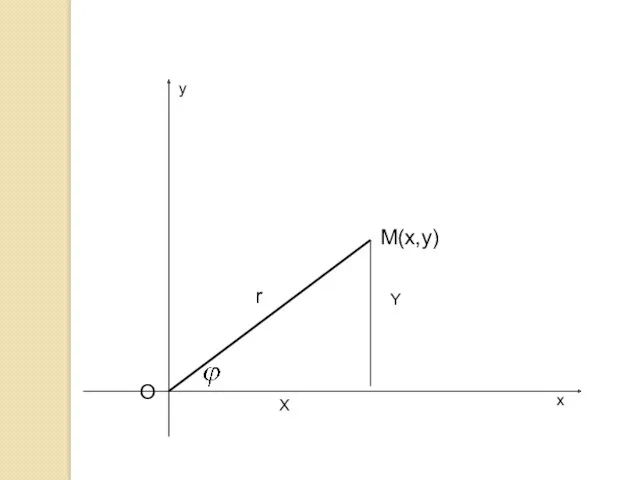
- 9. O M(x,y) X Y r х у
- 10. Модуль комплексного числа Число называется модулем комплексного числа и обозначается .
- 11. Тригонометрическая и показательная формы комплексного числа Для определения положения точки на плоскости можно пользоваться полярными координатами
- 12. Положительным направлением изменения угла φ считается направление против часовой стрелки. Воспользовавшись связью декартовых и полярных координат:
- 13. , φ – аргумент комплексного числа, который находят из формул или в силу того, что ,
- 14. Пример Записать в тригонометрической форме комплексное число Очевидно точка находится во 2-й четверти и поэтому .
- 15. Имеем .
- 16. Показательная форма комплексного числа Используя формулу Эйлера , получаем показательную форму записи комплексного числа
- 17. Действия над комплексными числами
- 18. Действия над комплексными числами
- 19. Действия над комплексными числами
- 20. Действия над комплексными числами
- 22. Формула Муавра
- 23. Извлечение корня В тригонометрической форме корень n–й степени вычисляют по формуле: а в показательной – по
- 24. Пример . Возвести число в пятую степень.
- 25. Тогда по формуле Муавра получим
- 27. Найти .
- 29. Скачать презентацию












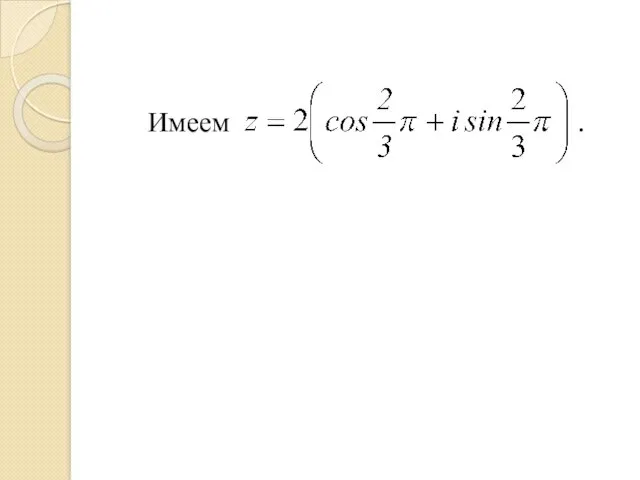

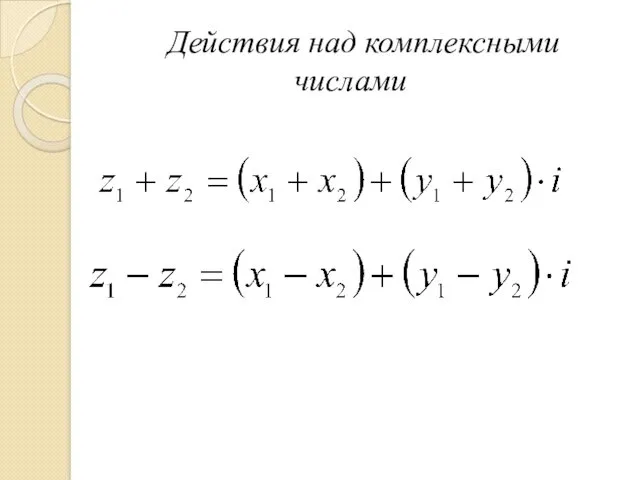



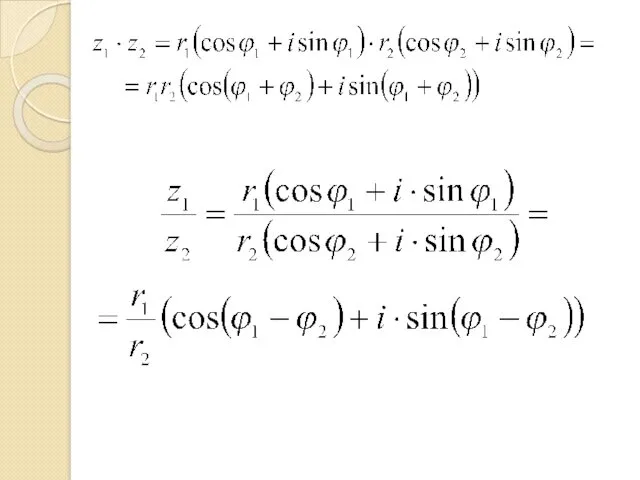
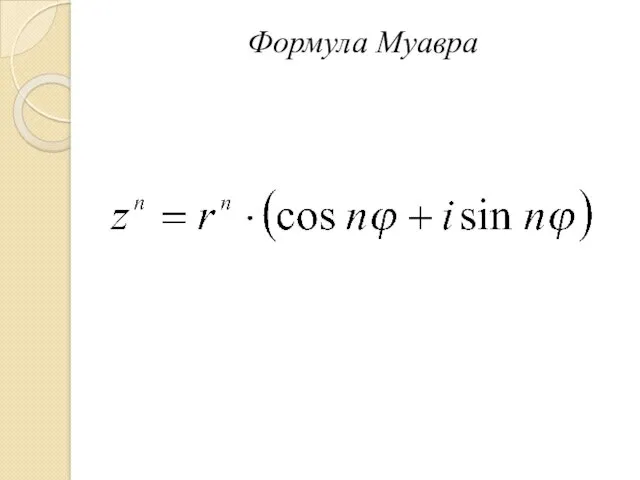



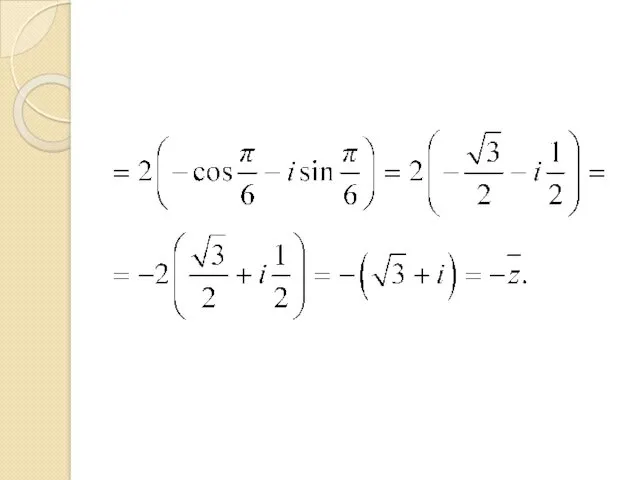
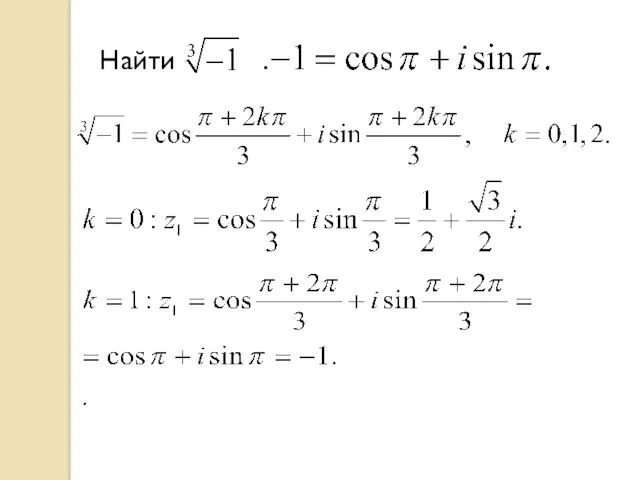
 Занимательные задачи по наглядной геометрии
Занимательные задачи по наглядной геометрии Великая Победа в математических задачах (5 класс)
Великая Победа в математических задачах (5 класс) Неравенства
Неравенства Презентация Угостим гостью. (Деление предмета на две равные части).
Презентация Угостим гостью. (Деление предмета на две равные части). Решение логарифмических уравнений и неравенств
Решение логарифмических уравнений и неравенств Метод поиска гармонии
Метод поиска гармонии Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Соотношение единиц площади.
Соотношение единиц площади. Правильные и неправильные дроби
Правильные и неправильные дроби Теорема Пифагора
Теорема Пифагора Занимательная математика
Занимательная математика Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа. Урок 6
Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа. Урок 6 Решение текстовых задач при подготовке к ЕГЭ и ГИА
Решение текстовых задач при подготовке к ЕГЭ и ГИА Презентация для учащихся 2 класса по математике (автор Л.Г. Петерсон) Такая загадочная Индия
Презентация для учащихся 2 класса по математике (автор Л.Г. Петерсон) Такая загадочная Индия Построение сечений в тетраэдре и параллелепипеде
Построение сечений в тетраэдре и параллелепипеде Відомі математики
Відомі математики Круги Эйлера
Круги Эйлера Двугранный угол
Двугранный угол Занимательная арифметика
Занимательная арифметика Множества. Понятие множества
Множества. Понятие множества Среднее арифметическое
Среднее арифметическое Алгоритм вычитания трёхзначных чисел. 3 класс
Алгоритм вычитания трёхзначных чисел. 3 класс Степень с натуральным показателем. Устный опрос
Степень с натуральным показателем. Устный опрос Мир геометрии
Мир геометрии Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Касательная к графику функции
Касательная к графику функции Функции y = tgx и y = ctgx, их свойства и графики
Функции y = tgx и y = ctgx, их свойства и графики Линейная функция и её график. Устная работа
Линейная функция и её график. Устная работа