Содержание
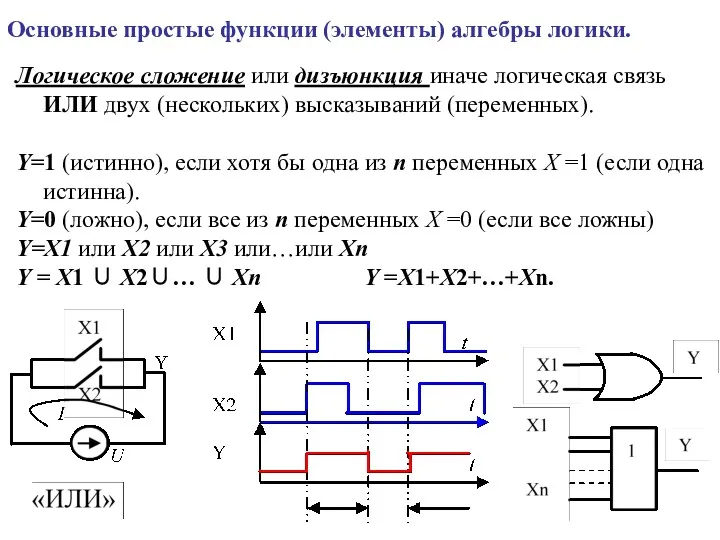
- 2. Логическое сложение или дизъюнкция иначе логическая связь ИЛИ двух (нескольких) высказываний (переменных). Y=1 (истинно), если хотя
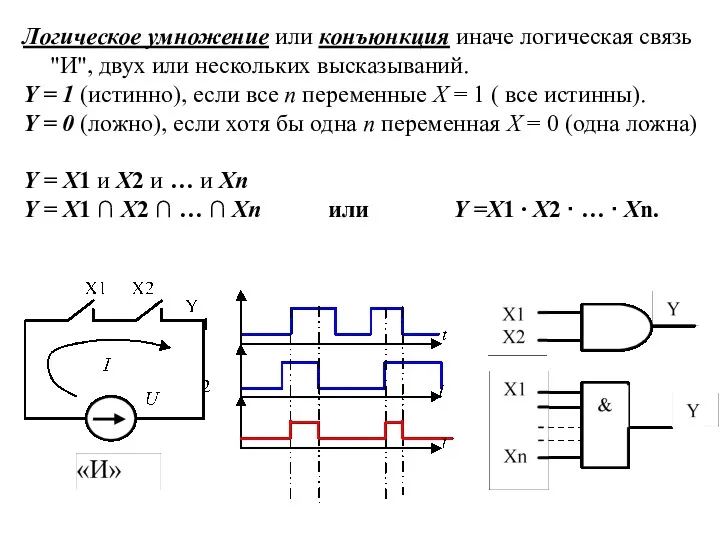
- 3. Логическое умножение или конъюнкция иначе логическая связь "И", двух или нескольких высказываний. Y = 1 (истинно),
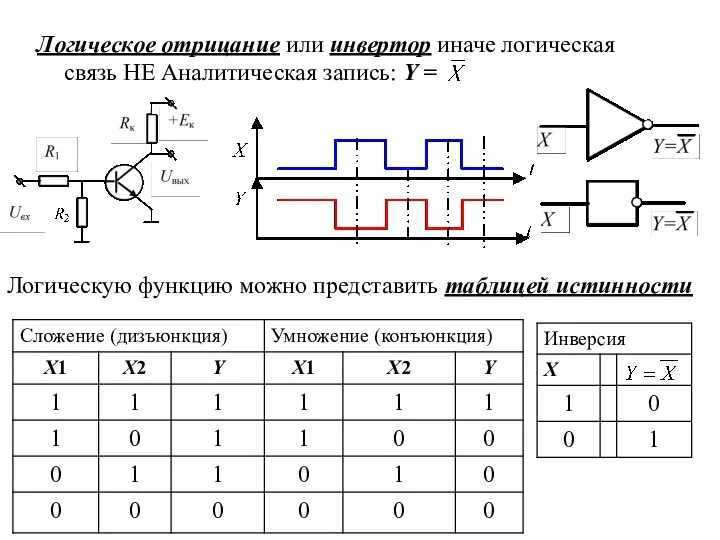
- 4. Логическое отрицание или инвертор иначе логическая связь НЕ Аналитическая запись: Y = Логическую функцию можно представить
- 5. Свойства переключательных функций. Функции вида Y=f(x1, x2,…xn) называется переключательной функцией ПФ. ПФ могут быть представлена: аналитически
- 6. Основные законы алгебры логики (АЛ). В АЛ есть 4 основных закона, которые устанавливают эквивалентность логических функций
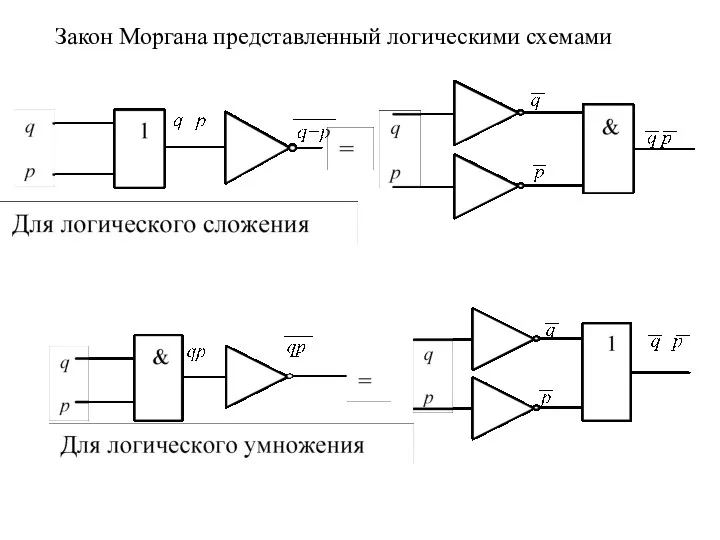
- 7. Закон Моргана представленный логическими схемами
- 8. Аксиомы для одной логической переменной. Всегда справедливо для логического: сложения умножения p + 1 = 1
- 9. Теоремы поглощения для-2х переменных: p + р × q = p; p(р +q) = p; p
- 10. Проектирование логических устройств Y1 = f(x1,x2,x3) Y2 = f(x1,x2,x3) Y3 = f(x1,x2,x3) Логическое устройство задается в
- 11. Совершенные нормальные формы представления ЛФ ЛФ всегда можно представить в виде: суммы произведений переменных, произведения сумм
- 12. Комбинации переменных для которых У=1 называются конституентами единицы или минтермами. Сумма минтерм и определяет ее СНДФ:
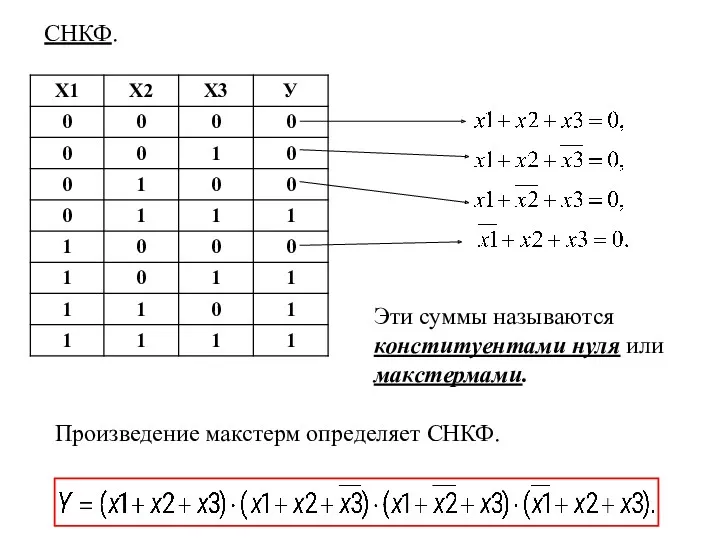
- 13. Эти суммы называются конституентами нуля или макстермами. СНКФ. Произведение макстерм определяет СНКФ.
- 14. По теореме склеивания СНДФ СНКФ И по теореме склеивания для 3-х переменных: (p + q) (p
- 16. Примеры преобразования заданных ЛФ к более простым выражениям используя законы и аксиомы АЛ. Теорема поглощения Закон
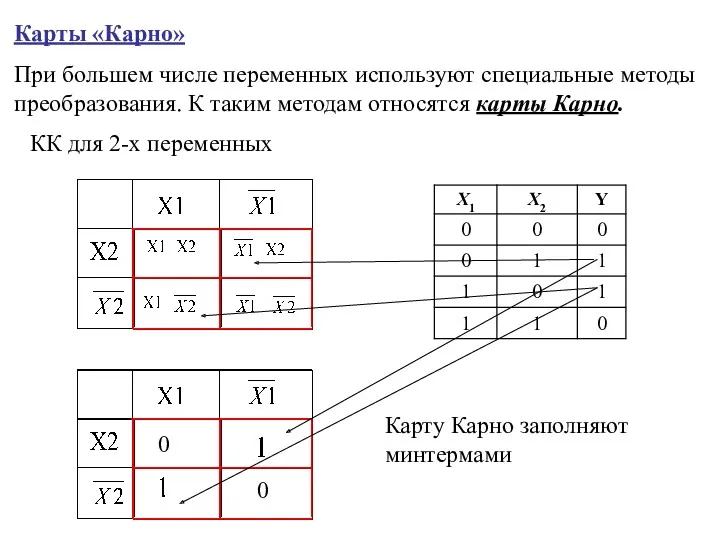
- 17. Карты «Карно» При большем числе переменных используют специальные методы преобразования. К таким методам относятся карты Карно.
- 18. Для 3-х переменных Правило для составления КК. Соседние ячейки могут отличаться только на один элемент, который
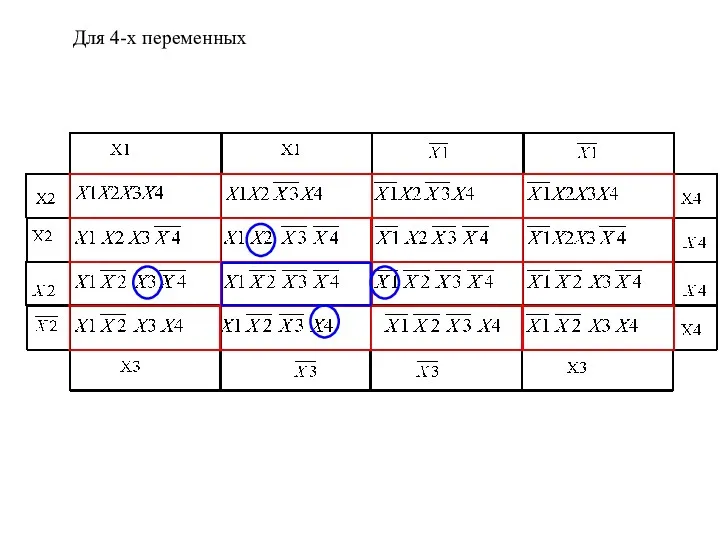
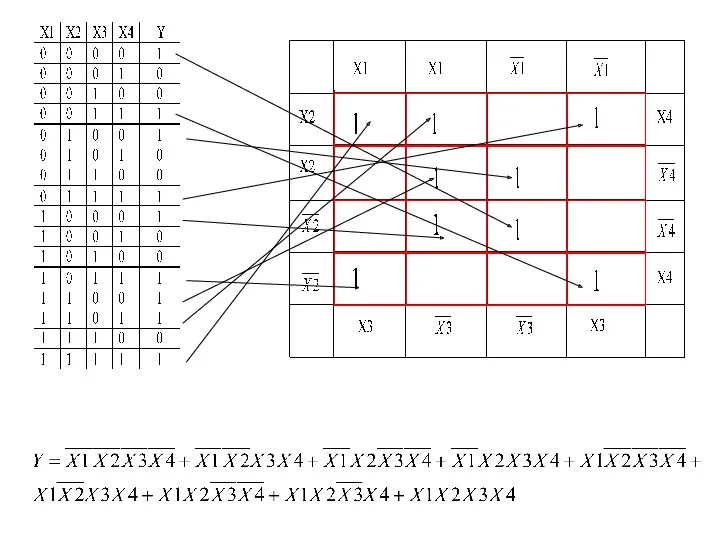
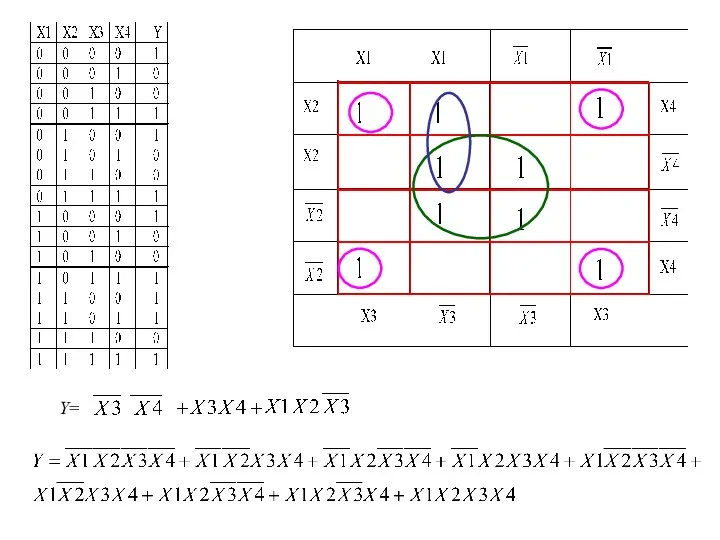
- 19. Для 4-х переменных
- 20. Соседними называют клетки - справа, слева, сверху, снизу. Если минтермы расположены в соседних клетках, то говорят,
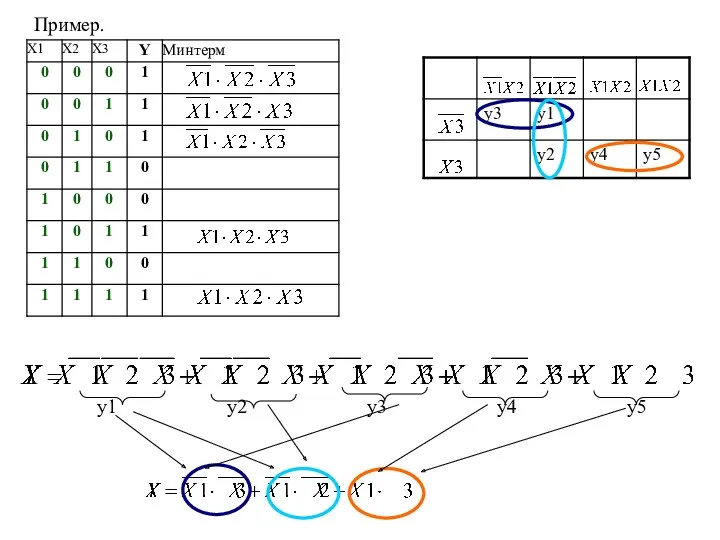
- 21. Пример. y1 y2 y3 y4 y5
- 22. Такой же результат получается, если воспользоваться логическими преобразованиями с помощью аксиом и законов АЛ. =1 =1
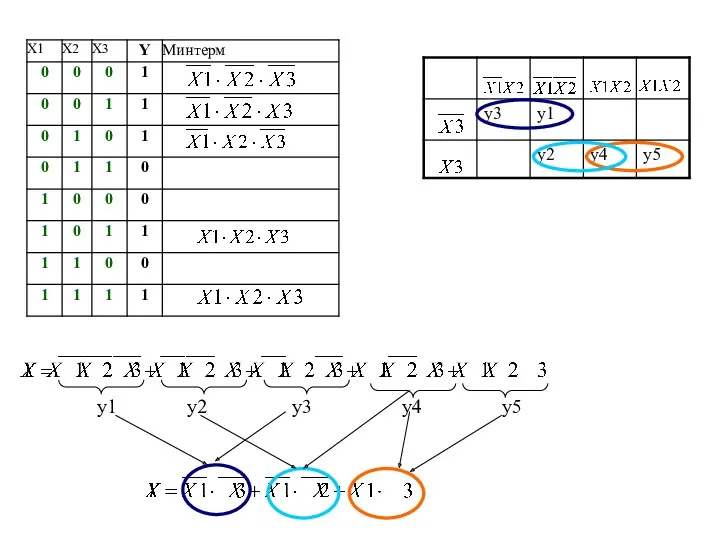
- 23. y1 y2 y3 y4 y5
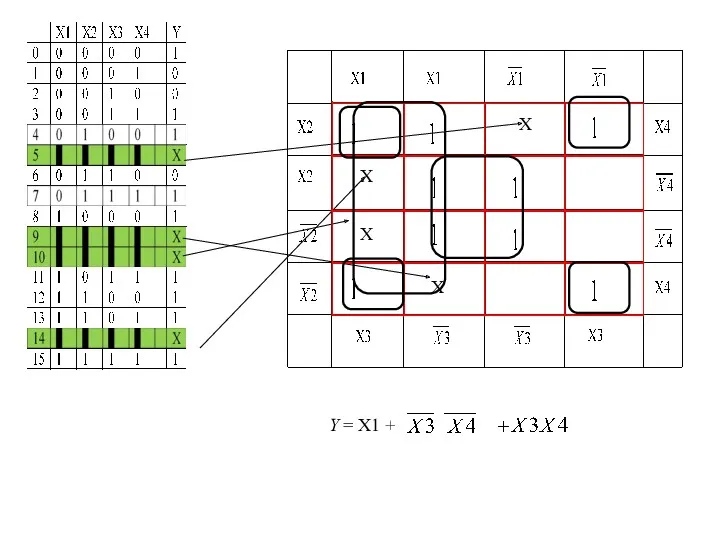
- 25. Y=
- 26. X X X X Y = X1 +
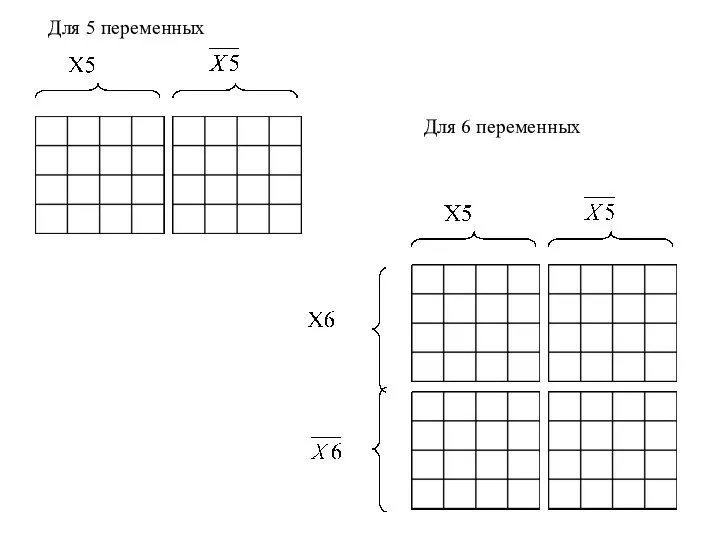
- 27. Для 5 переменных Для 6 переменных
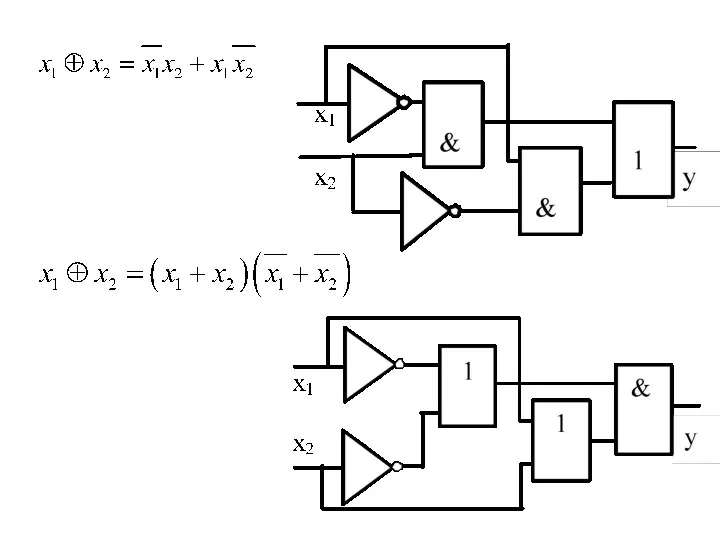
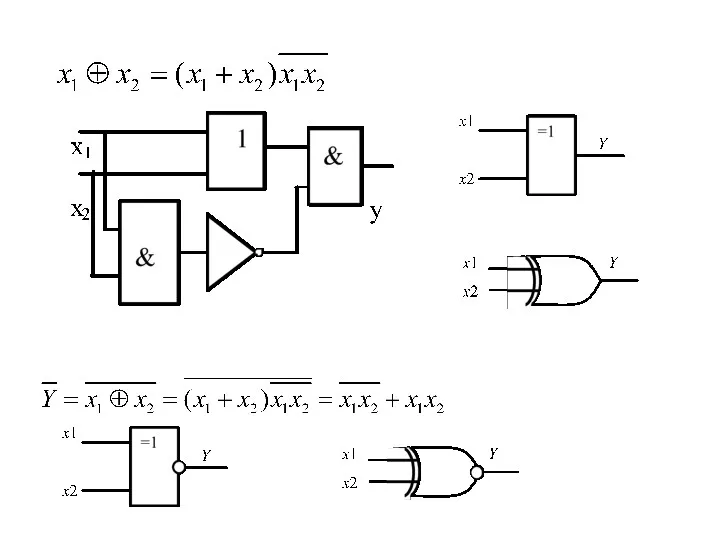
- 28. Пример. Рассмотрим ЛФ «исключающая ИЛИ» (операция сложения по модулю два, неравнозначность). ЛФ (переключательную) можно составить из
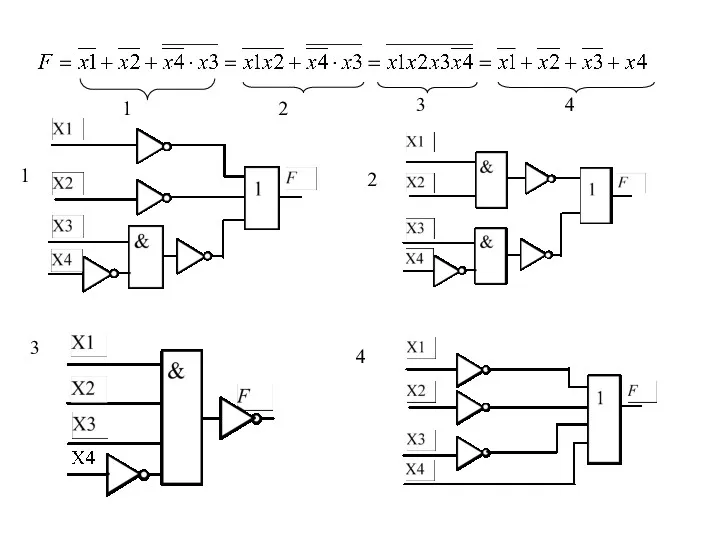
- 31. 1 2 3 4 1 2 4 3
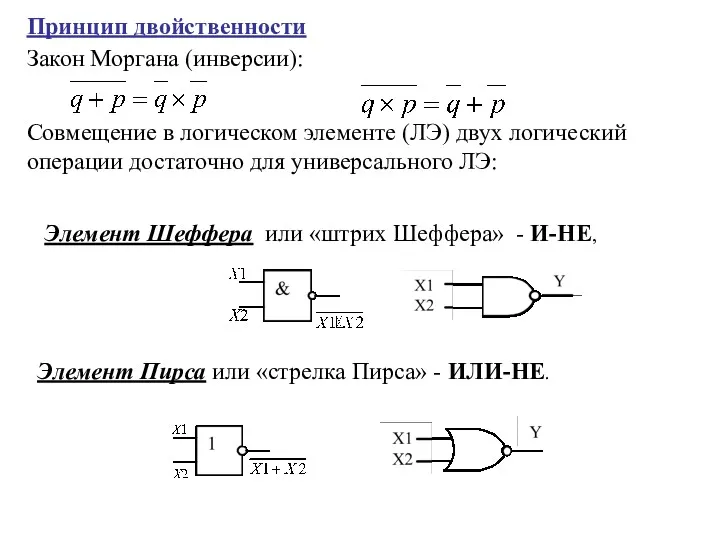
- 32. Принцип двойственности Элемент Шеффера или «штрих Шеффера» - И-НЕ, Элемент Пирса или «стрелка Пирса» - ИЛИ-НЕ.
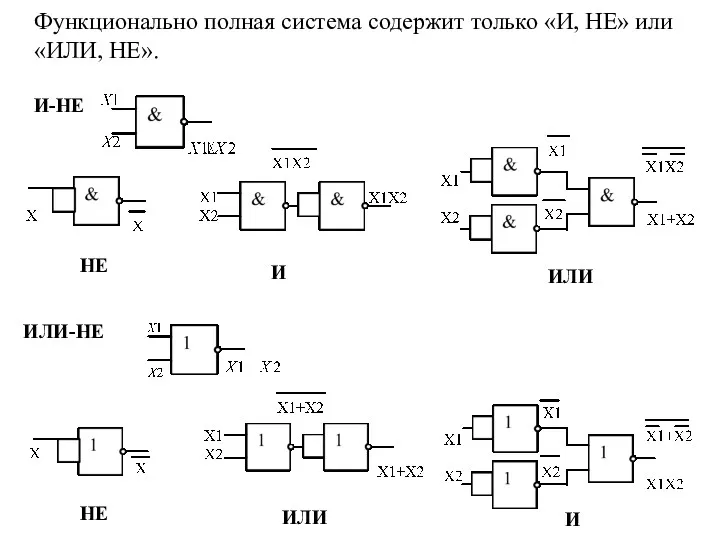
- 33. И-НЕ НЕ И ИЛИ ИЛИ-НЕ И НЕ ИЛИ Функционально полная система содержит только «И, НЕ» или
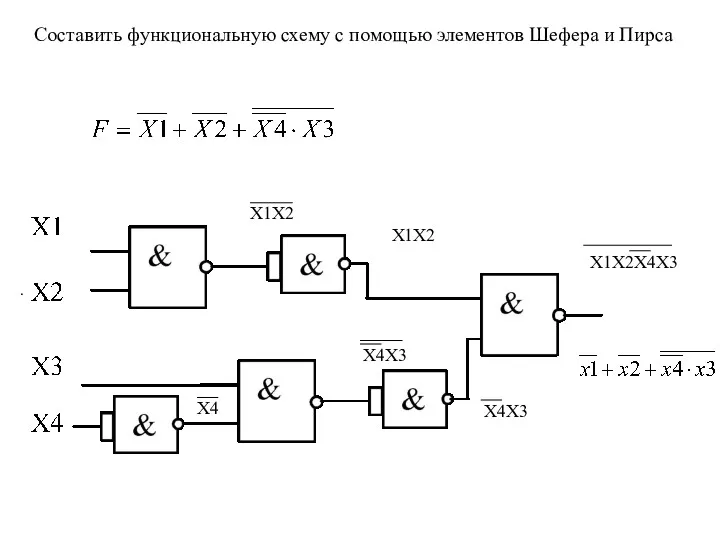
- 34. Составить функциональную схему с помощью элементов Шефера и Пирса . X1X2
- 36. Скачать презентацию








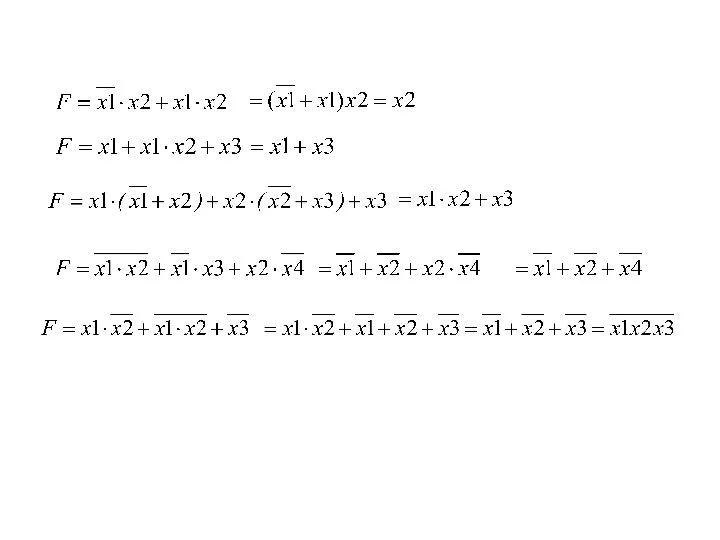





 Столбчатые диаграммы и графики
Столбчатые диаграммы и графики Презентация Письменные вычисления
Презентация Письменные вычисления Способы представления статистических данных
Способы представления статистических данных Методы оптимизации
Методы оптимизации Тест по теме: Линейные операции над векторами
Тест по теме: Линейные операции над векторами Своя игра по математике, 6 класс
Своя игра по математике, 6 класс Презентация к уроку математики в 4 классе.Деление на двузначные и трёхзначные числа.
Презентация к уроку математики в 4 классе.Деление на двузначные и трёхзначные числа. Своя игра по математике
Своя игра по математике Деление с остатком (5 класс)
Деление с остатком (5 класс) Что есть угол? Математика. Лекция №6
Что есть угол? Математика. Лекция №6 Решение задач части В (В1, В4)
Решение задач части В (В1, В4) Магические квадраты
Магические квадраты Сравнение, сложение, вычитание дробей с разными знаменателями. 6 класс
Сравнение, сложение, вычитание дробей с разными знаменателями. 6 класс Перестановка слагаемых. Применение переместительного свойства
Перестановка слагаемых. Применение переместительного свойства Нахождение числа по заданному значению его дроби
Нахождение числа по заданному значению его дроби Объемы наклонной призмы, пирамиды, конуса
Объемы наклонной призмы, пирамиды, конуса Задача о максимальном потоке и алгоритм Форда–Фалкерсона
Задача о максимальном потоке и алгоритм Форда–Фалкерсона Обратные задачи
Обратные задачи Пример решения транспортной задачи (закрытая модель). Исследование операций
Пример решения транспортной задачи (закрытая модель). Исследование операций Подобные треугольники
Подобные треугольники Квадратичная функция у = ах2 + bx + c
Квадратичная функция у = ах2 + bx + c Логарифмическая функция и ее свойства
Логарифмическая функция и ее свойства Теорема Пифагора (вне школьной программы)
Теорема Пифагора (вне школьной программы) Числа от 1 до 10
Числа от 1 до 10 Использование информационных технологий на уроках математики
Использование информационных технологий на уроках математики Координаты на прямой
Координаты на прямой Теорема о медиане треугольника
Теорема о медиане треугольника Уравнение данной линии
Уравнение данной линии