Содержание
- 2. 4096tb@gmail.com Тема письма: БГУИР. … . Ковалевский Вячеслав Викторович
- 3. Лекция 1. Представление информации. Системы счисления. Формат с фиксированной запятой План лекции: История развития вычислительной техники.
- 4. Лекция 2. Формат с плавающей запятой. Стандарт IEEE 754. Погрешности. Обратная польская запись План лекции: Формат
- 5. Лекция 3. Логические основы ЭВМ. Минимизация. План лекции: Понятия алгебры логики. Аксиомы и законы алгебры логики.
- 6. Булева алгебра Джордж Буль (George Boole) 02.11.1815 — 08.12.1864 Известный английский математик и логик. Автор «логических
- 7. Алгебра логики (Булева алгебра) Алгебра логики рассматривает высказывания и их взаимосвязь только с точки зрения их
- 8. Логические функции Независимые высказывания называют аргументами. Высказывания, истинность либо ложность которых зависит от истинности либо ложности
- 9. Для упрощения записей значения «Ложь» и «Истина» обозначают нулем и единицей (0 и 1). Логические переменные
- 10. x = 0 x1 = Ложь x2 = 1 y = False Alpha = Истинна Omega
- 11. Аксиомы конъюнкции 0*0=0 0*1=0 1*1=1 Аксиомы дизъюнкции 0+0=0 0+1=1 1+1=1 Аксиомы отрицания If x=0, then ̅x̅=1
- 12. Теоремы Булевой алгебры Теоремы исключения констант x*0=0 x*1=x x+1=1 x+0=x Теоремы идемпотентности (тавтологии, повторения) x*x=x x+x=x
- 13. Законы Булевой алгебры Ассоциативный (сочетательный) закон x1*(x2*x3) = (x1*x2)*x3 x1+(x2+x3) = (x1+x2)+x3 Коммутативный (переместительный) закон x1*x2
- 14. Правило де Мóргана или
- 15. Правило де Мóргана или Отрицание конъюнкции есть дизъюнкция отрицаний: Отрицание дизъюнкции есть конъюнкция отрицаний:
- 16. Формы представления логических функций Таблица истинности Аналитическое выражение Логическая схема
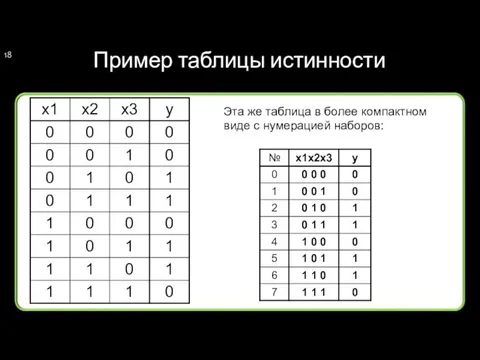
- 17. Таблица истинности Таблица истинности описывает значения логической функции на всех наборах ее аргументов. Для функции, зависящей
- 18. Пример таблицы истинности Эта же таблица в более компактном виде с нумерацией наборов:
- 19. Аналитическое выражение При аналитической записи функция представляется либо в виде логической суммы элементарных логических произведений (дизъюнкции
- 20. Аналитическое представление логических функций ДНФ: КНФ:
- 21. СДНФ и СКНФ СДНФ – совершенная дизъюнктивная нормальная форма представления логической функции. СДНФ – это дизъюнкция
- 22. СДНФ (совершенная дизъюнктивная нормальная форма) СДНФ логической функции – это дизъюнкция конституент единицы (минтермов), соответствующих наборам
- 23. СКНФ (совершенная конъюнктивная нормальная форма) СКНФ логической функции – это конъюнкция конституент нуля (макстермов), соответствующих входным
- 24. СДНФ и СКНФ Совершенная – во всех членах присутствуют все аргументы. Нормальная – «без скобок». Дизъюнктивная
- 25. СДНФ и СКНФ Совершенная дизъюнктивная нормальная форма (СДНФ) Функция представляется суммой групп. Каждая группа состоит из
- 26. Примеры СДНФ и СКНФ СДНФ – это дизъюнкция конъюнкций. СКНФ – это конъюнкция дизъюнкций.
- 27. СДНФ из таблицы истинности Чтобы записать СДНФ функции, нужно записать все конституенты единицы (т.е. конъюнкции), причем
- 28. СДНФ из таблицы истинности СДНФ: Таблица истинности:
- 29. Функционально полная система логических функций (ФПС ЛФ) (Булев или логический базис) это такой набор логических функций,
- 30. Конъюнкция (И) Конъюнкция истинна тогда и только тогда, когда истинны все ее аргументы
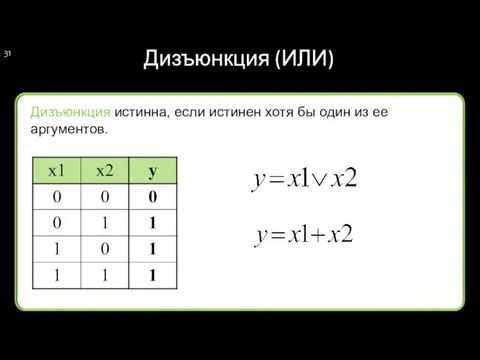
- 31. Дизъюнкция (ИЛИ) Дизъюнкция истинна, если истинен хотя бы один из ее аргументов.
- 32. Отрицание (Инверсия) Инверсия принимает значение, противоположное значению ее аргумента
- 33. И-НЕ (Not AND, NAND)
- 34. ИЛИ-НЕ (Not OR, NOR)
- 35. Исключающее ИЛИ (XOR)
- 36. Логические элементы Это устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов как правило в
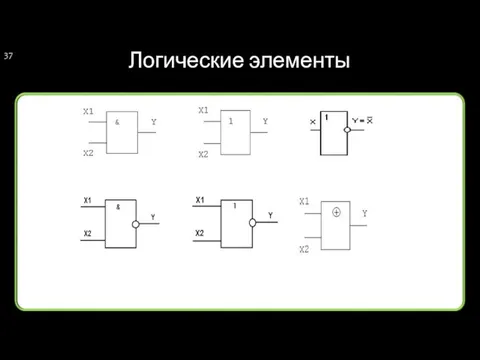
- 37. Логические элементы
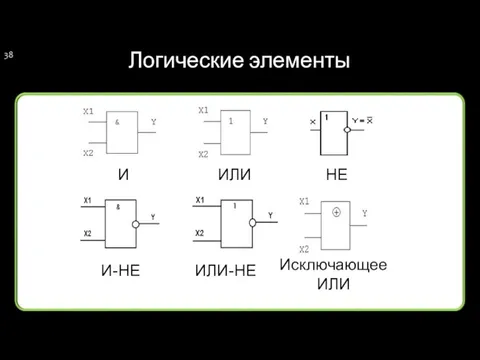
- 38. Логические элементы ИЛИ И НЕ И-НЕ ИЛИ-НЕ Исключающее ИЛИ
- 39. Элементы И, ИЛИ, НЕ в альтернативном обозначении
- 40. Логические (комбинационные) схемы Логическая схема (ЛС), или схема «без памяти», состоит из логических элементов (ЛЭ), соединенных
- 41. Пример логической схемы
- 42. Минимизация логических функций Преобразование СДНФ или СКНФ логической функции к минимальному виду аналитической записи называется процессом
- 43. Аксиомы алгебры логики
- 44. Склеивание Таким образом, Такое преобразование называется склеиванием. Конъюнкции и называются соседними. Они «склеиваются по »
- 45. Примеры склеивания
- 46. Алгоритмические методы минимизации Позволяют проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся:
- 47. Карты Карно Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом
- 48. Пример таблицы истинности, СДНФ, СКНФ СДНФ: СКНФ: Таблица истинности:
- 49. Карты Карно (диаграммы Вейча) Перепишем таблицу истинности функции следующим образом: Код Грея
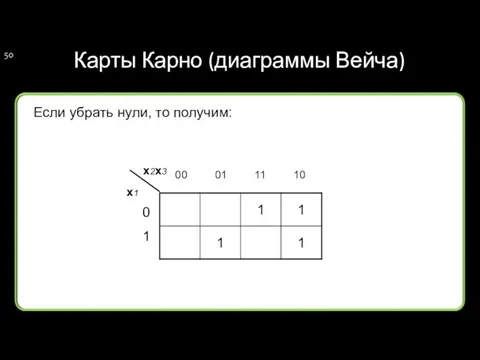
- 50. Карты Карно (диаграммы Вейча) Если убрать нули, то получим:
- 51. Карты Карно (диаграммы Вейча) Единицы, расположенные в соседних клетках, соответствуют соседним конъюнкциям.
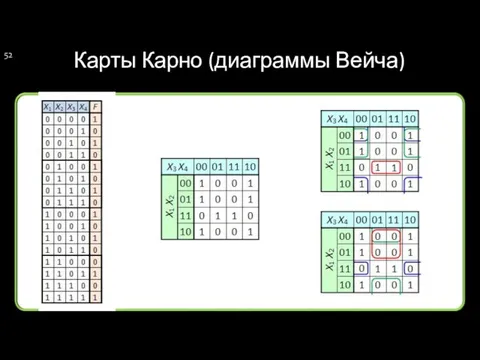
- 52. Карты Карно (диаграммы Вейча)
- 53. Карты Карно (диаграммы Вейча) Выражение в формате ДНФ: Выражение в формате КНФ:
- 54. Пример минимизации логической функции У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдёт гулять
- 55. Пример минимизации логической функции Составим таблицу истинности: Применяя Код Грея подготовим Карту Карно: Заполним Карту Карно
- 56. Пример минимизации логической функции Минимизируем в соответствии с правилами, получим минимальную ДНФ:
- 57. Пример минимизации логической функции По полученной минимальной ДНФ можно построить логическую схему:
- 58. Пример минимизации логической функции Минимизируем в соответствии с правилами, получим минимальную КНФ:
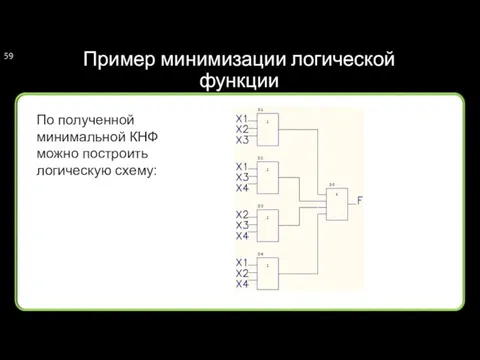
- 59. Пример минимизации логической функции По полученной минимальной КНФ можно построить логическую схему:
- 61. Скачать презентацию



















































 Игровые технологии на уроках математики в 5-6 классах
Игровые технологии на уроках математики в 5-6 классах Игра Крестики-нолики. Тема: Треугольники
Игра Крестики-нолики. Тема: Треугольники Арифметик һәм геометрик прогрессияләрнең беренче n буыны суммасы темасын гомумиләштерү
Арифметик һәм геометрик прогрессияләрнең беренче n буыны суммасы темасын гомумиләштерү Презентация Периметр Диск
Презентация Периметр Диск Первый признак равенства треугольников
Первый признак равенства треугольников Geometrical shapes
Geometrical shapes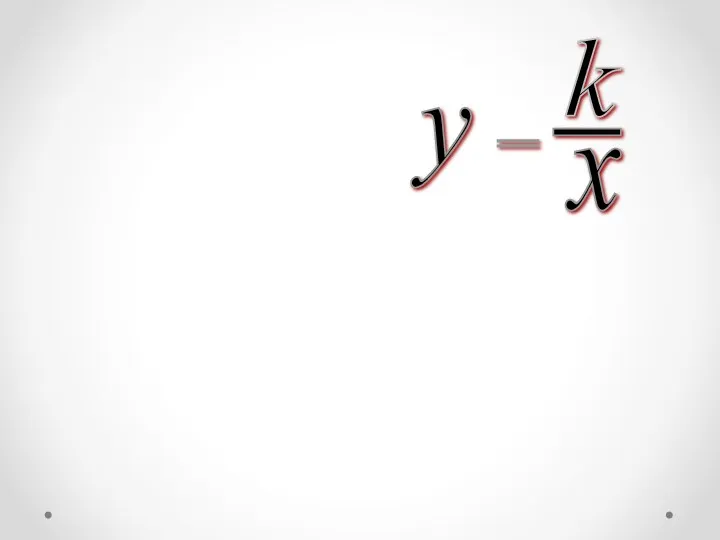 Функция обратной пропорциональности и её график
Функция обратной пропорциональности и её график Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Как найти неизвестное вычитаемое
Как найти неизвестное вычитаемое Виды треугольников 4 класс
Виды треугольников 4 класс Линейные уравнения с параметрами (7 класс)
Линейные уравнения с параметрами (7 класс) Математика в моей будущей профессии
Математика в моей будущей профессии Предел числовой последовательности
Предел числовой последовательности Интегрированный урок математики и английского языка Повторение изученного в в 1 классе
Интегрированный урок математики и английского языка Повторение изученного в в 1 классе Взаимно обратные числа
Взаимно обратные числа Применение производной для исследования функций на монотонность
Применение производной для исследования функций на монотонность Умножение и деление
Умножение и деление Логіка предикатів. (Лекция 3)
Логіка предикатів. (Лекция 3) Умножение дроби на натуральное число. Урок математики. 6 класс
Умножение дроби на натуральное число. Урок математики. 6 класс Решение показательных уравнений и неравенств. 12 класс
Решение показательных уравнений и неравенств. 12 класс Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Элементы математической статистики
Элементы математической статистики Арифметический корень n-ой степени
Арифметический корень n-ой степени Сикһеҙ геометрик прогрессия
Сикһеҙ геометрик прогрессия Основное свойство дроби
Основное свойство дроби Умножение смешанных дробей
Умножение смешанных дробей Метрология. Калибровка средств измерений. (Лекция 4)
Метрология. Калибровка средств измерений. (Лекция 4) Transformations of block diagram
Transformations of block diagram