Содержание
- 2. Логическая символика
- 3. 1 Понятие множества Множество (set) – некоторая, вполне определенная совокупность объектов произвольной природы, каждый их которых
- 4. Примеры множеств
- 5. Объекты, которые образуют множество, называются его элементами. Бесконечное множество содержит бесконечное число элементов. Конечное множество состоит
- 6. Обозначения В дальнейшем множества будем обозначать прописными латинскими буквами, элементы – строчными латинскими. a ∈ A
- 7. Множество, не содержащее ни одного элемента, называется пустым и обозначается ∅. Пример. Множество оценок в зачетке
- 8. Множество B называется подмножеством множества A, если каждый элемент множества В является элементом множества А. Рис.
- 9. Два множества А и В называются равными, если они состоят из одних и тех же элементов.
- 10. Универсальное множество U есть совокупность всех рассматриваемых в задаче множеств. Пример. Имеются два множества: A =
- 11. Числовые множества N ={1, 2, 3…} – множество натуральных чисел; Z ={0, ±1, ±2, ±3,… }
- 12. 2 Операции над множествами 2-1 Объединение (сумма) 2-2 Пересечение (произведение) 2-3 Разность (вычитание) 2-4 Симметрическая разность
- 13. Объединением (суммой) двух множеств А и В называется множество С, состоящее из всех элементов, принадлежащих хотя
- 14. Пересечением (произведением) двух множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих
- 15. Разностью двух множеств А и В называется множество F, состоящее из всех элементов принадлежащих множеству А,
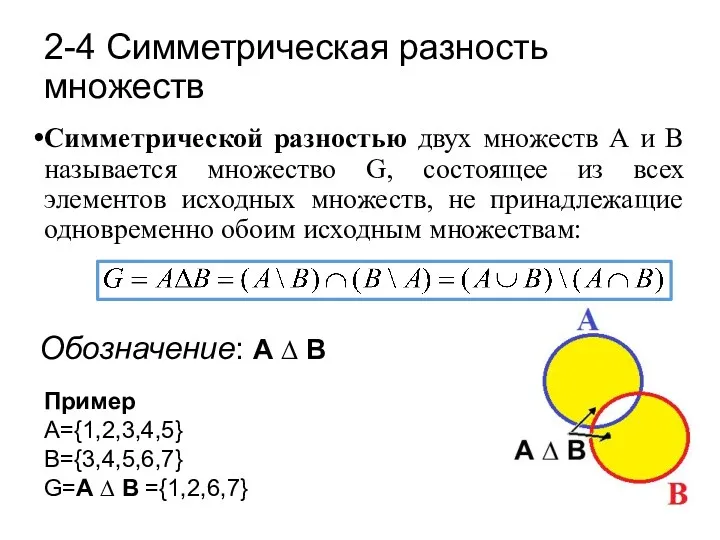
- 16. Симметрической разностью двух множеств А и В называется множество G, состоящее из всех элементов исходных множеств,
- 17. Дополнением к множеству A называется множество элементов универсального множества, не принадлежащих A: Ᾱ = U –
- 18. Для введенных операций присущи следующие свойства: 2-6 Свойства операций над множествами
- 19. 3 Числовые промежутки и ограниченные множества
- 20. Числовые промежутки
- 21. Окрестность точки (neighborhood of point) Абсолютная величина разности двух чисел |x – a| означает расстояние между
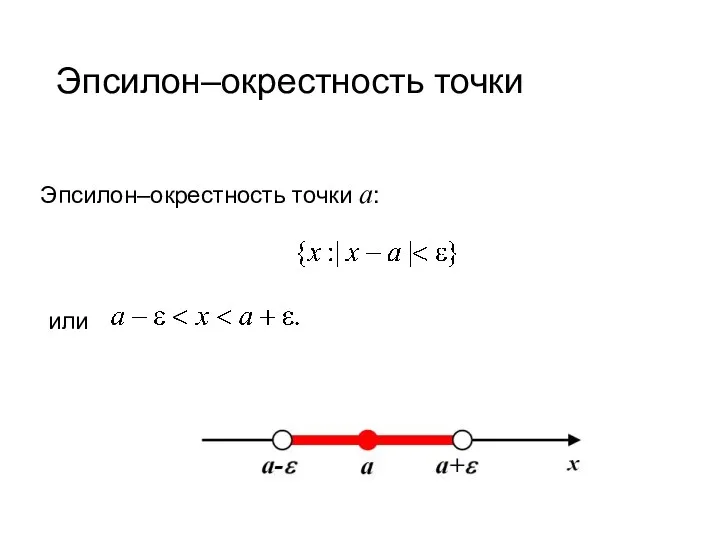
- 22. Эпсилон–окрестность точки Эпсилон–окрестность точки a: или .
- 23. Ограниченные множества
- 24. Если множество Х ограничено сверху, то говорят, что множество имеет верхнюю границу Наименьшая из верхних границ
- 25. Задача. Найти точную верхнюю и точную нижнюю грани множества [0, 1). Решение. 1. Это множество не
- 26. С другой стороны, наименьший элемент для рассматриваемого множества существует и равен 0. Множество нижних граней –
- 27. 4 Числовые последовательности 1 Определение последовательности 2 Предел последовательности 3 Теоремы о пределах 4 Бесконечно большие
- 28. 4-1 Определение последовательности Если каждому натуральному числу n по определенному закону поставлено в соответствие некоторое число
- 29. Примеры последовательностей
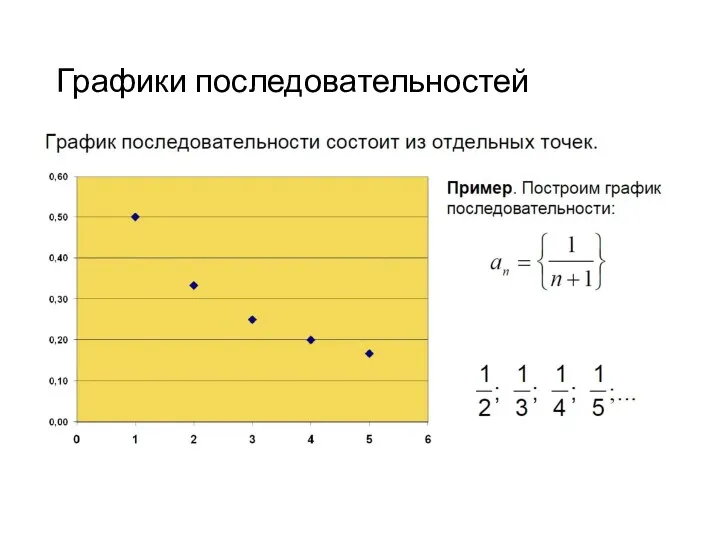
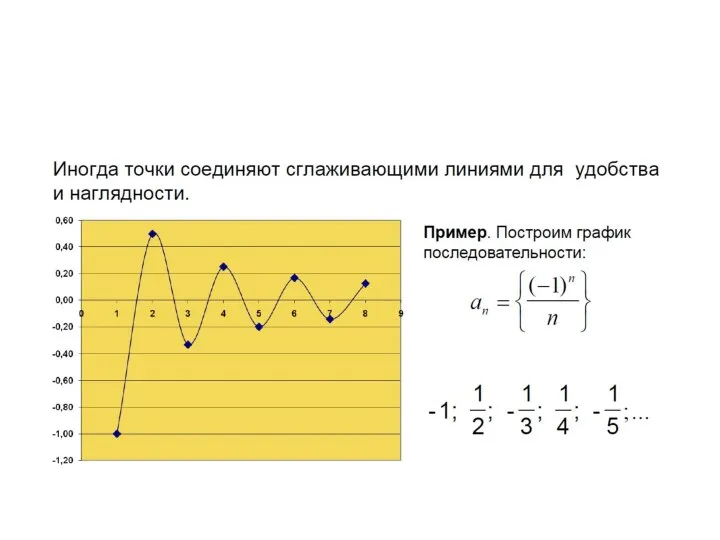
- 30. Графики последовательностей
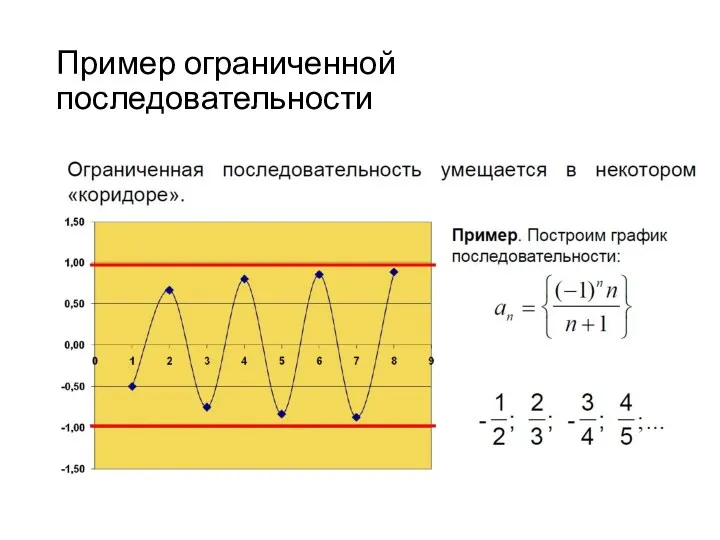
- 32. Ограниченная последовательность
- 33. ПРИМЕРЫ
- 34. Пример ограниченной последовательности
- 36. 4-2 Предел последовательности Понятие последовательности Определение предела последовательности Геометрический смысл
- 37. Предел последовательности
- 38. Предел числовой последовательности
- 39. Определение предела в кванторах
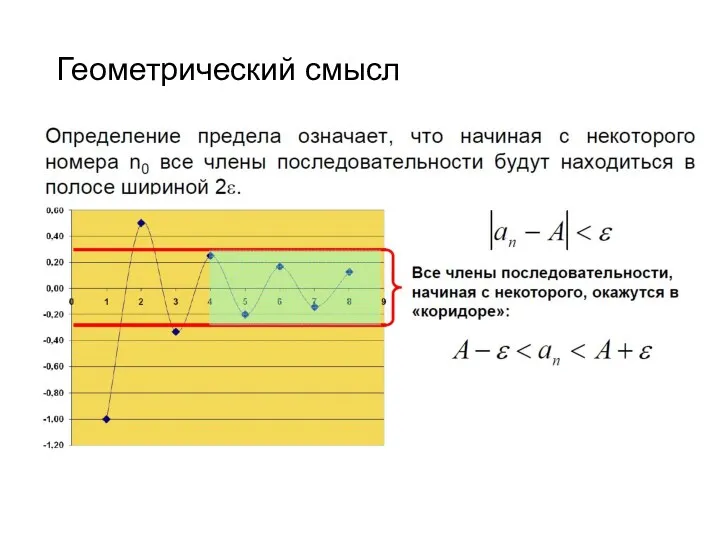
- 41. Геометрический смысл
- 42. пример 1
- 43. решение примера 1
- 44. решение примера 1(продолжение)
- 45. пример 2
- 48. пример 3
- 49. Кому нужен такой «формализм»?
- 50. Ответ
- 51. 4-3 Основные теоремы о пределах Единственность предела Предел суммы, произведения, частного Признаки существования предела
- 52. Единственность предела
- 53. Предел суммы
- 54. Пределы произведения и частного
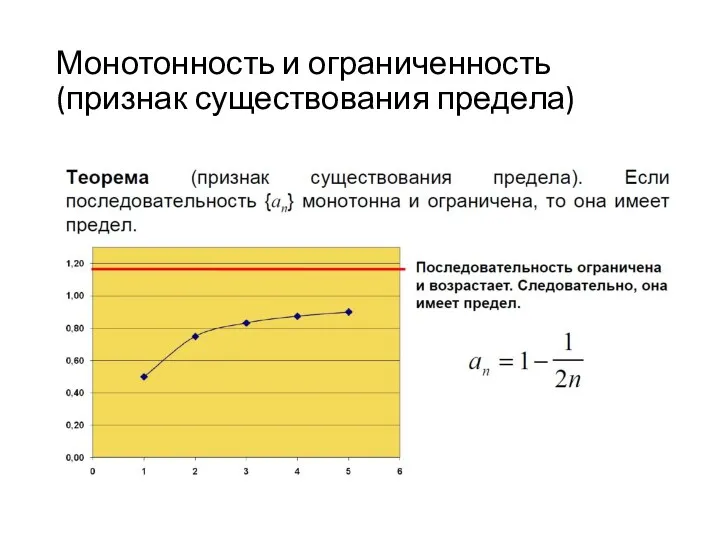
- 55. Монотонность и ограниченность (признак существования предела)
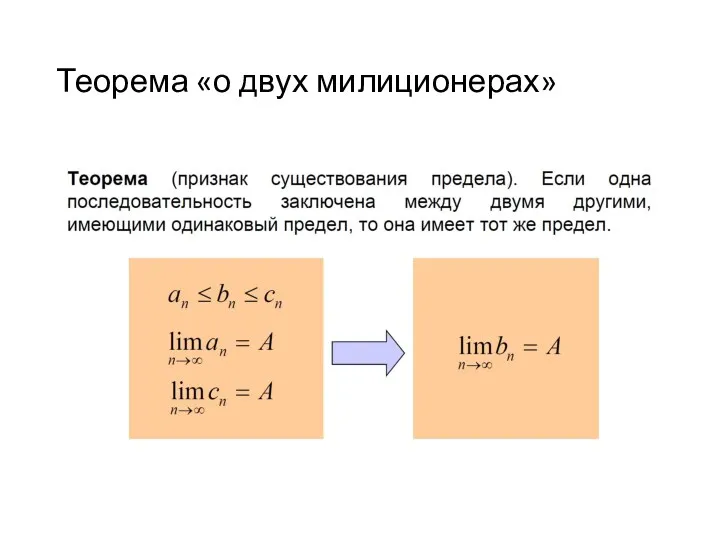
- 56. Теорема «о двух милиционерах»
- 57. 4-4 Бесконечно большие и бесконечно малые последовательности
- 60. Свойства бесконечно малых последовательностей
- 62. Примеры бесконечно малых последовательностей
- 63. 4-5 Вычисление пределов
- 65. Скачать презентацию





















































 Интегрированный урок математики и окружающего мира во 2 классе.
Интегрированный урок математики и окружающего мира во 2 классе. Способы решения задач на смеси и сплавы. Арифметический. Применение уравнения. Применение систем уравнений
Способы решения задач на смеси и сплавы. Арифметический. Применение уравнения. Применение систем уравнений Применение свойств квадратного корня
Применение свойств квадратного корня Нахождение части от целого и целого по его части
Нахождение части от целого и целого по его части Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Логика высказываний
Логика высказываний Игра- путешествие по математике ( 1 класс)
Игра- путешествие по математике ( 1 класс) Решение задач профильного ЕГЭ по теме Теория вероятности
Решение задач профильного ЕГЭ по теме Теория вероятности Вписанные и описанные окружности. Задания для устного счета. Упражнение 14. 8 класс
Вписанные и описанные окружности. Задания для устного счета. Упражнение 14. 8 класс волшебная полянка 1
волшебная полянка 1 Периметр прямоугольника
Периметр прямоугольника математика
математика Завдання з геометрії
Завдання з геометрії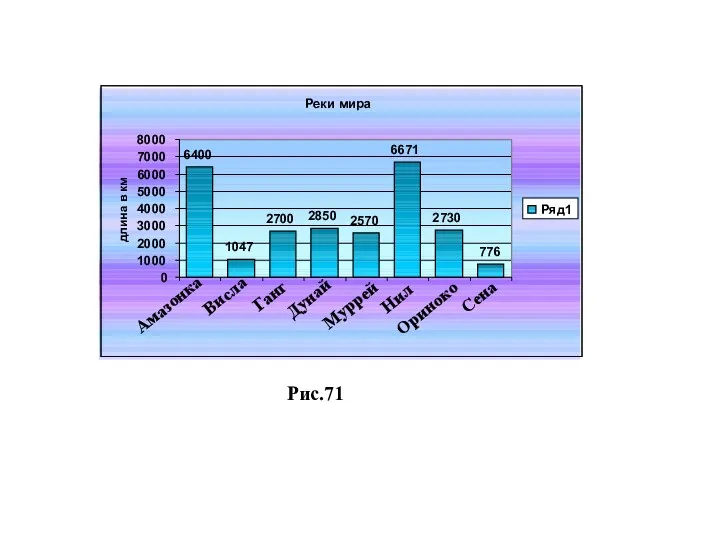 Чтение диаграмм, 6 класс
Чтение диаграмм, 6 класс Учимся решать логические задачи ( 1-2 класс )
Учимся решать логические задачи ( 1-2 класс ) Взаимное расположение прямых в пространстве. Задания для устного счета. Упражнение 3
Взаимное расположение прямых в пространстве. Задания для устного счета. Упражнение 3 Решение задач и выражений
Решение задач и выражений Разработка урока математики во 2 классе с использованием ИКТ
Разработка урока математики во 2 классе с использованием ИКТ Правильный многоугольник
Правильный многоугольник Определенный интеграл. Формула интегрирования по частям (пример 1)
Определенный интеграл. Формула интегрирования по частям (пример 1) Умножение двузначного числа на однозначное. Урок математики 3 класс
Умножение двузначного числа на однозначное. Урок математики 3 класс Предел Бесконечно маленькая величина
Предел Бесконечно маленькая величина Статистическая сводка и группировка
Статистическая сводка и группировка Математический кроссворд
Математический кроссворд Среднее арифметическое
Среднее арифметическое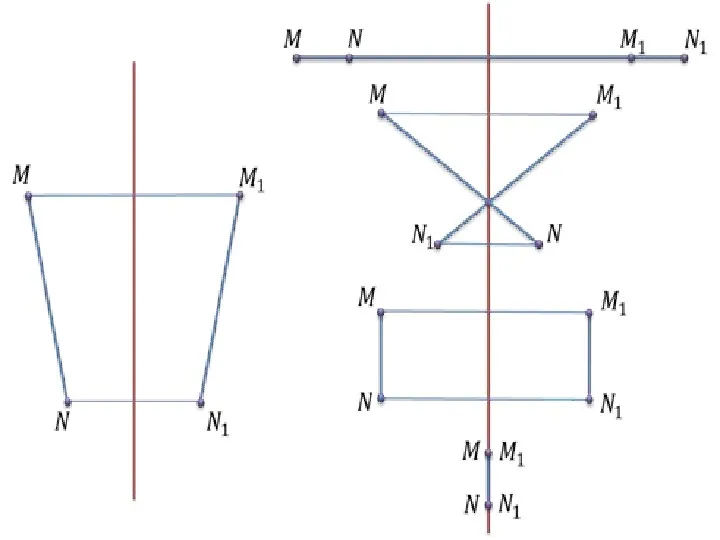 Симметричные фигуры
Симметричные фигуры Разложение многочлена на множители
Разложение многочлена на множители Применение производной и первообразной показательной и логарифмической функции
Применение производной и первообразной показательной и логарифмической функции