Содержание
- 2. Индуктивное умозаключение — метод рассуждения от частного к общему. Метод доказательства, при котором проверяется утверждение для
- 3. Например, утверждение: «Каждое двузначное чётное число является суммой двух простых чисел» – следует из серии равенств,
- 4. Способ доказательства методом математической индукции заключается в следующем: база индукции: доказывают или непосредственно проверяют справедливость утверждения
- 5. Доказать , что при любом натуральном n число 32n+1+2n+2 делится на 7. Обозначим А(n)=32n+1+2n+2. База индукции.
- 6. На плоскости дано n окружностей. Доказать, что при любом расположении этих окружностей образуемую ими карту можно
- 7. Предположим, что утверждение справедливо для любой карты, образованной n окружностями, и пусть на плоскости задано n+1
- 8. Восстановим затем отброшенную окружность и по одну сторону от нее, например внутри, изменим цвет каждой области
- 9. В плоскости проведено n прямых, из которых никакие две не параллельны и никакие три не проходят
- 11. Сделав предположение индукции рассмотрим k+1 прямых, удовлетворяющих условию задачи. Выделим из них произвольным образом k прямых.
- 12. В любой момент времени число людей на земле , сделавших нечётное число рукопожатий , чётно.
- 13. Назовём людей, сделавших нечётное число рукопожатий «плохими», а остальных «хорошими». После рукопожатия с номером 1 стало
- 14. Пусть происходит рукопожатие номер к+1. При этом может быть 3 случая: Пожимают руки двое «хороших», двое
- 16. Скачать презентацию








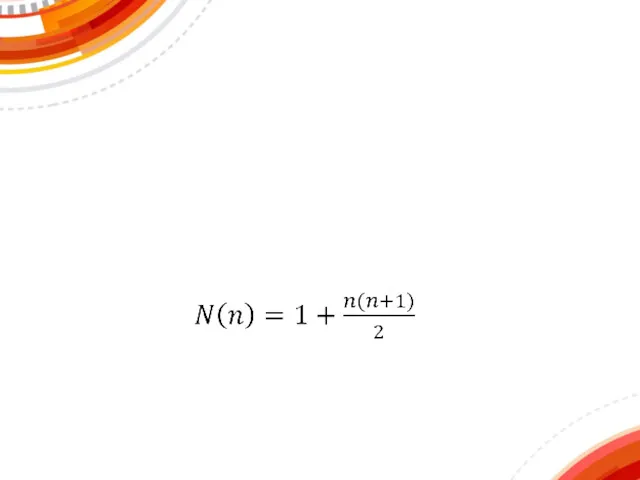




 Логарифмы и их применение
Логарифмы и их применение Комплексные числа
Комплексные числа Урок-презентация по математике в 4 классе
Урок-презентация по математике в 4 классе Приемы устных вычислений вида 450+30, 620-200
Приемы устных вычислений вида 450+30, 620-200 Формирование регулятивных универсальных учебных действий на уроках математики в начальной школе
Формирование регулятивных универсальных учебных действий на уроках математики в начальной школе Наибольший общий делитель. Взаимно простые числа
Наибольший общий делитель. Взаимно простые числа Внеклассное мероприятие по математике Своя игра (для учащихся 5-х классов)
Внеклассное мероприятие по математике Своя игра (для учащихся 5-х классов) Поговорим о многогранниках
Поговорим о многогранниках Площадь треугольника. Теоремы, следствия и задачи
Площадь треугольника. Теоремы, следствия и задачи Теоретические основы математической логики
Теоретические основы математической логики Занимательная математика. Игра
Занимательная математика. Игра Екі түзудің өзара орналасуы
Екі түзудің өзара орналасуы Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел Презентация к уроку в 1-м классе Сложение и вычитание отрезков
Презентация к уроку в 1-м классе Сложение и вычитание отрезков Сложение и вычитание в пределах 100. Урок закрепления
Сложение и вычитание в пределах 100. Урок закрепления Обыкновенные дроби
Обыкновенные дроби Действия с дробями
Действия с дробями Медиа-сопровождение к уроку математики Число 9. Цифра 9
Медиа-сопровождение к уроку математики Число 9. Цифра 9 Синус, косинус и тангенс углов от 0⁰ до 180 ⁰
Синус, косинус и тангенс углов от 0⁰ до 180 ⁰ Тест по геометрии
Тест по геометрии Незнайкины задачки. Математика. 1 класс
Незнайкины задачки. Математика. 1 класс Прямая и обратная пропорциональность
Прямая и обратная пропорциональность Түзу мен жазықтық арасындағы бұрыш. Екі жазықтық арасындағы бұрыш. Екі жақты бұрыш
Түзу мен жазықтық арасындағы бұрыш. Екі жазықтық арасындағы бұрыш. Екі жақты бұрыш Софья Васильевна Ковалевская (1850-1891)
Софья Васильевна Ковалевская (1850-1891) Тригонометрия. Применение тригонометрии
Тригонометрия. Применение тригонометрии Площадь треугольника
Площадь треугольника Перспективные масштабы геометрических тел
Перспективные масштабы геометрических тел Роль исследовательской деятельности в формировании познавательного интереса на уроках математики
Роль исследовательской деятельности в формировании познавательного интереса на уроках математики