Метод замены множителей. Показательная и логарифмическая функции и вызываемые ими замены презентация
Содержание
- 2. Замечание. Преобразованное таким образом неравенство равносильно исходному в области его определения. Предупреждение. Указанная замена возможна только
- 3. Монотонность – ключ к замене Утверждение 1. Функция строго возрастает тогда и только тогда, когда для
- 4. Функция и вызываемые ею замены Поскольку функция при является строго возрастающей на множестве неотрицательных чисел (а
- 5. Пример 1. Решить неравенство Решение (подробное). Исходное уравнение имеет вид Все множители u1, u2, v1 и
- 6. где знакопостоянные (D
- 7. Ответ:
- 8. Две любопытные замены: (9) (10) Замена (9) очень удобна там, где приходится отслеживать область допустимых значений.
- 9. Пример 2. Решить неравенство Решение. Ответ:
- 10. Пример 3. Решить неравенство Решение. Множители и уже нельзя рассматривать как разности неотрицательных величин, так как
- 11. так как при x>0 (x+1) и (3x+14) – положительные числа Ответ.
- 12. Показательная и логарифмическая функции и вызываемые ими замены Показательная функция строго убывает при и строго возрастает
- 13. Функция - строго возрастающая. Поэтому Если x1=a и x2=1, то получаем, что (12) Откуда соотношение (11)
- 14. Для логарифмической функции аналогично устанавливаем Отсюда следует, что То есть разность логарифмов по одному и тому
- 15. Замечание. Утверждения (14) и (13) равносильны, поскольку показательная и логарифмическая функции взаимно обратны. Эти утверждения также
- 16. 3) 4)
- 17. 6) 5)
- 18. Практика
- 19. Пример 1. Решение.
- 20. Пример 2. Решение.
- 21. Пример 3. Решение.
- 22. Пример 4. Решение.
- 23. Пример 5. Решение.
- 24. Пример 6. Решение.
- 25. Пример 7. Решение.
- 26. Пример 8. Решение.
- 28. Пример 9. Решение.
- 30. Пример 10. Решение.
- 32. Пример 11. Решение.
- 34. Пример 12. Решение.
- 36. Пример 13. Решение.
- 38. Пример 14. Решение.
- 39. Пример 15. Решение.
- 41. Пример 16. Решение.
- 44. Пример 17. Решение.
- 46. Пример 18. Решение.
- 48. Пример 19. Решение.
- 49. Пример 20. Решение.
- 51. Итоги
- 52. Основные замены: если f(t) – строго возрастающая функция; если f(t) – строго убывающая функция.
- 53. Наиболее часто встречающиеся замены (без учета ОДЗ):
- 58. Скачать презентацию














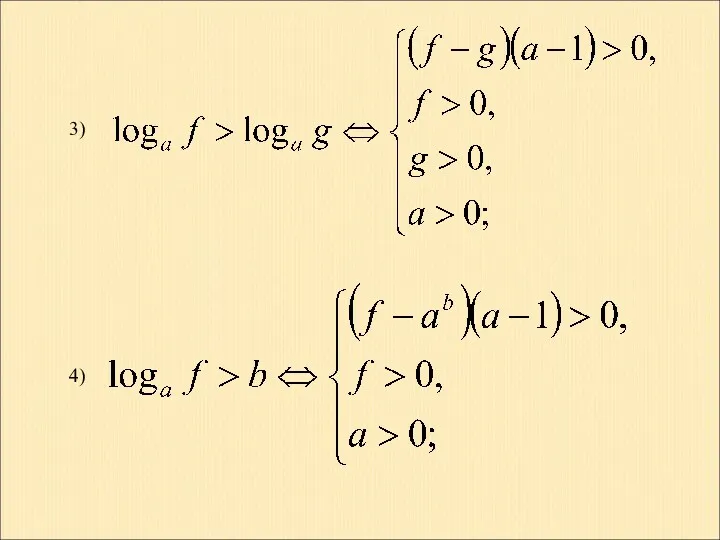
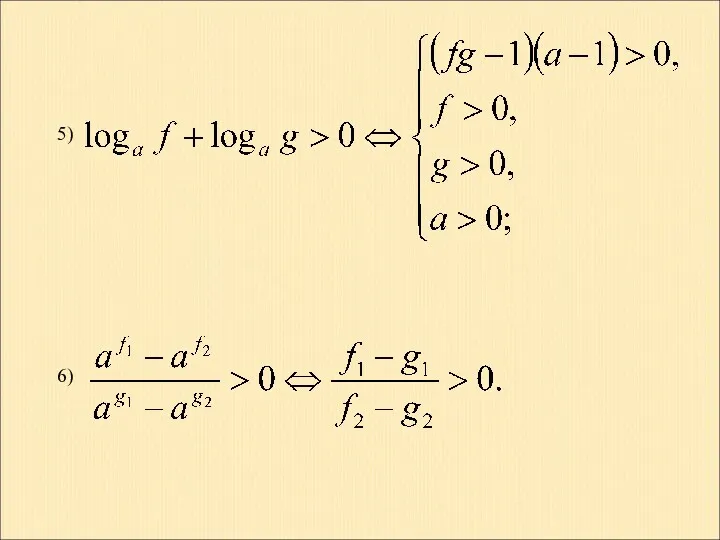

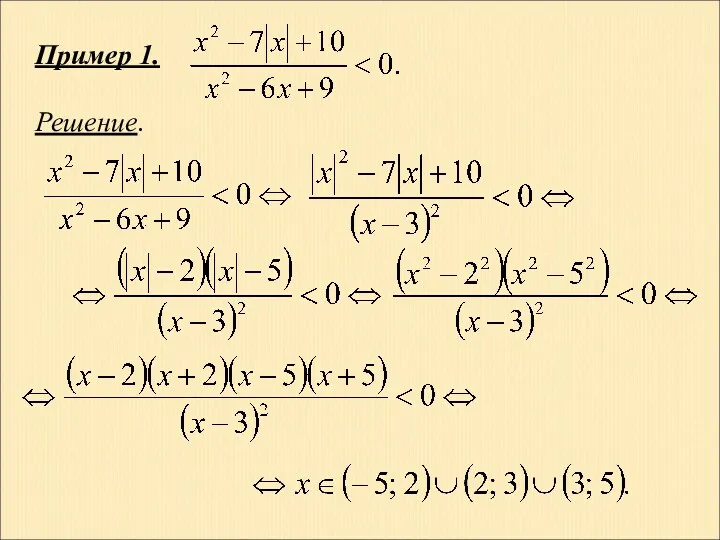




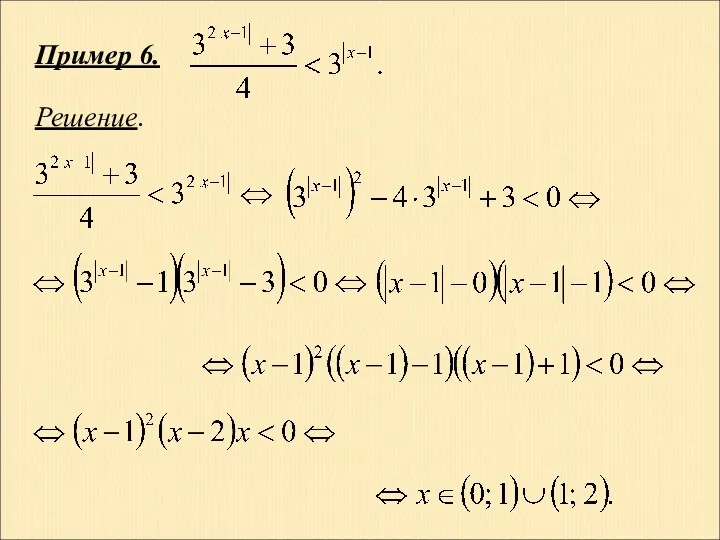


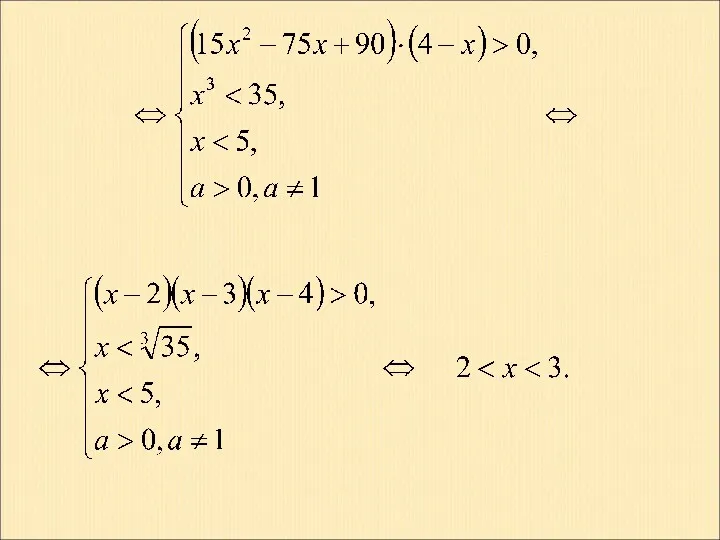










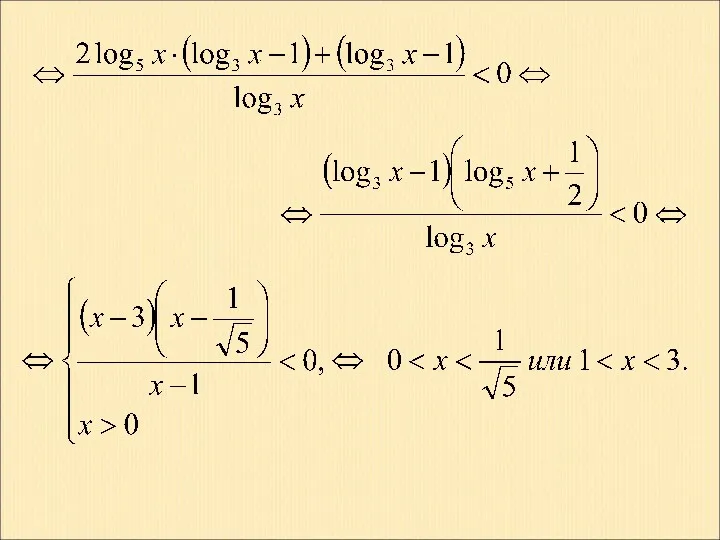

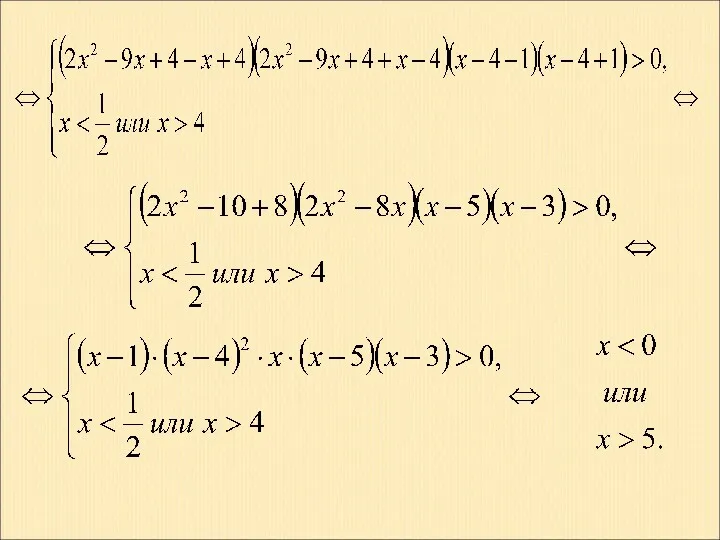


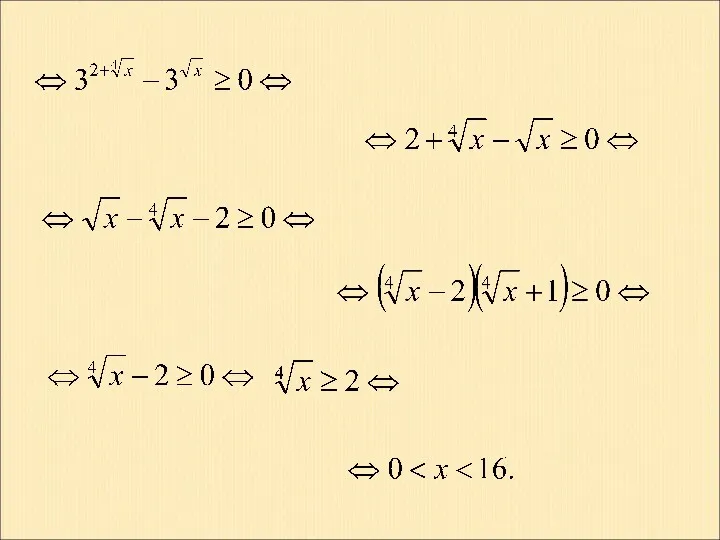



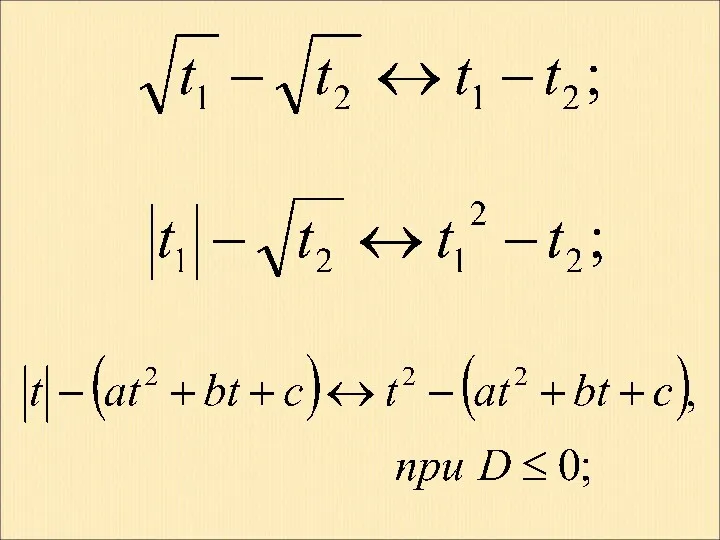
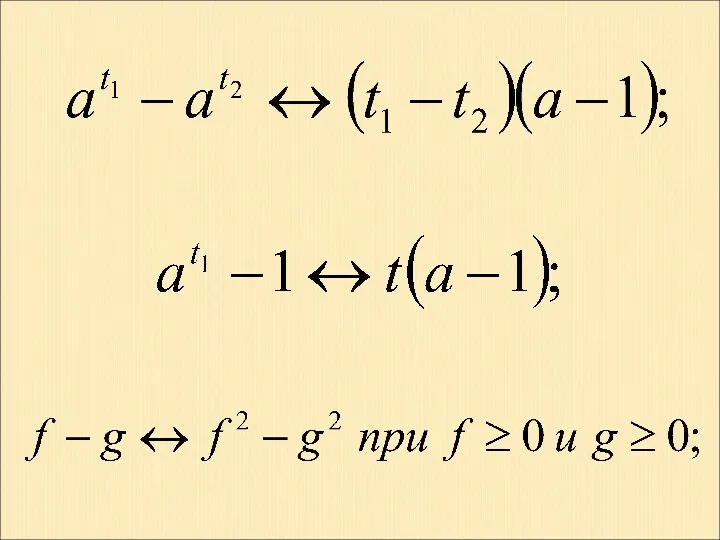
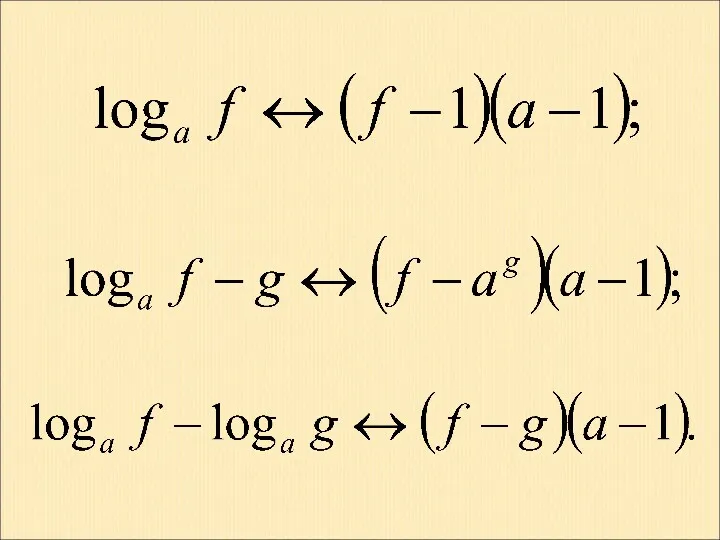
 Симметрия вокруг нас
Симметрия вокруг нас урок Скалярное произведение
урок Скалярное произведение Теория вероятностей
Теория вероятностей Игра Заселяем домики. Состав чисел от 2 до 9
Игра Заселяем домики. Состав чисел от 2 до 9 Минимизация логических функций
Минимизация логических функций Симметрия относительно прямой и мы в мире симметрии
Симметрия относительно прямой и мы в мире симметрии Простейшие преобразования графиков функций
Простейшие преобразования графиков функций Углы в кубе. Расстояния в кубе
Углы в кубе. Расстояния в кубе Занимательная математика
Занимательная математика Применение синквейна на уроках истории и обществознания
Применение синквейна на уроках истории и обществознания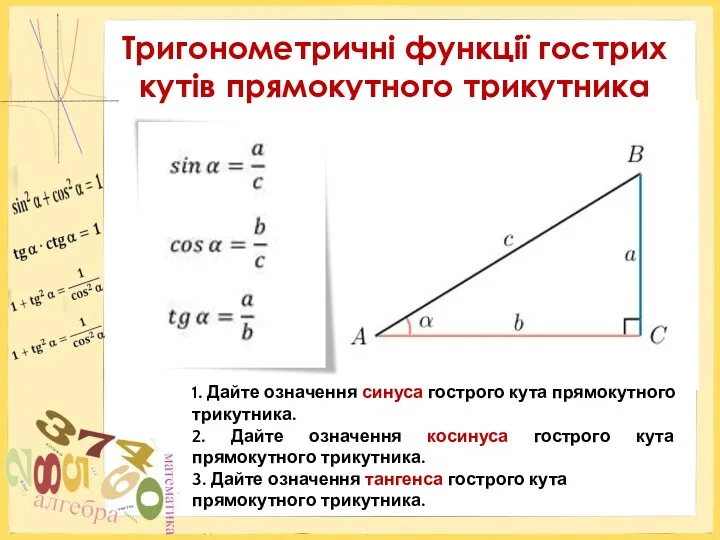 Тригонометричні функції гострих кутів прямокутного трикутника
Тригонометричні функції гострих кутів прямокутного трикутника Дроби. Устный счет
Дроби. Устный счет Элементы комбинаторики. Способы решения комбинаторных задач
Элементы комбинаторики. Способы решения комбинаторных задач Приближенные методы решения определенных интегралов
Приближенные методы решения определенных интегралов Сикһеҙ геометрик прогрессия
Сикһеҙ геометрик прогрессия Конкурсный урок геометрии в 7 классе. Тема урока Треугольники
Конкурсный урок геометрии в 7 классе. Тема урока Треугольники Прием письменного вычитания для случаев вида 7000-456
Прием письменного вычитания для случаев вида 7000-456 Отрицательные числа
Отрицательные числа Прямая на плоскости
Прямая на плоскости Интерактивное пособие по математике 1 класс.Рабочая тетрадь 1 часть (продолжение)
Интерактивное пособие по математике 1 класс.Рабочая тетрадь 1 часть (продолжение) Математический турнир
Математический турнир Презентация Знакомим дошкольника с часами
Презентация Знакомим дошкольника с часами Умножение и деление рациональных чисел
Умножение и деление рациональных чисел Натуральные числа. Урок-сказка
Натуральные числа. Урок-сказка Архангельск в огненные военные...
Архангельск в огненные военные... Определения многогранников. Теорема Эйлера
Определения многогранников. Теорема Эйлера Вписані та описані чотирикутники
Вписані та описані чотирикутники 23. Признак перпендикулярности двух плоскостей
23. Признак перпендикулярности двух плоскостей