Содержание
- 2. Постановка задачи Решить систему нелинейных уравнений:
- 3. Этапы решения Исследовать существование и единственность решения Выбрать начальное приближение к корню Вычислить отдельные корни с
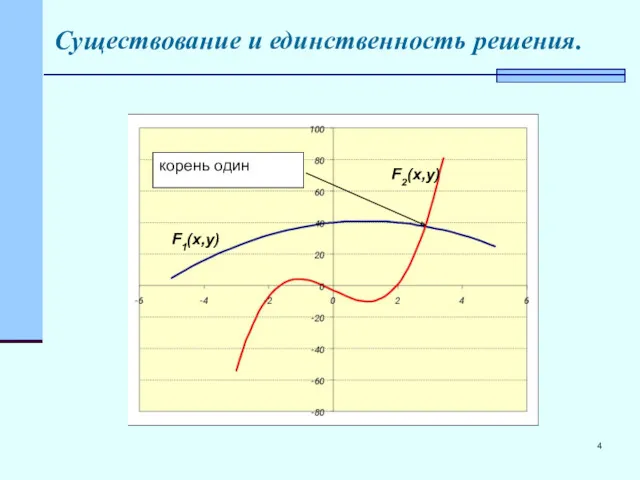
- 4. Существование и единственность решения. корень один F1(x,y) F2(x,y)
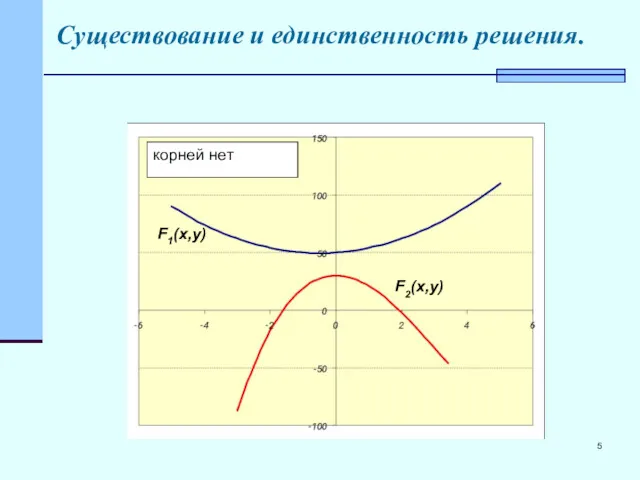
- 5. Существование и единственность решения. корней нет F1(x,y) F2(x,y)
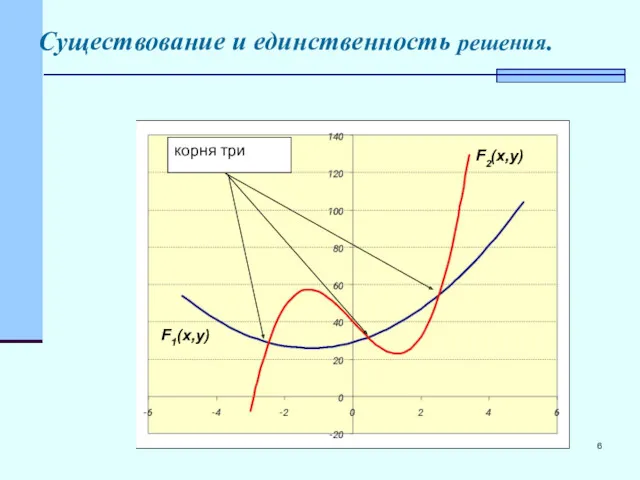
- 6. Существование и единственность решения. корня три F1(x,y) F2(x,y)
- 7. Этап 3 предполагается, что система нелинейных уравнений имеет вещественное решение на заданном интервале Определено начальное приближение
- 8. Для применения известных численных методов исходная система может быть приведена к виду: x=φ1(x,y); y=φ2(x,y); Методы решения
- 9. Алгоритм поиска решения задается формулами xn+1= φ1(xn,yn); yn+1= φ2(xn,yn). Метод Якоби (простых итераций)
- 10. Метод Гаусса - Зейделя Алгоритм поиска решения задается формулами x n+1= φ1(xn,yn); yn+1= φ2(xn+1,yn). Процесс вычисления
- 11. Методы решения систем нелинейных уравнений Общий вид системы нелинейных уравнений: F1(x1, x2, x3, …, xn) =
- 12. Метод Якоби x1m+1 = f1(x1m, x2m, x3m, …, xnm) x2m+1 = f2(x1m, x2m, x3m, …, xnm)
- 13. Метод Гаусса - Зейделя x1m+1 = f1(x1m, x2m, x3m, …, xnm) x2m+1 = f2(x1m+1, x2m, x3m,
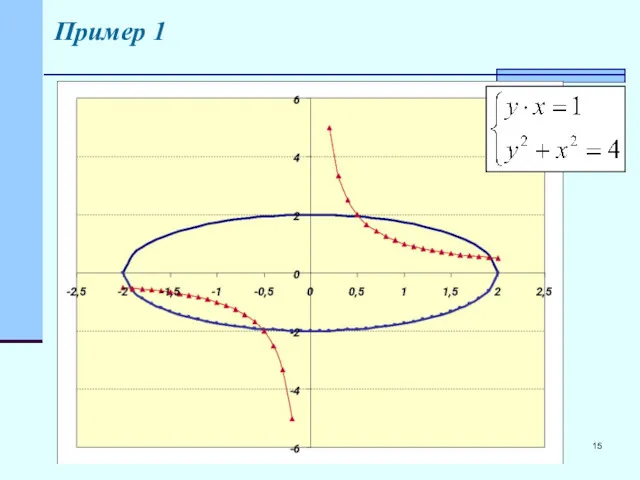
- 14. Пример 1 Дана система Построим графики этих уравнений
- 15. Пример 1
- 16. Пример 1 Приведем систему к виду
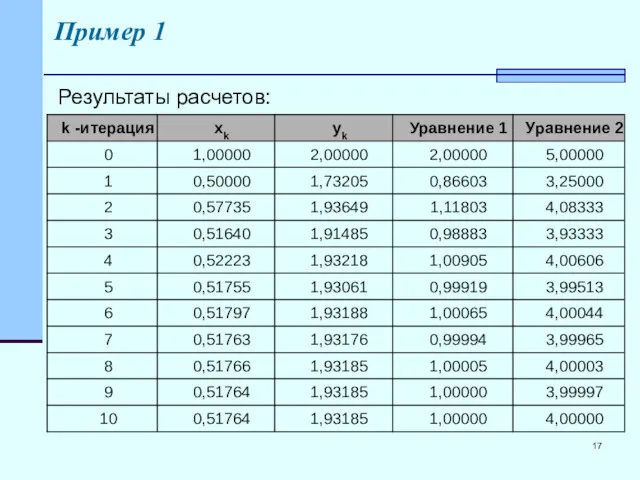
- 17. Пример 1 Результаты расчетов:
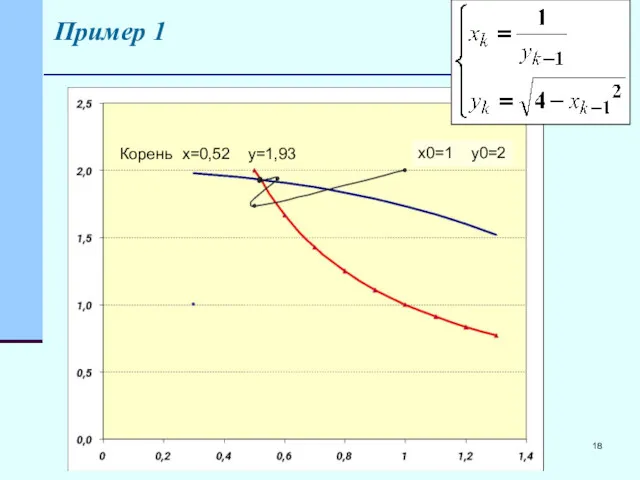
- 18. Пример 1 Корень x=0,52 y=1,93 x0=1 y0=2
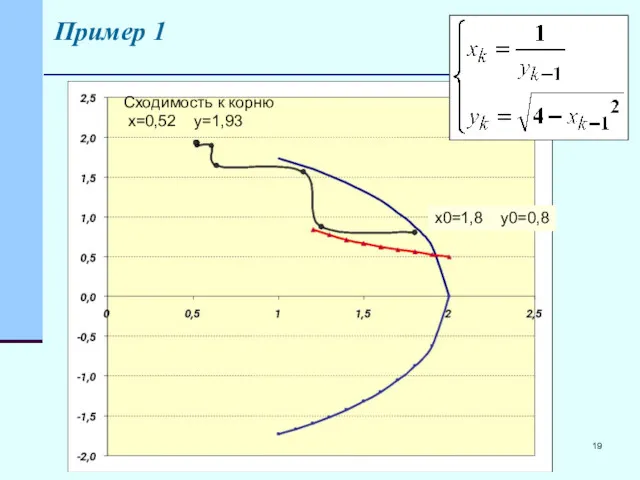
- 19. Пример 1 Сходимость к корню x=0,52 y=1,93 x0=1,8 y0=0,8
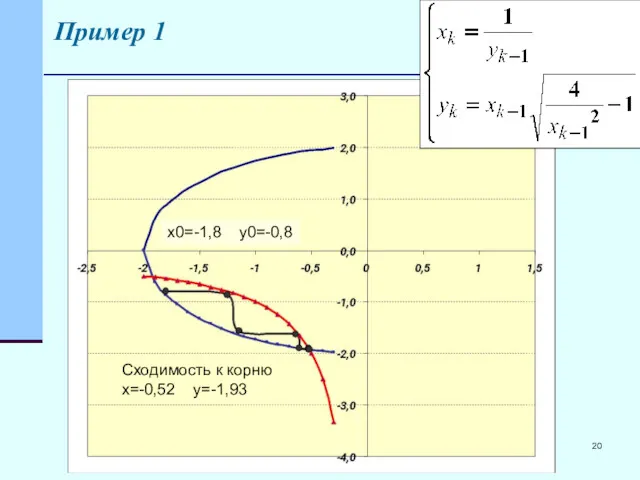
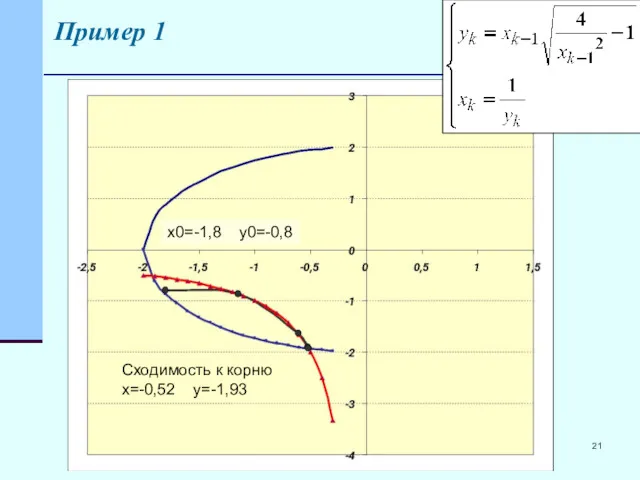
- 20. Пример 1 Сходимость к корню x=-0,52 y=-1,93 x0=-1,8 y0=-0,8
- 21. Пример 1 Сходимость к корню x=-0,52 y=-1,93 x0=-1,8 y0=-0,8
- 22. выводы Вычисления в методе последовательных приближений просты Однако сложно найти такую систему которая была бы эквивалентна
- 23. Метод Ньютона Это точный аналог одномерного метода Ньютона, т.е. одноточечный метод в котором используется производная В
- 24. Метод Ньютона Запишем систему двух уравнений с двумя неизвестными в векторной форме:
- 25. Метод Ньютона Обобщая формулу Ньютона на многомерный случай получим:
- 26. Метод Ньютона
- 27. Операции с матрицами Произведение матрицы и вектора Обратная матрица
- 28. Пример 1 (метод Ньютона) Применим метод к исходной системе
- 29. Пример 1 (метод Ньютона) Найдем матрицу, обратную к матрице производных:
- 30. Пример 1 (метод Ньютона) Окончательно получим итерационную схему
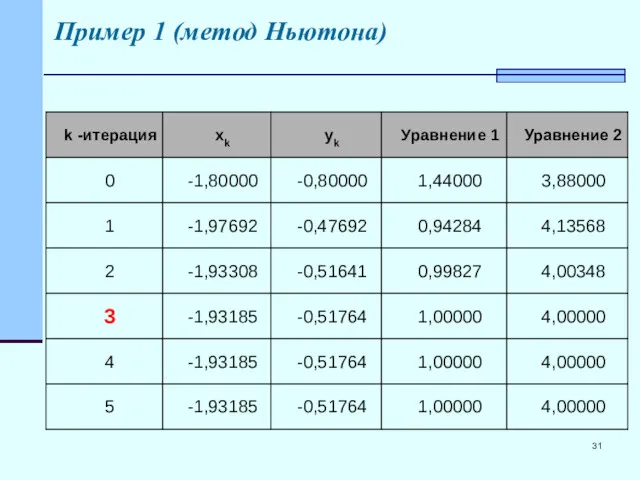
- 31. Пример 1 (метод Ньютона)
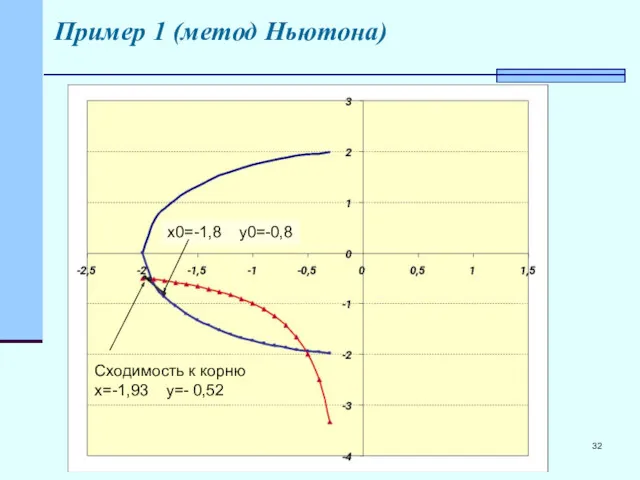
- 32. Пример 1 (метод Ньютона) Сходимость к корню x=-1,93 y=- 0,52 x0=-1,8 y0=-0,8
- 34. Скачать презентацию




















 Математичний пакет Mathematica. Лекція №4
Математичний пакет Mathematica. Лекція №4 Сумма углов треугольника
Сумма углов треугольника Классическая теория вероятности
Классическая теория вероятности Урок-путешествие по сказкам. Математика 2 класс. Умножение 1 и 0
Урок-путешествие по сказкам. Математика 2 класс. Умножение 1 и 0 Случайные события. Вероятность случайного события
Случайные события. Вероятность случайного события Сложение и вычитание десятичных дробей. Математика и природа
Сложение и вычитание десятичных дробей. Математика и природа Конические поверхности. Поверхности вращения
Конические поверхности. Поверхности вращения Ділення двоцифрових чисел на одноцифрове способами розкладання на зручні доданки
Ділення двоцифрових чисел на одноцифрове способами розкладання на зручні доданки Табличные случаи умножения и деления
Табличные случаи умножения и деления Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Взаємне розміщення площини і кулі у просторі
Взаємне розміщення площини і кулі у просторі Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Все правила, изучающие в начальной школе
Все правила, изучающие в начальной школе Презентация к уроку: Тема Геометрические тела. Шар. Куб.( математика 1 класс)
Презентация к уроку: Тема Геометрические тела. Шар. Куб.( математика 1 класс) Перевод обыкновенной дроби в десятичную
Перевод обыкновенной дроби в десятичную Инновационный подход к актуализации экологического компонента в математике
Инновационный подход к актуализации экологического компонента в математике Проценты. Игра Крестики-нолики
Проценты. Игра Крестики-нолики Выражения с дробями
Выражения с дробями Палочки Кюизенера как средство развития математических способностей дошкольников.
Палочки Кюизенера как средство развития математических способностей дошкольников. Пирамида
Пирамида Случаи сложения вида +5
Случаи сложения вида +5 Урок математики в 3 классе. По теме: Площадь фигур. Симметричные фигуры. Таблица умножения на 8 и 9.
Урок математики в 3 классе. По теме: Площадь фигур. Симметричные фигуры. Таблица умножения на 8 и 9. Решение простейших тригонометрических уравнений - 2
Решение простейших тригонометрических уравнений - 2 Определители и их свойства. Лекция 2
Определители и их свойства. Лекция 2 Область определения функции
Область определения функции Суждение. Суждение, как форма мышления
Суждение. Суждение, как форма мышления Нумерация_1000
Нумерация_1000 Числа и цифры 8, 9. Письмо цифры 8 . УМК Школа России
Числа и цифры 8, 9. Письмо цифры 8 . УМК Школа России