Содержание
- 2. Комплексным числом называется выражение вида а + bi, в котором а и b – действительные числа,
- 3. Два комплексных числа (a; b) и (c; d) называются равными, если а = с и b
- 4. Арифметические операции над комплексными числами Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида
- 5. Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z2/z1= (a+bi)/(c+di)= (ac+bd)/(c2+d2)+(bc−ad)*i /(c2+d2)
- 6. Нахождение степеней числа i Если показатель степени i делится на 4, то значение степени равно 1,
- 7. Вычислить: 1) i 66 , 2) i143 , 3) i216 ,4)i137 Решение: 1) i66 66:4=16(2). Остаток
- 8. Пример 1 Вычислить:
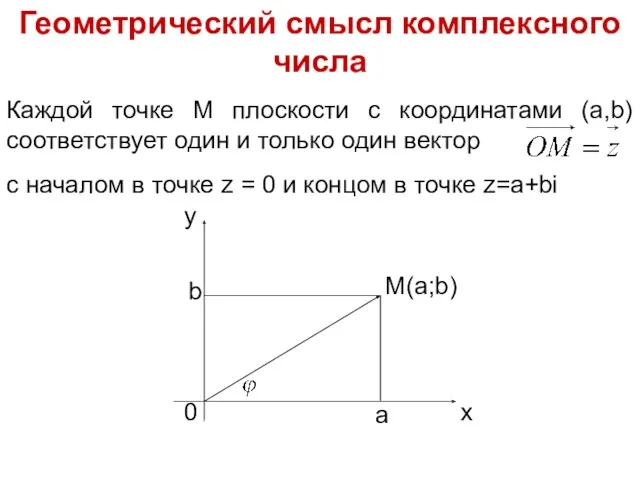
- 10. Геометрический смысл комплексного числа Каждой точке М плоскости с координатами (a,b) соответствует один и только один
- 11. Если комплексное число Z= a+bi трактовать как точку M (a,b) плоскости xOy, то модуль Z равен
- 12. Тригонометрическая форма комплексного числа Тригонометрической формой комплексного числа называют его запись в виде: z = r(cosφ
- 13. Пример2. Записать в тригонометрической форме: Сначала находим модуль числа: Далее, согласно формулам (*), имеем: Учитывая, что
- 14. Действия над комплексными числами, заданными в тригонометрической форме При умножении/делении комплексных чисел, заданных в тригонометрической форме,
- 15. Пример3. Выполнить действия: Используя формулу (1), находим:
- 16. При возведении комплексного числа z = r (Cosφ + iSinφ) в натуральную степень n модуль данного
- 17. Корень n-й степени из комплексного числа z = r (Cosφ + iSinφ) имеет n различных значений,
- 18. Пример4. Решить уравнение Корнями данного уравнения являются все значения Для числа - 4 имеем r =2,
- 19. Показательная форма комплексного числа. Формула Эйлера Если комплексному числу , модуль которого равен 1, поставить в
- 20. Пример: Записать число в показательной форме. Решение: Здесь тогда показательная форма числа имеет вид .
- 21. Пример: Записать число в показательной форме. Решение. Что бы представить число в виде нужно найти модуль
- 22. Действия над комплексными числами, заданными в показательной форме Если комплексные числа записаны в показательной форме, то
- 23. Для вычисления корня из комплексного числа используется формула где k принимает n значений: 0,1,2,…,n-1.
- 24. Понятие функции комплексного переменного и отличие от действительного анализа Пусть D – некоторая область на комплексной
- 25. - n-значная функция; -бесконечнозначная функция. Если функция однозначна,то она может быть задана в виде отображения В
- 26. Пример: Для функции найти Решение: Подставим в место z значение i в функцию Ответ: f(i)=1
- 27. Компоненты функции Пусть дана функция , Представим z в алгебраической форме Значение f(x)-комплексное число,т.е. ,которое также
- 28. Пример: Для функции Где найти ее действительную и мнимую часть. Решение: (x+iy)2+4i=x2+2ixy-y2+4i=(x2-y2)+(2xyi+4i)=(x2-y2)+i(2xy+4). Тогда действительная часть функции
- 30. Скачать презентацию







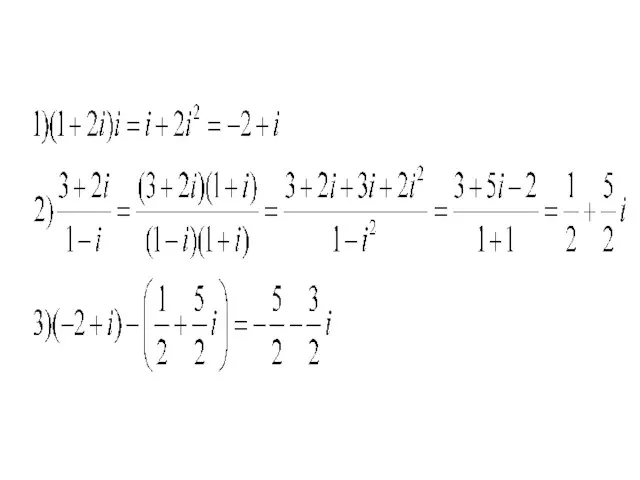


















 Сравнение и измерение отрезков. 7 класс
Сравнение и измерение отрезков. 7 класс История космонавтики в цифрах
История космонавтики в цифрах Тренажер Нумерация чисел в пределах 100 2 класс
Тренажер Нумерация чисел в пределах 100 2 класс Нахождение числа по его процентам
Нахождение числа по его процентам Абсолютные и относительные показатели. Статистика, тема 6
Абсолютные и относительные показатели. Статистика, тема 6 Обобщение и систематизация знаний по теме десятичные дроби
Обобщение и систематизация знаний по теме десятичные дроби Древние системы счисления в современном мире
Древние системы счисления в современном мире Задачі на визначення, на скільки коротший. Обчислення значень виразів
Задачі на визначення, на скільки коротший. Обчислення значень виразів Презентация к уроку математики Целое и часть Диск
Презентация к уроку математики Целое и часть Диск Теория поверхностей. Касательная плоскость поверхности. Нормаль
Теория поверхностей. Касательная плоскость поверхности. Нормаль Задачи по математике
Задачи по математике Умножение и деление обыкновенной дроби на натуральное число
Умножение и деление обыкновенной дроби на натуральное число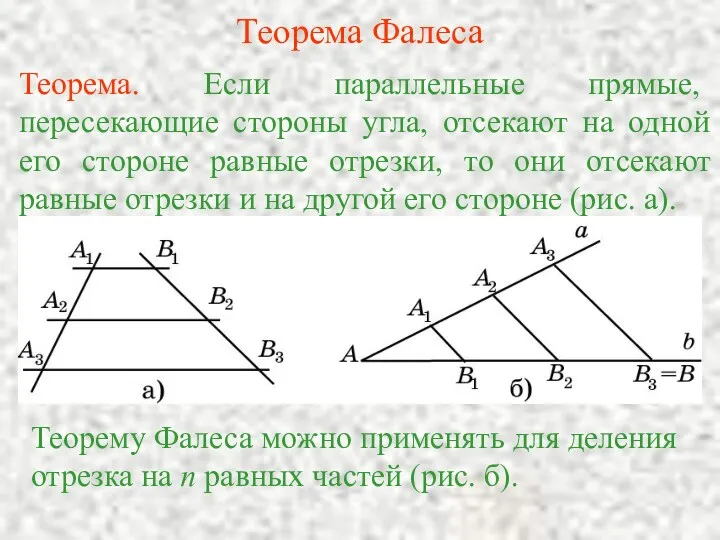 Теорема Фалеса
Теорема Фалеса Переместительное свойство умножения
Переместительное свойство умножения Производная функции в точке
Производная функции в точке Графическая работа. Следствия из аксиом стереометрии
Графическая работа. Следствия из аксиом стереометрии Интеллектуальная игра Великие математики
Интеллектуальная игра Великие математики Презентация к уроку математики Проверка деления с остатком и обобщение знаний об историческом летосчислении
Презентация к уроку математики Проверка деления с остатком и обобщение знаний об историческом летосчислении Презентация к уроку о Великой Отечественной войне
Презентация к уроку о Великой Отечественной войне Предикаты и формулы. Интерпретации. Истинность и выполнимость формул. Нормальные формы. (Лекция 3-4)
Предикаты и формулы. Интерпретации. Истинность и выполнимость формул. Нормальные формы. (Лекция 3-4) Задачи на нахождение дроби от числа и числа по его части. Математика. 5 класс
Задачи на нахождение дроби от числа и числа по его части. Математика. 5 класс интерактивный тренажёр Вычитание в пределах 20
интерактивный тренажёр Вычитание в пределах 20 Презентация к интегрированному уроку Математика и окружающий мир.
Презентация к интегрированному уроку Математика и окружающий мир. Математика о вреде курения. 6 класс
Математика о вреде курения. 6 класс Игра-тренажёр На стройке. 1 класс
Игра-тренажёр На стройке. 1 класс Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения
Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения Теорема Пифагора и неизвестные способы ее доказательства
Теорема Пифагора и неизвестные способы ее доказательства Трикутники. Види трикутників. Казка (математика 5 клас)
Трикутники. Види трикутників. Казка (математика 5 клас)