Содержание
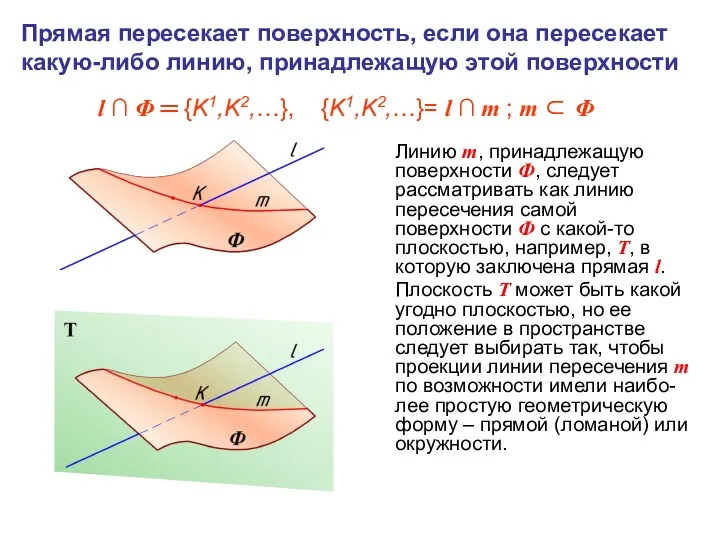
- 2. Пересечение прямой линии с поверхностью
- 3. Линию m, принадлежащую поверхности Ф, следует рассматривать как линию пересечения самой поверхности Ф с какой-то плоскостью,
- 4. 1. Прямую l заключаем в плоскость Т (l ∪Т) с условием, что Т ∩ Φ =
- 5. Пересечение прямой линии с плоскостью
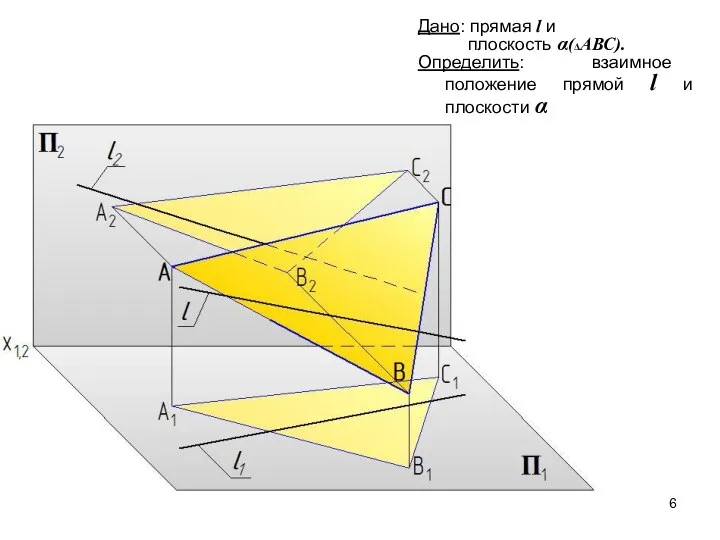
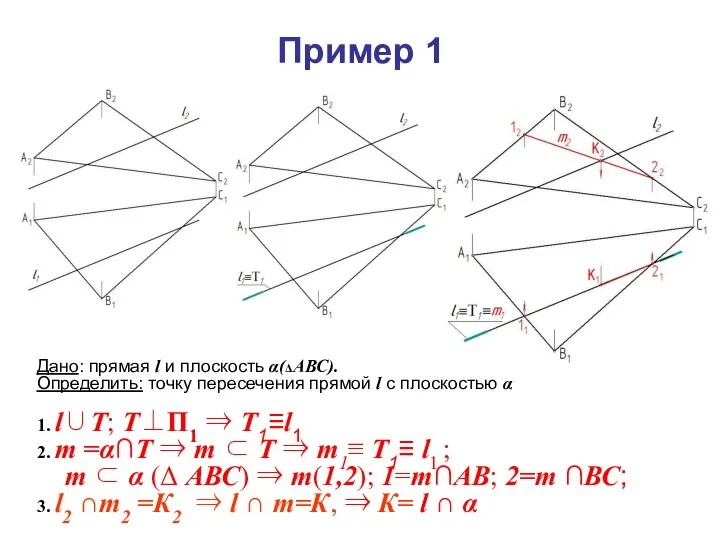
- 6. Дано: прямая l и плоскость α(ΔАВС). Определить: взаимное положение прямой l и плоскости α
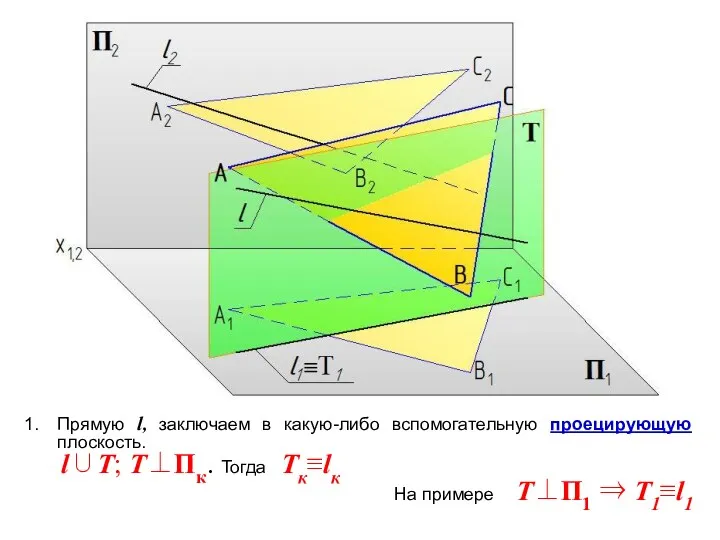
- 7. Прямую l, заключаем в какую-либо вспомогательную проецирующую плоскость. l∪Т; Т⊥Пк. Тогда Тк≡lк На примере Т⊥П1 ⇒
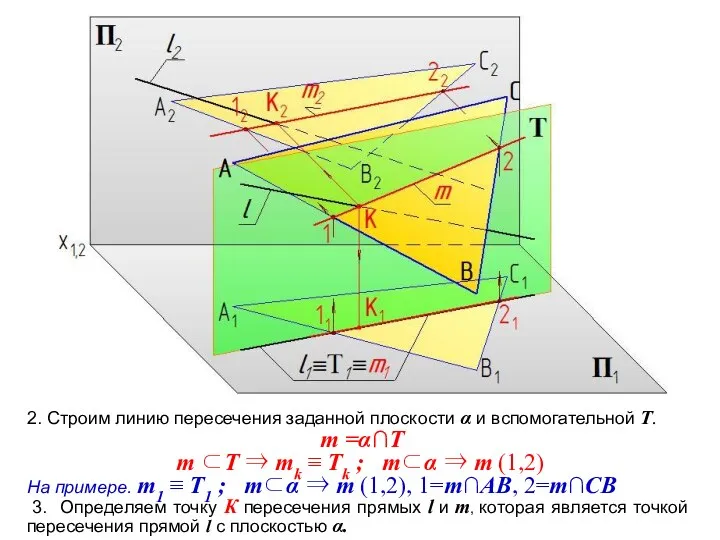
- 8. 2. Строим линию пересечения заданной плоскости α и вспомогательной Т. m =α∩T m ⊂T ⇒ mk
- 9. Решение рассмотренной задачи на эпюре
- 10. Дано: прямая l и плоскость α(ΔАВС). Определить: точку пересечения прямой l с плоскостью α 1. l∪Т;
- 11. Пересечение прямой линии с гранной поверхностью (на примере пирамидальной поверхности)
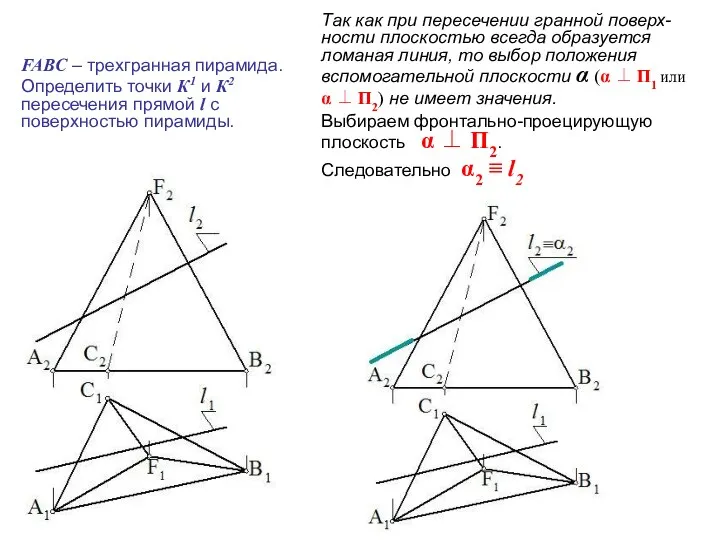
- 12. FABC – трехгранная пирамида. Определить точки К1 и К2 пересечения прямой l с поверхностью пирамиды. Так
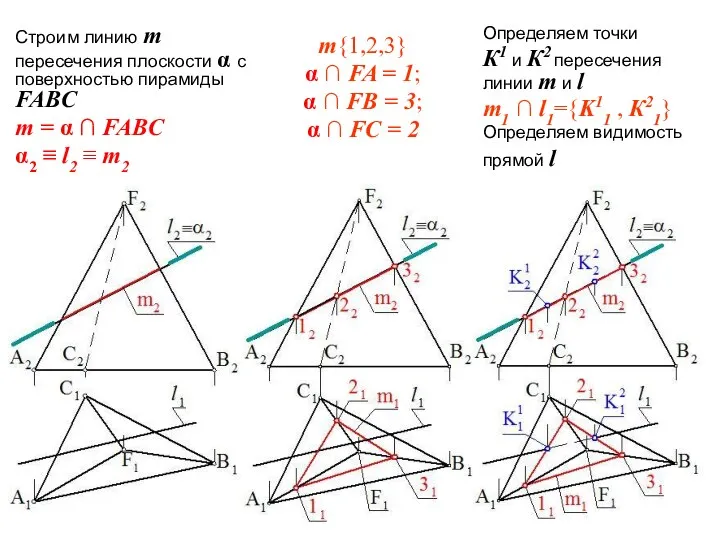
- 13. Строим линию m пересечения плоскости α с поверхностью пирамиды FABC m = α ∩ FABC α2
- 14. Пересечение прямой линии с конической поверхностью
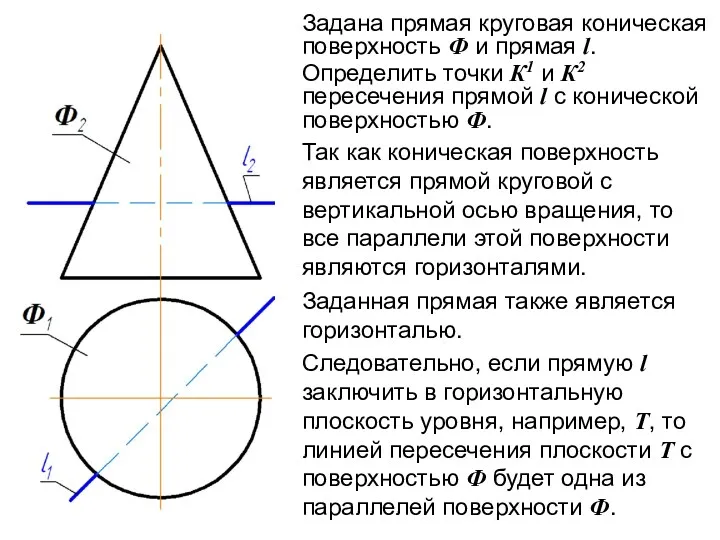
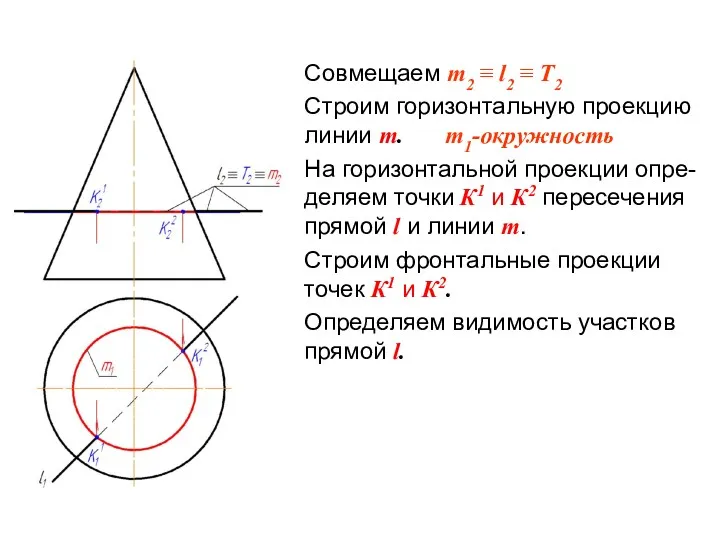
- 15. Задана прямая круговая коническая поверхность Ф и прямая l. Определить точки К1 и К2 пересечения прямой
- 16. Совмещаем m2 ≡ l2 ≡ Т2 Строим горизонтальную проекцию линии m. m1-окружность На горизонтальной проекции опре-деляем
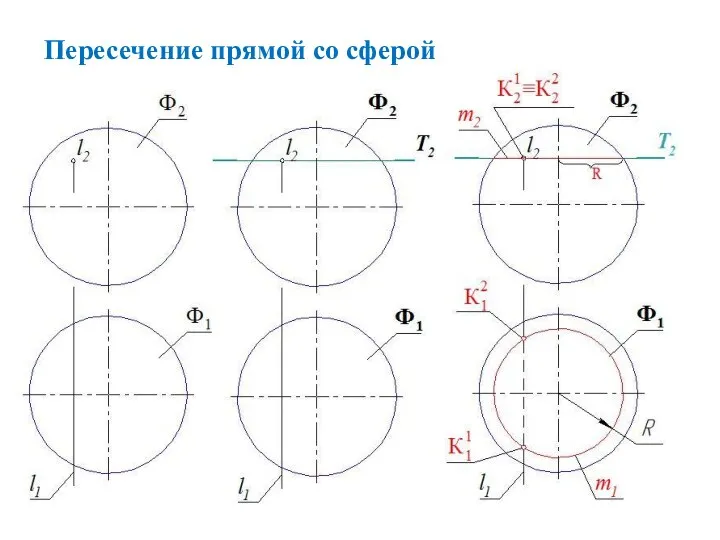
- 17. Пересечение прямой со сферой
- 18. Взаимное пересечение поверхностей
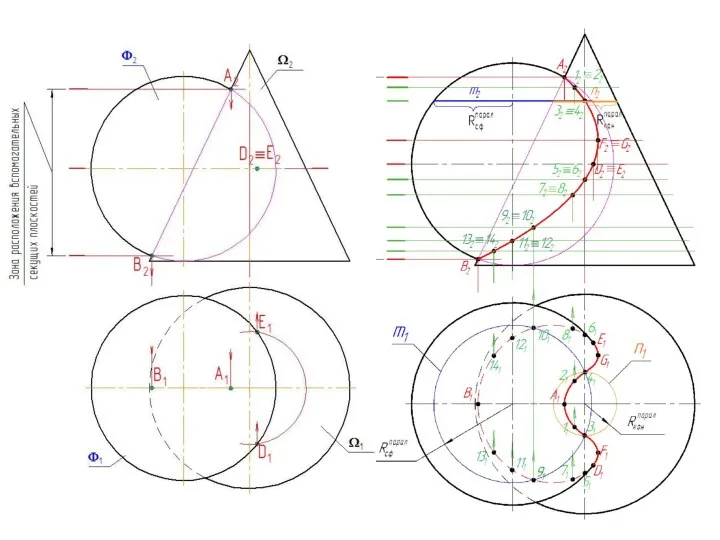
- 19. Метод вспомогательных секущих плоскостей
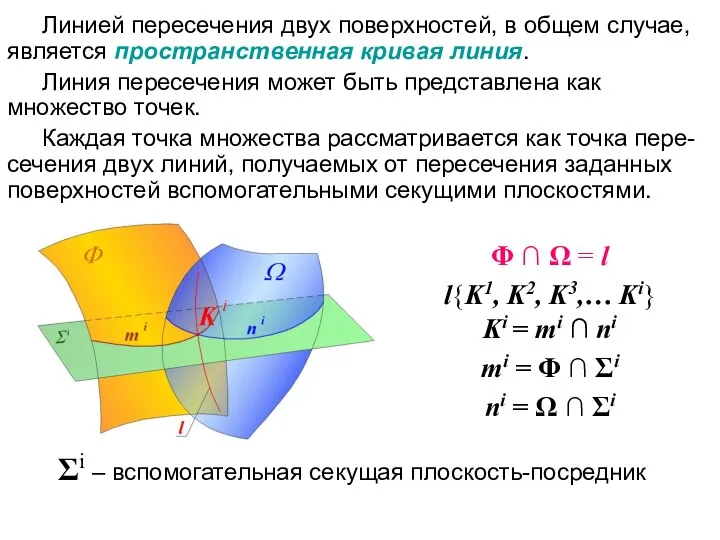
- 20. Линией пересечения двух поверхностей, в общем случае, является пространственная кривая линия. Линия пересечения может быть представлена
- 21. Обязательные требования, предъявляемые к секущим плоскостям: каждая из секущих плоскостей должна пересекать обе заданные поверхности; линии,
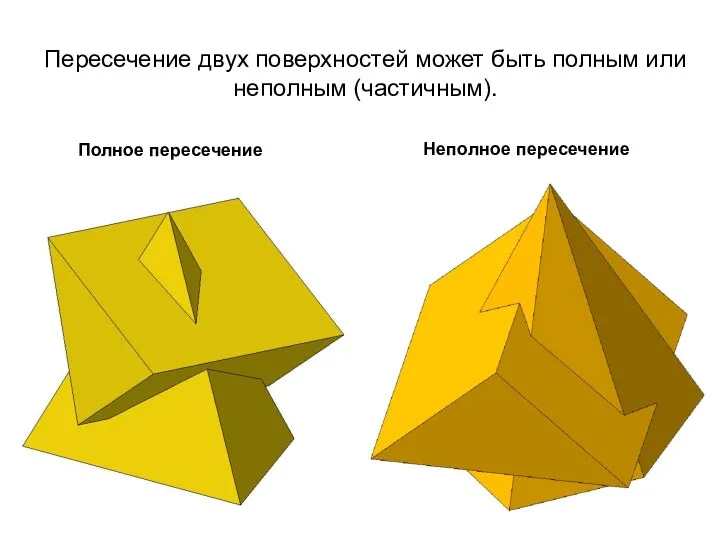
- 22. Полное пересечение Неполное пересечение Пересечение двух поверхностей может быть полным или неполным (частичным).
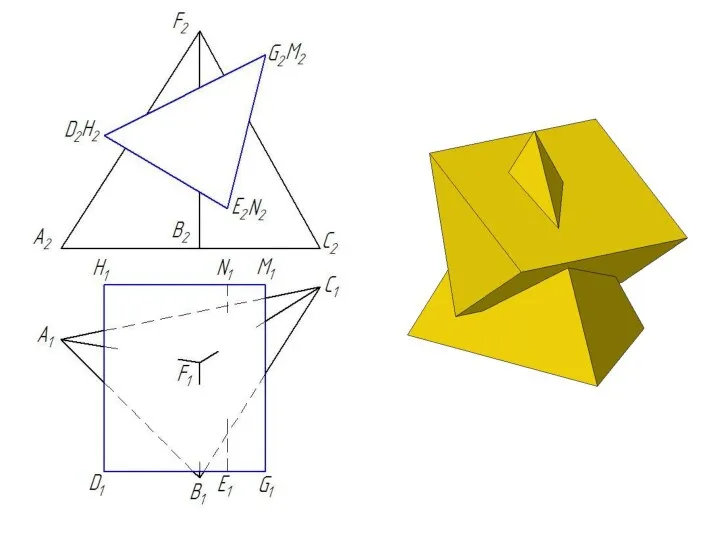
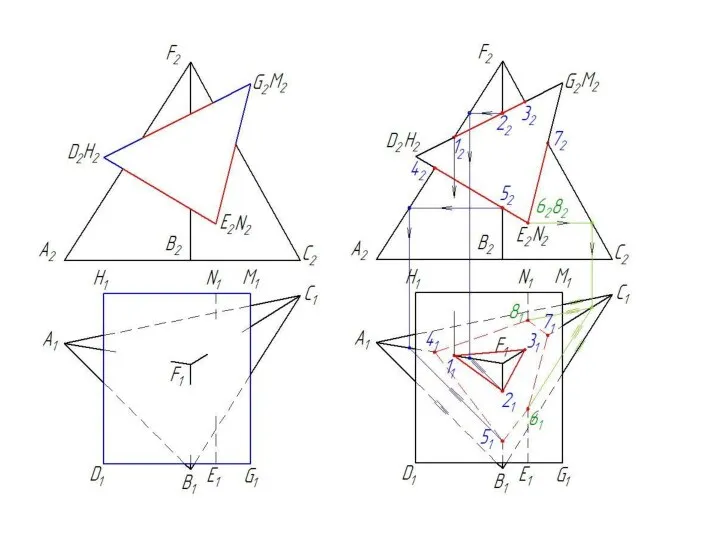
- 23. Взаимное пересечение двух гранных поверхностей Линией пересечения двух гранных поверхностей является ломаная прямая линия, точками излома
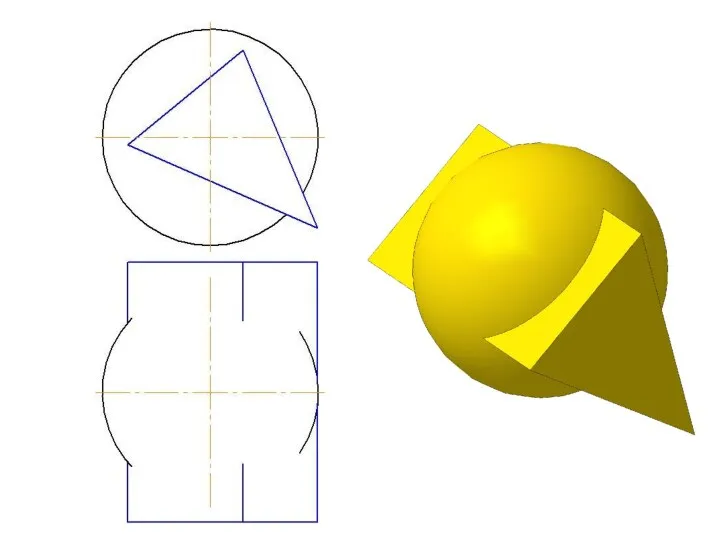
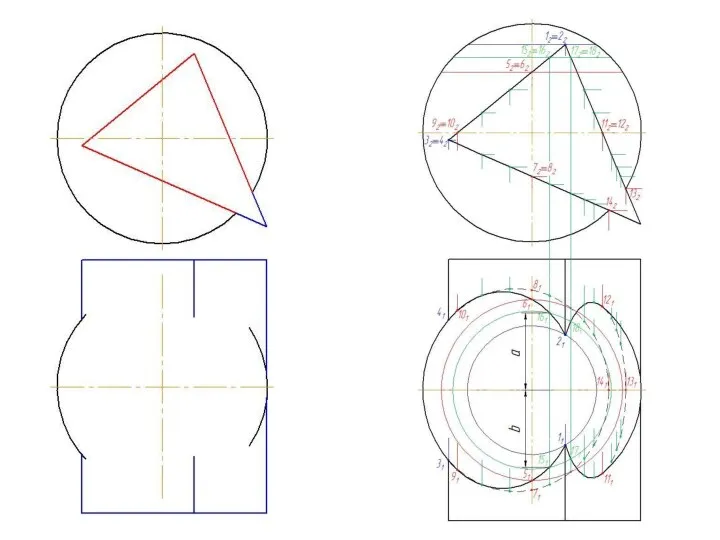
- 26. Взаимное пересечение гранной поверхности с кривой поверхностью Линия пересечения гранной поверхности с кривой поверхностью представляет собой
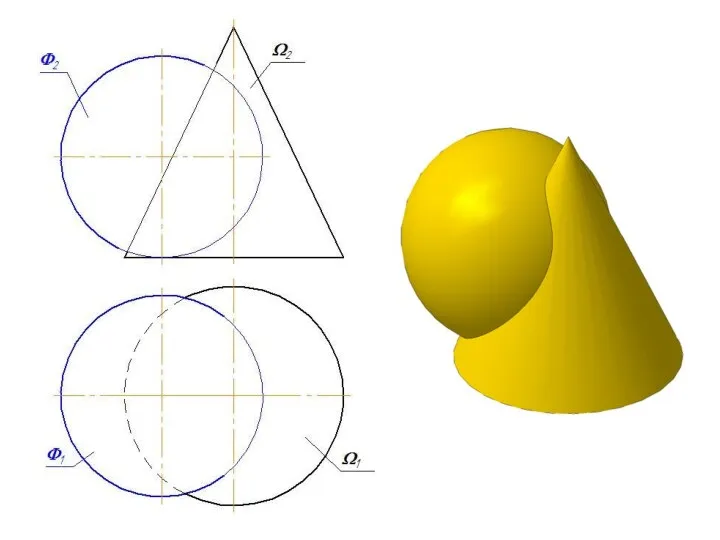
- 29. Взаимное пересечение кривых поверхностей
- 32. Частные случаи взаимного пересечения двух поверхностей вращения
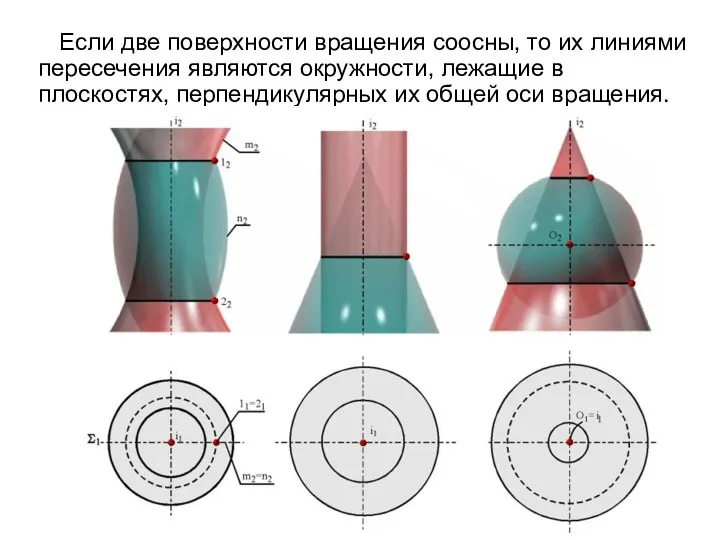
- 33. Если две поверхности вращения соосны, то их линиями пересечения являются окружности, лежащие в плоскостях, перпендикулярных их
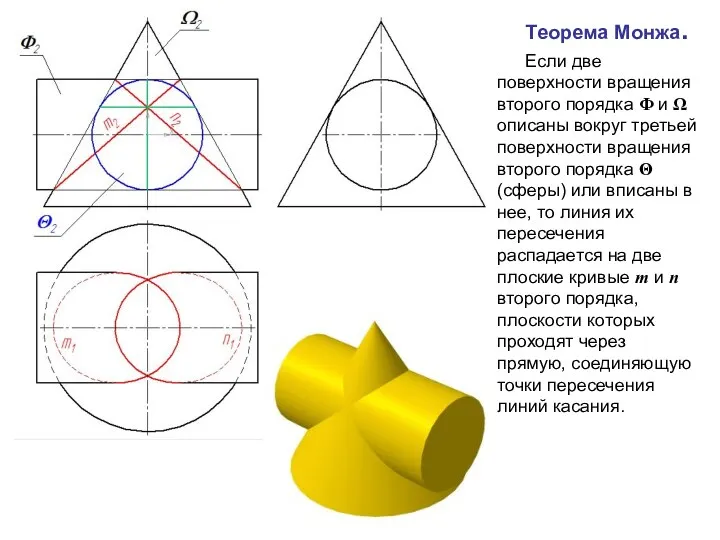
- 34. Теорема Монжа. Если две поверхности вращения второго порядка Φ и Ω описаны вокруг третьей поверхности вращения
- 36. Скачать презентацию













 Название компонентов и результата действия деления
Название компонентов и результата действия деления Умножение и деление степеней
Умножение и деление степеней Математика в системі інших наук
Математика в системі інших наук Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера В гостях у сказки (задачи на пропорции). 6 класс
В гостях у сказки (задачи на пропорции). 6 класс Презентация Играем и учимся со счетными палочками
Презентация Играем и учимся со счетными палочками Отношение величин
Отношение величин Урок по математике для учащихся 1 класса Сложение с числом 0
Урок по математике для учащихся 1 класса Сложение с числом 0 Натуральные числа
Натуральные числа Всё о треугольниках
Всё о треугольниках Математика Тема: Королевство математики
Математика Тема: Королевство математики Презентация и конспект урока Решение уравнений 3 класс УМК 2100
Презентация и конспект урока Решение уравнений 3 класс УМК 2100 Умножение десятичной дроби на натуральное число
Умножение десятичной дроби на натуральное число Высказывания с кванторами в начальном курсе математики
Высказывания с кванторами в начальном курсе математики Табличное умножение и деление, сложение и вычитание. Тренажёр
Табличное умножение и деление, сложение и вычитание. Тренажёр Вычитание с переходом через десяток
Вычитание с переходом через десяток Законы арифметических действий
Законы арифметических действий Решение задач по теме Правильный многоугольник
Решение задач по теме Правильный многоугольник Квадратичная функция и её график. 9 класс
Квадратичная функция и её график. 9 класс Найди цифры
Найди цифры Математическая игра Смекай, отгадывай, считай
Математическая игра Смекай, отгадывай, считай Рационал сандарды көбейту
Рационал сандарды көбейту Презентация к уроку математики по программе Перспективная начальная школа
Презентация к уроку математики по программе Перспективная начальная школа Избранные главы математики
Избранные главы математики Сравнение чисел
Сравнение чисел Закон больших чисел
Закон больших чисел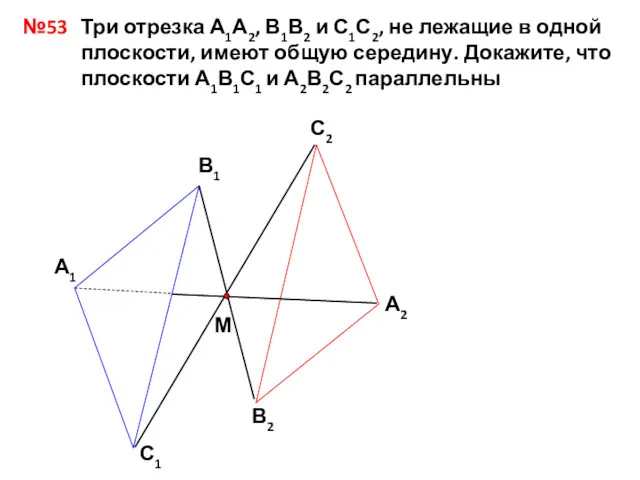 Задачи по геометрии 10 класс
Задачи по геометрии 10 класс Методы теории игр
Методы теории игр