Содержание
- 2. 1.1. Первообразная функция ОПР. Функция называется первообразной для функции на данном промежутке (a;b), если для любого
- 3. Теорема 1.1. Если функция f(x) непрерывна на данном интервале, то на этом интервале она имеет первообразную.
- 4. где – произвольная постоянная. ОПР. Совокупность всех первообразных для данной функции называется ее неопределенным интегралом и
- 5. Знак называется интегралом, функция – подынтегральной функцией, – подынтегральным выражением, Операция нахождения неопределенного интеграла для данной
- 6. 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению: Основные свойства неопределенного интеграла
- 7. 2. Производная неопределенного интеграла равна подынтегральной функции: Таким образом, правильность интегрирования проверяется дифференцированием!
- 8. 3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
- 9. 4. Постоянный множитель можно выносить за знак интеграла:
- 10. 5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых
- 11. 6. Если то где − произвольная функция, имеющая непрерывную производную. Данное свойство называется инвариантностью неопределенного интеграла.
- 12. При вычислении неопределенного интеграла используют формулу:
- 13. Таблица простейших интегралов
- 15. Вычисление интегралов с помощью преобразования подынтегрального выражения к табличной форме и использования свойств неопределенного интеграла называется
- 16. Пример 1. Используя таблицу и свойства интегралов, найти интегралы.
- 19. Непосредственное интегрирование Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и
- 20. При сведении данного интеграла к табличному часто используется следующее преобразование дифференциала (операция «подведения под знак дифференциала»).
- 21. Примеры
- 23. Метод замены переменной (метод подстановки) состоит в преобразовании интеграла в другой интеграл который вычисляется проще, чем
- 24. Пример
- 27. Интегрирование по частям Формула где и – дифференцируемые функции, называется формулой интегрирования по частям. Метод интегрирования
- 28. Некоторые типы интегралов, которые можно вычислять методом интегрирования по частям Интегралы вида где − многочлен, m
- 29. 2. Интегралы вида Здесь полагают за u обозначают остальные сомножители. 3. Интегралы вида где a и
- 31. Скачать презентацию






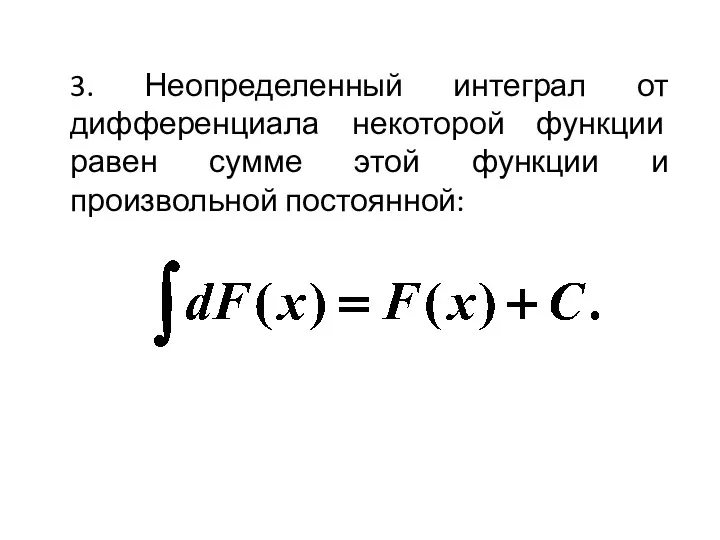





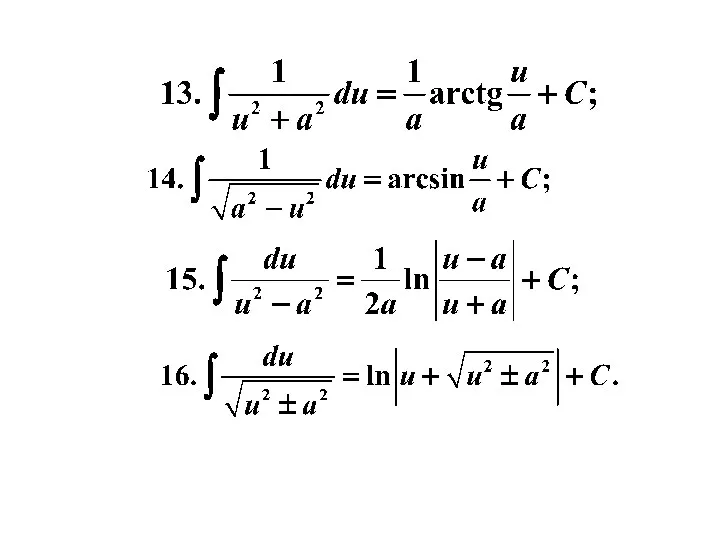


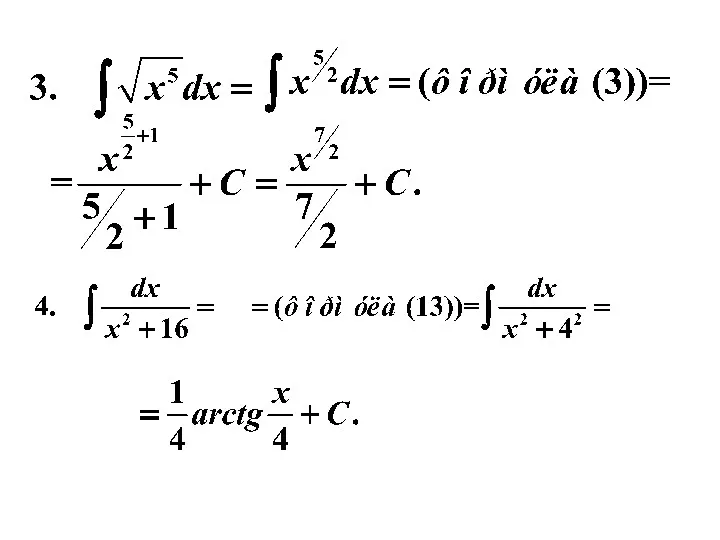
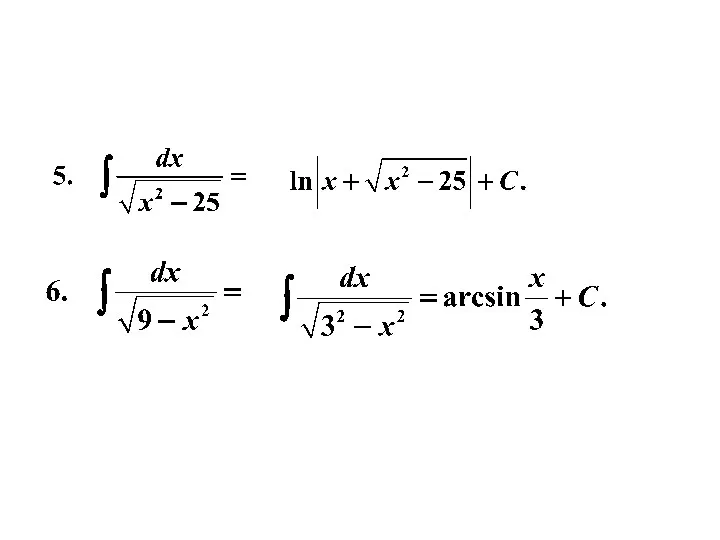


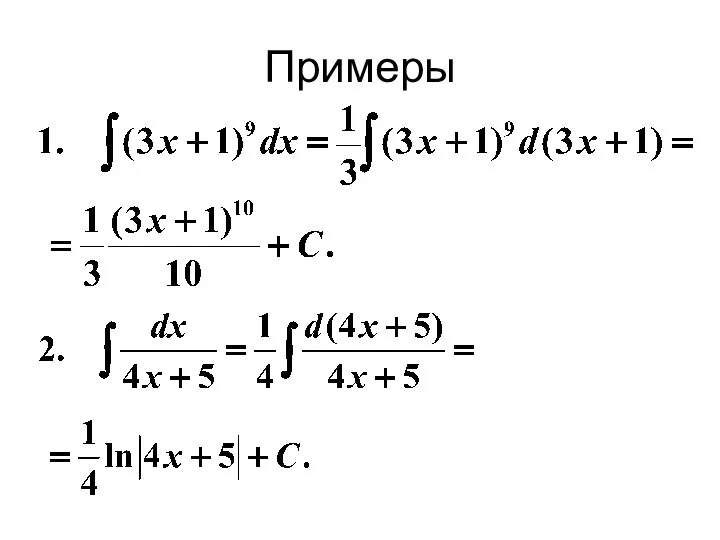
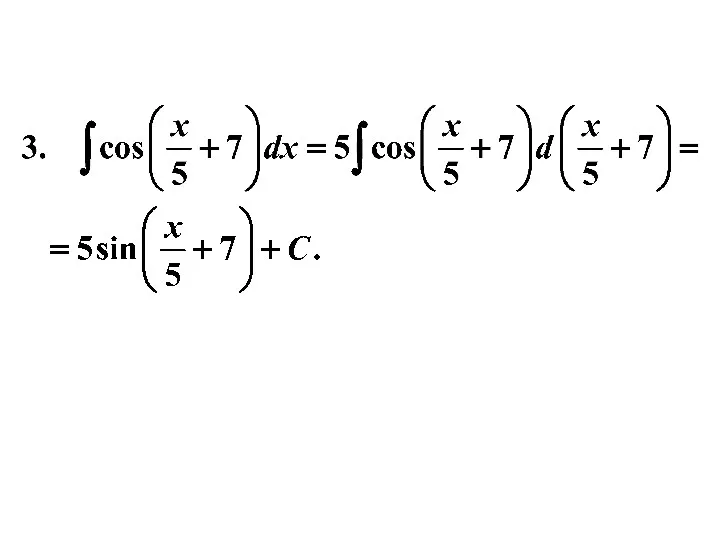

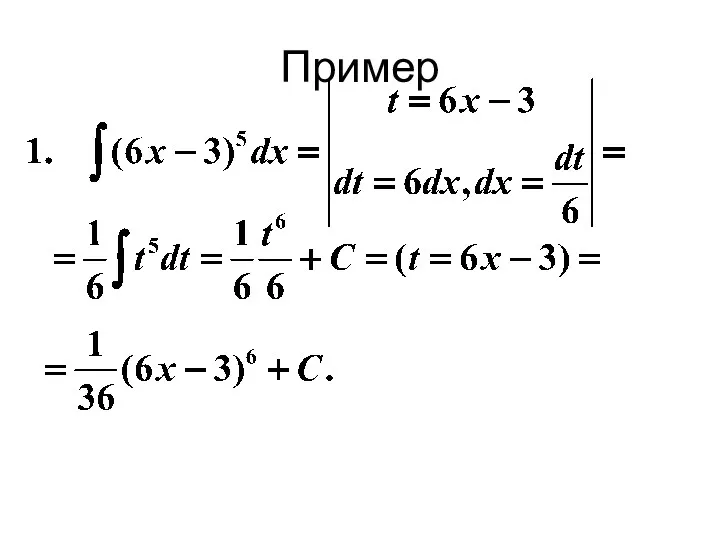
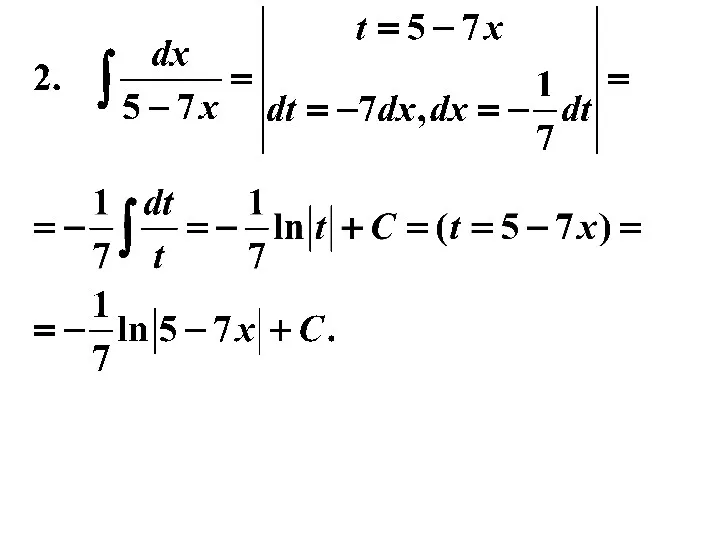
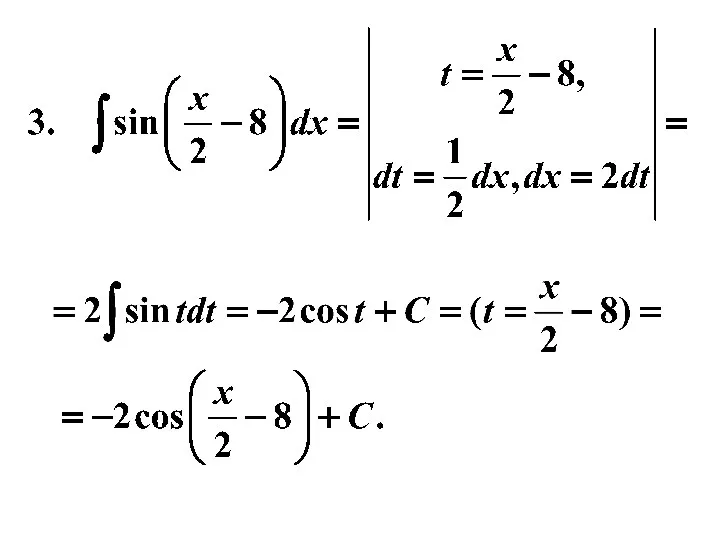



 Геометрические фигуры
Геометрические фигуры Компоненты действия деление
Компоненты действия деление Презентация к технологической карте по математике на тему Умножение многозначного числа на однозначное
Презентация к технологической карте по математике на тему Умножение многозначного числа на однозначное Занимательно о математике. Древняя нумерация. Старинные меры длины. Интересные цифры
Занимательно о математике. Древняя нумерация. Старинные меры длины. Интересные цифры Ознакомление детей младшего возраста с общими математическими понятиями
Ознакомление детей младшего возраста с общими математическими понятиями Уравнение плоскости (профильный уровень), урок №2. 11 класс
Уравнение плоскости (профильный уровень), урок №2. 11 класс Презентация Организация исследовательской работы учащихся
Презентация Организация исследовательской работы учащихся Представление статистических данных: таблицы и графики. Тема 4
Представление статистических данных: таблицы и графики. Тема 4 Линейная функция и её график
Линейная функция и её график Занимательная математика. Собери поговорки для 3 класса
Занимательная математика. Собери поговорки для 3 класса Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1)
Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1) Название компонентов действий
Название компонентов действий Математические исследования ЭЧ электростанций и инженерное проектирование с ЭВМ
Математические исследования ЭЧ электростанций и инженерное проектирование с ЭВМ Единицы измерения
Единицы измерения Кто хочет стать миллионером?
Кто хочет стать миллионером? Логика высказываний
Логика высказываний Виды треугольников
Виды треугольников Сложение чисел с переходом через десяток в пределах 20. Игра-тренажёр
Сложение чисел с переходом через десяток в пределах 20. Игра-тренажёр Создание проблемных ситуаций в процессе формирования ЭМП как средство развития логического мышления.
Создание проблемных ситуаций в процессе формирования ЭМП как средство развития логического мышления. Решение простейших задач по теории вероятности
Решение простейших задач по теории вероятности Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Повторение знаний о нумерации. Числа от 11 до 20
Повторение знаний о нумерации. Числа от 11 до 20 Презентация к уроку математики во 2 классе на тему: Письменный приём вычитания в случаях вида: 40 - 8, УМК Школа России.
Презентация к уроку математики во 2 классе на тему: Письменный приём вычитания в случаях вида: 40 - 8, УМК Школа России. Теория графов
Теория графов Учим состав чисел со Смешариками
Учим состав чисел со Смешариками Математическая игра Слабое звено
Математическая игра Слабое звено Метрология и теория измерений. Погрешности измерений и средств измерений
Метрология и теория измерений. Погрешности измерений и средств измерений презентация Виды углов Диск
презентация Виды углов Диск