Содержание
- 2. План лекции: Актуальность темы Описательная статистика для признаков, не подчиняющихся нормальному закону распределения. Непараметрические критерии достоверности
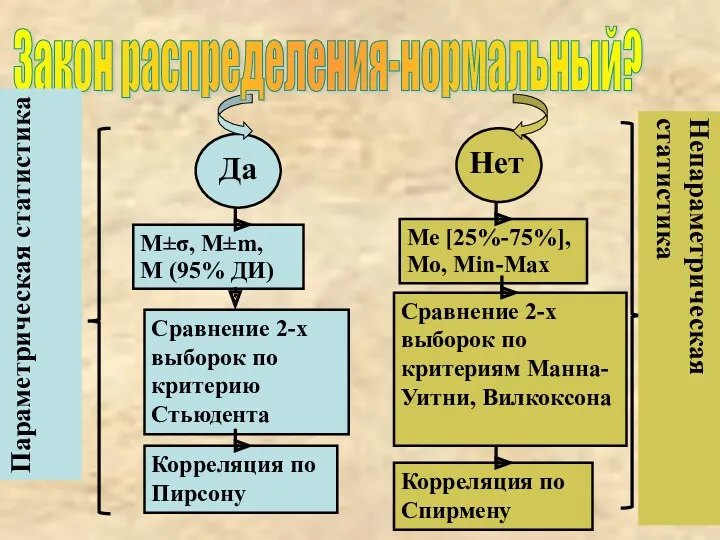
- 3. Да Нет Закон распределения-нормальный? М±σ, М±m, M (95% ДИ) Сравнение 2-х выборок по критерию Стьюдента Корреляция
- 4. Актуальность темы Параметрические методы статистики – совокупность методов проверки статистических гипотез, основывающиеся на знании свойств генеральных
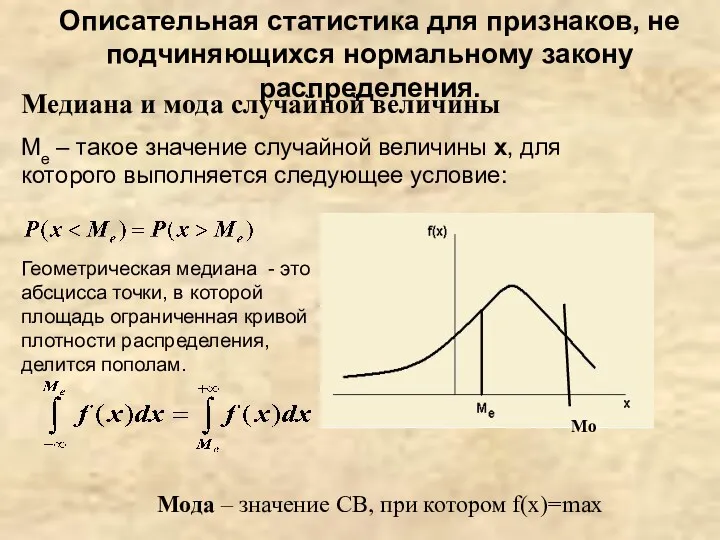
- 5. Описательная статистика для признаков, не подчиняющихся нормальному закону распределения. Медиана и мода случайной величины Me –
- 6. Для характеристики структуры совокупности используются квантили. Квантили характеризуют варианты значений признака, занимающие определенное место в ранжированной
- 7. Рассмотрим способы определения медианы при различных значениях N. Для нахождения медианы измерения записывают в ряд по
- 8. Мода (Мо) Мода (англ. mode) представляет собой наиболее часто встречающееся значение переменной (иными словами, наиболее «модное»
- 9. Квартили представляют собой значения, которые делят две половины выборки (разбитые медианой) еще раз пополам (от слова
- 10. Межквартильный размах Пример: Ме=(7+8)/2=7,5 Q1=(2+4)/2=3 Q3=(9+10)/2=9,5
- 11. Квинтили-это значения признака в упорядоченной по возрастанию совокупности, которые делят совокупность на пять равных частей. Ниже
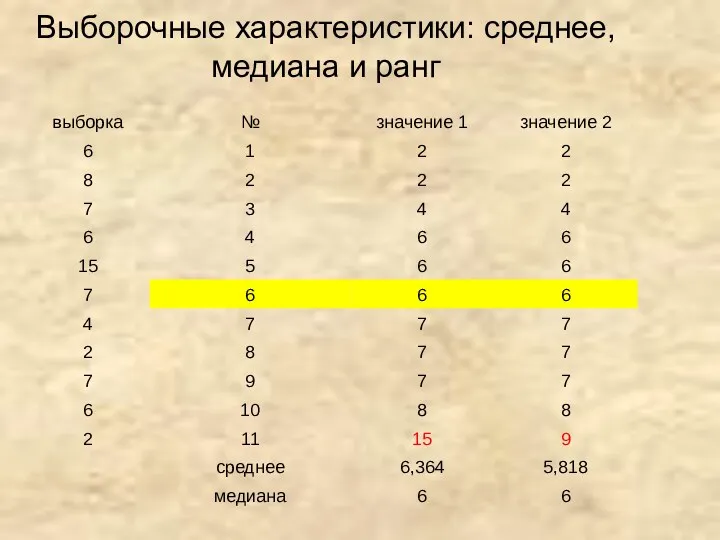
- 12. Выборочные характеристики: среднее, медиана и ранг
- 13. Ранг-место варианты в упорядоченном ряду.
- 14. Основные задачи непараметрической статистики Любое распределение можно охарактеризовать параметром положения, характеризующим центр группирования случайных величин, и
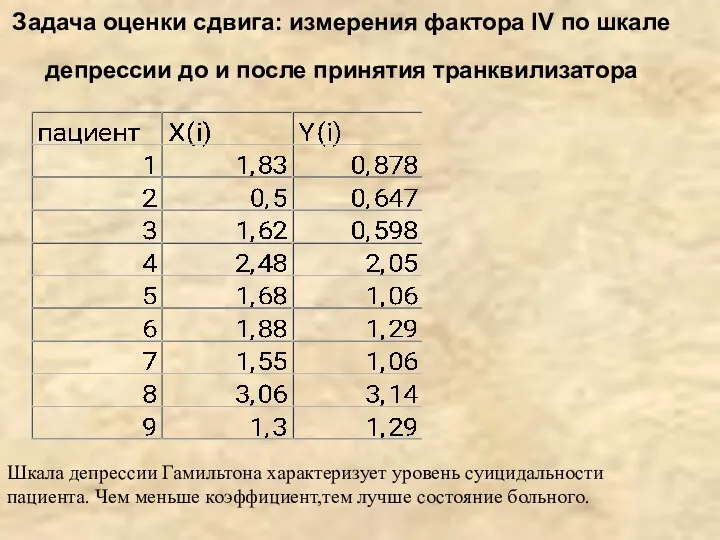
- 15. Задача оценки сдвига: измерения фактора IV по шкале депрессии до и после принятия транквилизатора Шкала депрессии
- 16. Критерий знаков Статистическая модель: разность Z(i) является случайно выбранным наблюдением. Совокупности Z(i) имеют одну и ту
- 17. Биномиальное распределение как основа статистики критерия знаков Если курс лечения не приводит к изменениям, то характеристики
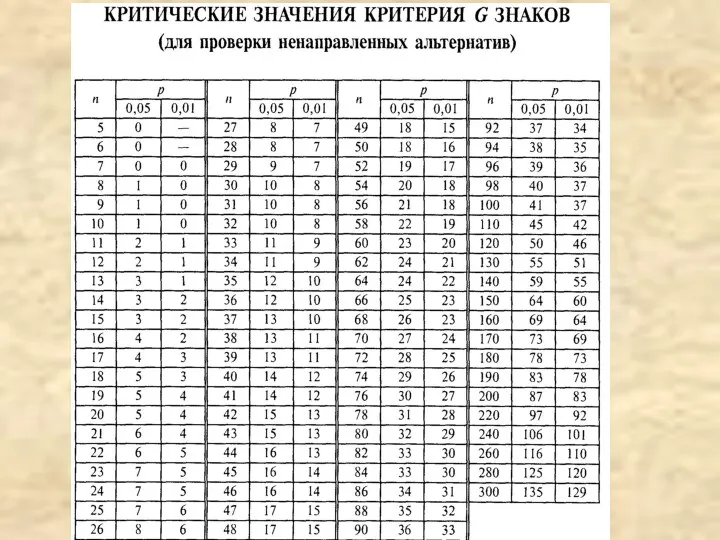
- 18. Критерий знаков N(+)=2; N(-)=7; Gэмп =min(2, 7)=2; Gкрит (0,05,7)=0 Gэмп> Gкрит (2>0) Нулевая гипотеза не отвергается.
- 20. Критерий Уилкоксона для парных выборочных наблюдений (зависимые выборки) Для того, чтобы проверить нулевую гипотезу, нужно: Вычислить
- 21. За эмпирическое значение критерия Тэмп принять наименьшее значение (Т+ или Т-). Определить табличное значение Ткрит для
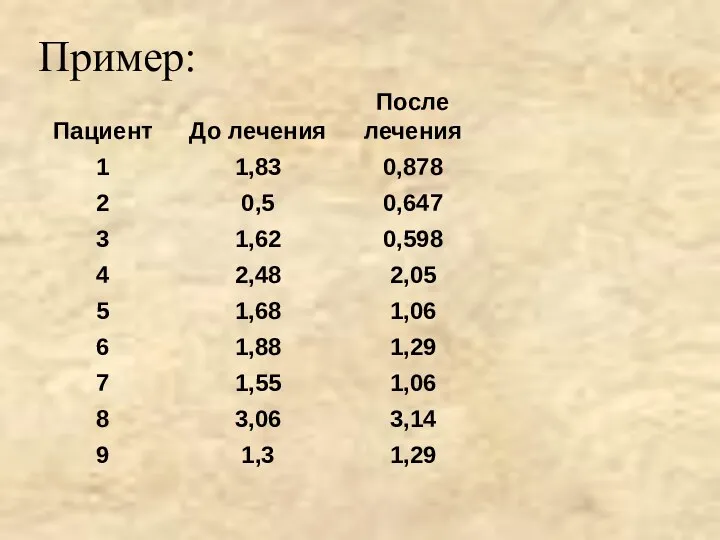
- 22. Пример:
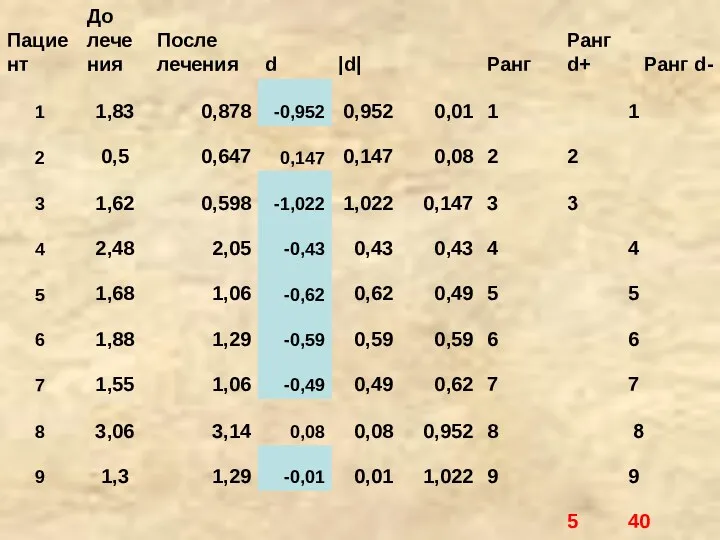
- 24. Общая сумма рангов = 45; Т+ = 5; T- = 40. Т = min(T+, T-) =
- 25. Сравнение двух независимых выборок. Критерий Манна-Уитни Эмпирическое значение критерия Манна-Уитни U показывает насколько совпадают (пересекаются) два
- 26. Находится минимальное значение критерия U=min (U1, U2) а) для малых n: Величина U сравнивается с табличным
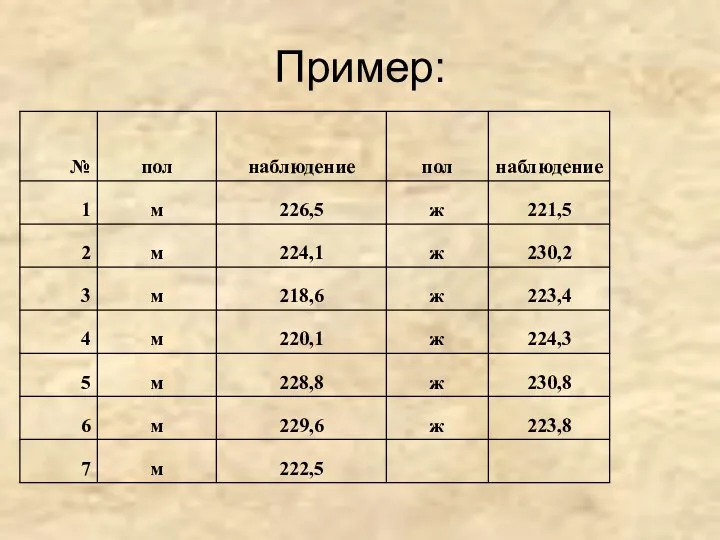
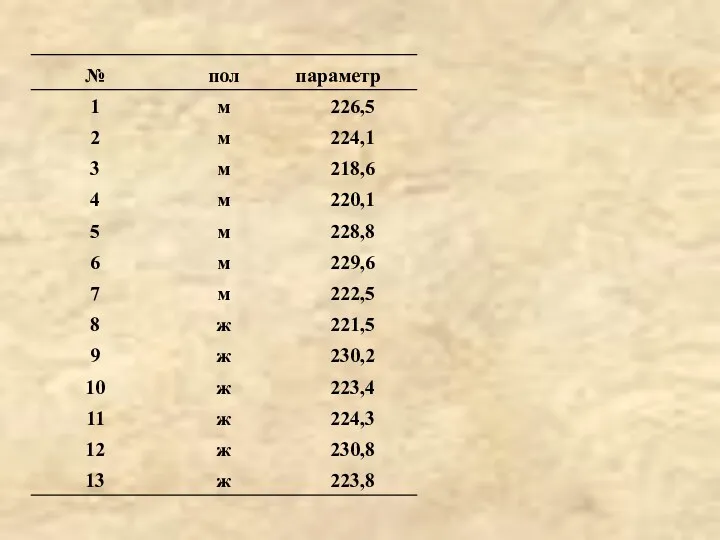
- 27. Пример:
- 29. параметр пол ранг ранг(м) ранг(ж) 218,6 м 1 1 220,1 м 2 2 221,5 ж 3
- 30. Критерий Манна-Уитни n1 =7; n2=6; R1=44; R2= 47; U1=26; U2=16; U1+U2=n1⋅n2 U=min (26,16)=16; Uкр(7,6)=6; U> Uкр
- 31. б) для больших n: применяется критерий z для нормального закона распределения
- 32. Заключение Нами рассмотрены: Описательная статистика для признаков, не подчиняющихся нормальному закону распределения. Непараметрические критерии достоверности различия
- 33. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА: Основная литература: Наследов А.Д. Математические методы психологического исследования – СПб.: Речь, 2008. – 392
- 35. Скачать презентацию























 Формирование познавательного интереса к учению как способ развития креативных способностей личности
Формирование познавательного интереса к учению как способ развития креативных способностей личности Тренинговая работа №4
Тренинговая работа №4 Построение сечений
Построение сечений Возможности программ динамической геометрии в проведении учебного исследования и проекта по математике
Возможности программ динамической геометрии в проведении учебного исследования и проекта по математике Приём сложения однозначных чисел с переходом через десяток
Приём сложения однозначных чисел с переходом через десяток Задачи второго вида на проценты
Задачи второго вида на проценты Четырехугольники: прямоугольник, ромб, квадрат
Четырехугольники: прямоугольник, ромб, квадрат Математический конкурс-викторина
Математический конкурс-викторина Конспект урока по математике в 1 классе УМК Гармония
Конспект урока по математике в 1 классе УМК Гармония Складання задач різних типів за одним сюжетом. Вимірювання довжини відрізка і побудова відрізка заданої довжини (урок № 77)
Складання задач різних типів за одним сюжетом. Вимірювання довжини відрізка і побудова відрізка заданої довжини (урок № 77) Презентация Танграм Люди
Презентация Танграм Люди Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Мінімальний переріз. Основні відомості
Мінімальний переріз. Основні відомості Решение задач на проценты
Решение задач на проценты Конспект урока математики в 3 классе по системе Л.Занкова по теме: Числовой луч
Конспект урока математики в 3 классе по системе Л.Занкова по теме: Числовой луч Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Пифагор и его теорема
Пифагор и его теорема Пентамино
Пентамино Числа и цифры 6,7.
Числа и цифры 6,7. Устный счет 2 класс(первые уроки)
Устный счет 2 класс(первые уроки) Разложение многочлена на множители способом группировки
Разложение многочлена на множители способом группировки Математические олимпийские игры
Математические олимпийские игры Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Образовательная система Школа 2100 Урок матемтики в 1 классе по теме Объём.Литр.
Образовательная система Школа 2100 Урок матемтики в 1 классе по теме Объём.Литр. Окружность. Круг
Окружность. Круг презентация развитие пространственного мышления
презентация развитие пространственного мышления Урок математики по теме Площадь 3 класс
Урок математики по теме Площадь 3 класс Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена