Содержание
- 2. Пусть A=(aij) – квадратная матрица порядка n. Построим произведения по следующему правилу: из каждой строки и
- 3. Вычисление определителя Определитель второго порядка. Определитель третьего порядка равен алгебраической сумме шести произведений. а) правило треугольников
- 4. Свойства определителей 1) При транспонировании матрицы ее определитель не меняется. |A| = |AТ| 2) При перестановке
- 6. 6) Определитель не изменится, если к каждому элементу i-й строки (столбца) прибавить соответствующий элемент k-й строки
- 7. Теорема Лапласа и ее следствие Пусть A = (aij) – матрица размера m×n. Выберем в A
- 8. Пусть A = (aij) – квадратная матрица порядка n. Выберем в A минор первого порядка Mk
- 10. Скачать презентацию







 Построение графика квадратичной функции
Построение графика квадратичной функции Презентация Сложение и вычитание в картинках 1 класс УМК Перспективная начальная школа
Презентация Сложение и вычитание в картинках 1 класс УМК Перспективная начальная школа Занимательная топология
Занимательная топология В гости к Бабе Яге Счёт до 10
В гости к Бабе Яге Счёт до 10 Геометрия Лобачевского
Геометрия Лобачевского Математическая раскраска Колобок
Математическая раскраска Колобок Подготовка к введению задач в 2 действия
Подготовка к введению задач в 2 действия Векторы плоскости. Координаты вектора
Векторы плоскости. Координаты вектора Знаходження невідомого зменшуваного
Знаходження невідомого зменшуваного Вписанные и описанные тела
Вписанные и описанные тела Вероятность и статистика. Операции над множествами: объединение, пересечение, дополнение
Вероятность и статистика. Операции над множествами: объединение, пересечение, дополнение Нормальные алгоритмы Маркова
Нормальные алгоритмы Маркова Гипотезы, переменные, валидность, данные. Введение в статистику, лекция 1
Гипотезы, переменные, валидность, данные. Введение в статистику, лекция 1 Функции нескольких переменных
Функции нескольких переменных Применение свойств квадратного корня
Применение свойств квадратного корня Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Модели для оптимизации порядка формирования и распечатки выходных документов
Модели для оптимизации порядка формирования и распечатки выходных документов Цилиндр
Цилиндр Умножение и деление на 10
Умножение и деление на 10 Степень и ее свойства. 7 класс
Степень и ее свойства. 7 класс Запись, сравнение, сложение и вычитание, округление десятичных дробей
Запись, сравнение, сложение и вычитание, округление десятичных дробей Линейное уравнение с одной переменной. Урок 10
Линейное уравнение с одной переменной. Урок 10 Понятие корня n-й степени из действительного числа
Понятие корня n-й степени из действительного числа Готовимся к ЕГЭ. Математика
Готовимся к ЕГЭ. Математика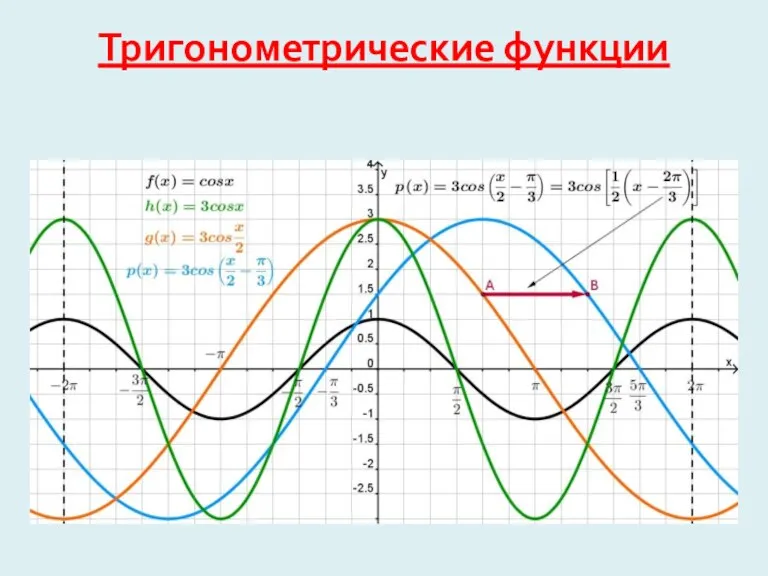 Тригонометрические функции
Тригонометрические функции Курсы для школьников Интересно о сложном. Любопытная математика
Курсы для школьников Интересно о сложном. Любопытная математика Презентация к уроку математики во 2 классе Умножение круглых чисел
Презентация к уроку математики во 2 классе Умножение круглых чисел Транспортна задача лінійного програмування
Транспортна задача лінійного програмування