Содержание
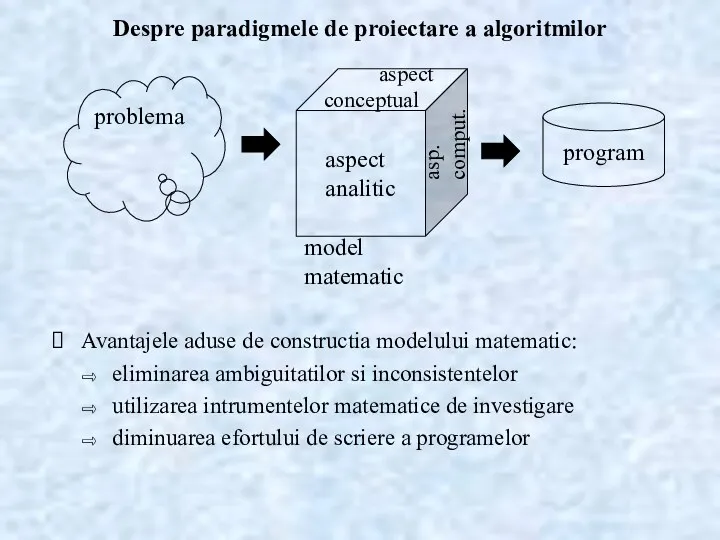
- 2. Despre paradigmele de proiectare a algoritmilor Avantajele aduse de constructia modelului matematic: eliminarea ambiguitatilor si inconsistentelor
- 3. Paradigma divide-et-impera Modelul matematic P(n): problema de dimensiune n baza daca n ≤ n0 atunci rezolva
- 4. Paradigma divide-et-impera: algoritm procedure DivideEtImpera(P, n, S) begin if (n then determina S prin metode elementare
- 5. Paradigma divide-et-impera: complexitate presupunem ca divizarea + asamblarea necesita timpul O(nk) Demonstratia pe tabla
- 6. Cautare binara generalizare: s[p..q] baza: p ≥ q divide-et-impera divide: m = [(p + q)/2] subprobleme:
- 7. Constructia arborelui binar problema intrare: o lista ordonata crescator s = (x0 iesire: arbore binar de
- 8. Sortare prin interclasare (Merge sort) generalizare: a[p..q] baza: p ≥ q divide-et-impera divide: m = [(p
- 9. Sortare rapida (Quick sort) generalizare: a[p..q] baza: p ≥ q divide-et-impera divide: determina k intre p
- 10. Quick sort: partitionare initial: x ← a[p] (se poate alege x arbitrar din a[p..q]) i ←
- 11. Quick sort: complexitate complexitatea in cazul cel mai nefavorabil: T(n) = O(n2) complexitatea medie Teorema
- 12. Selectionare problema intrare: o lista a = (x0, x1, ..., xn-1) iesire: cel de-al k+1-lea numar
- 13. Transformata Fourier discreta I descrierea unui semnal domeniul timp: f(t) domeniul frecventa: F(ν) Transformata Fourier directa:
- 14. Transformata Fourier discreta - aplicatie Filtrarea imaginilor transformata Fourier a unei functii este echivalenta cu reprezentarea
- 15. Transformata Fourier discreta II cazul discret xk = f(tk) k=0,…,n-1 tk = kT, T = perioada
- 16. Transformata Fourier discreta III rolul radacinilor unitatii de ordinul n radacina de ordinul n a unitatii
- 17. Transformata Fourier discreta IV calculul valorilor prin divide-et-impera a = b = 2, k = 1
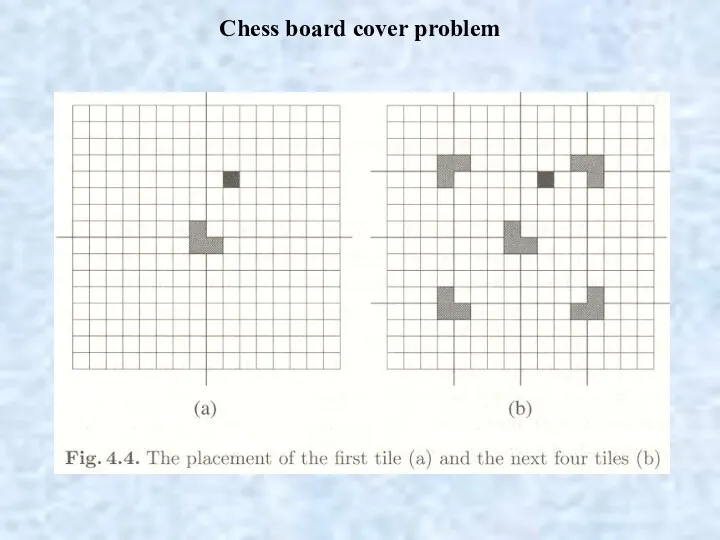
- 18. Chess board cover problem There is a chess board with a dimension of 2m (i.e., it
- 19. Chess board cover problem
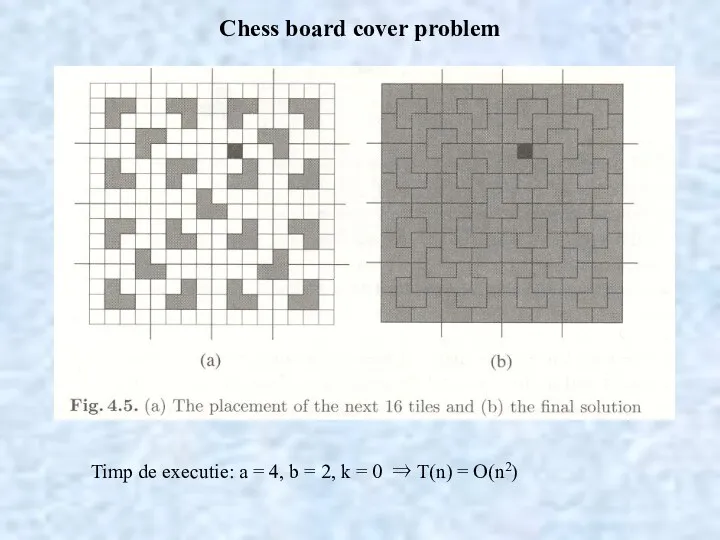
- 20. Chess board cover problem Timp de executie: a = 4, b = 2, k = 0
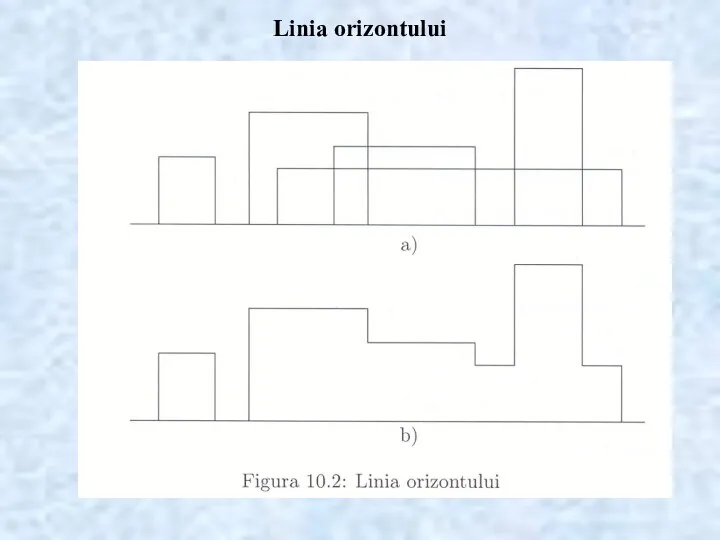
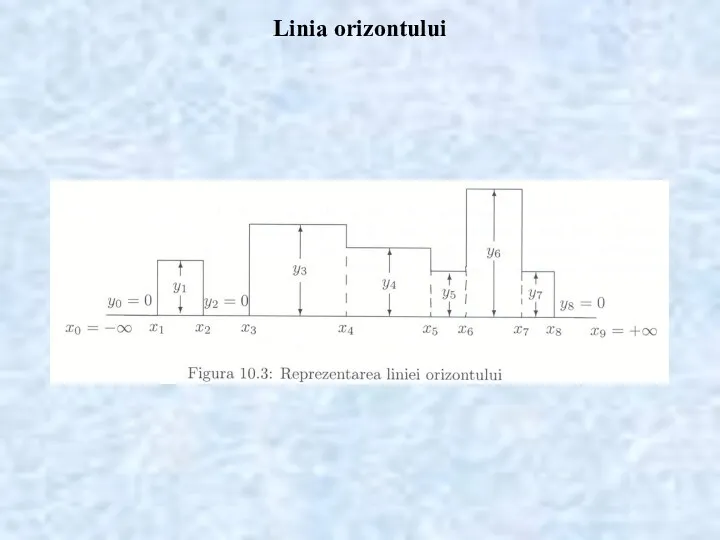
- 21. Linia orizontului
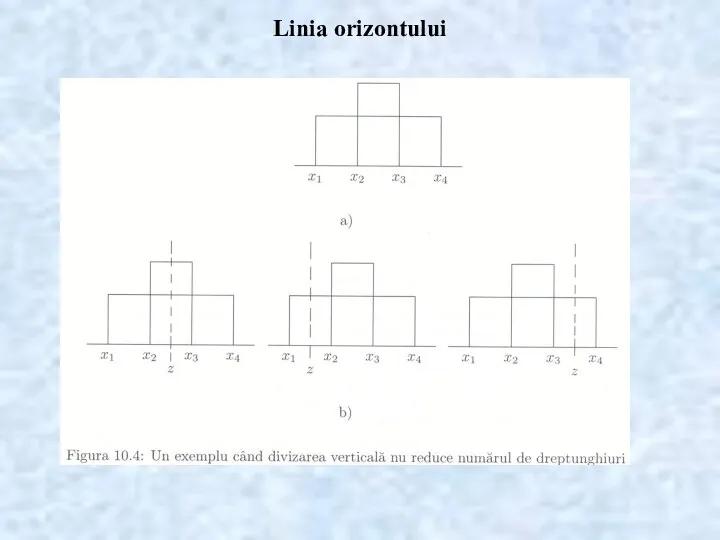
- 22. Linia orizontului
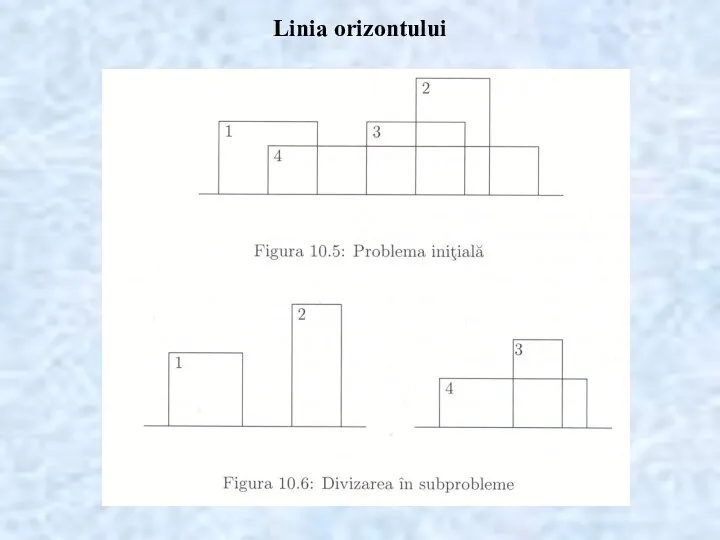
- 23. Linia orizontului
- 24. Linia orizontului
- 26. Скачать презентацию



![Cautare binara generalizare: s[p..q] baza: p ≥ q divide-et-impera divide:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/377186/slide-5.jpg)

![Sortare prin interclasare (Merge sort) generalizare: a[p..q] baza: p ≥](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/377186/slide-7.jpg)
![Sortare rapida (Quick sort) generalizare: a[p..q] baza: p ≥ q](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/377186/slide-8.jpg)
![Quick sort: partitionare initial: x ← a[p] (se poate alege](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/377186/slide-9.jpg)








 Векторная алгебра (лекция 11)
Векторная алгебра (лекция 11) Линейные пространства. Нормированные пространства. Подпространства
Линейные пространства. Нормированные пространства. Подпространства Квадрат теңдеу және оның түбірлері
Квадрат теңдеу және оның түбірлері Нестандартные способы решения квадратных уравнений
Нестандартные способы решения квадратных уравнений Понятие призмы
Понятие призмы Неопределённость в измерениях
Неопределённость в измерениях презентация к занятию по ФЭМП для средней группы
презентация к занятию по ФЭМП для средней группы Тренажёр. Примеры в пределах 20. (1 класс)
Тренажёр. Примеры в пределах 20. (1 класс) Измерение углов
Измерение углов Логика предикатов
Логика предикатов Параллельные прямые. Школа доказательства
Параллельные прямые. Школа доказательства Последовательность. Лингво–математический урок
Последовательность. Лингво–математический урок Музична таблиця множення
Музична таблиця множення Решение задач по сумме и разности. Презентация.
Решение задач по сумме и разности. Презентация. Рациональные числа и действия над ними. 6 класс
Рациональные числа и действия над ними. 6 класс Безотметочное обучение в начальной школе
Безотметочное обучение в начальной школе Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Аксиома параллельных прямых. Доказательство от противного
Аксиома параллельных прямых. Доказательство от противного Сonstructive problems and optimization
Сonstructive problems and optimization Приемы смыслового чтения при решении текстовых задач по математике
Приемы смыслового чтения при решении текстовых задач по математике Задачи на смекалку
Задачи на смекалку Окружность, хорда, диаметр
Окружность, хорда, диаметр Математика. 1 класс. Урок 16. Отрезок. Презентация
Математика. 1 класс. Урок 16. Отрезок. Презентация Применение производной к решению задач
Применение производной к решению задач Нумерация
Нумерация Презентация к уроку математики (Школа 2100 3 класс)
Презентация к уроку математики (Школа 2100 3 класс) Решение заданий В8 (часть 2) по материалам открытого банка задач ЕГЭ по математике
Решение заданий В8 (часть 2) по материалам открытого банка задач ЕГЭ по математике Счет предметов, математика, 1 класс
Счет предметов, математика, 1 класс