Слайд 2
Обозначения
Заглавные латинские буквы (A, …)- множества
Прописные латинские буквы (a,b…) – элементы множества

Слайд 3
Поле
Определение. Множество К называется полем, если в нем введены две бинарные операции: сложение
и умножение
удовлетворяющие аксиомам:

Слайд 4

Слайд 5

Слайд 6
Простейшие свойства поля
Нулевой элемент единственный
Противоположный элемент единственный.
Единичный элемент единственный.
Обратный элемент единственный.

Слайд 7
Определение вычитания и деления в поле
Определение.
Замечание. Такое определение корректно, благодаря единственности противоположного и
обратного элемента.

Слайд 8
Примеры полей
Множество R – вещественных чисел является полем
Множество Q - рациональных чисел является
полем.
Множество F2 ={0,1} – из двух элементов является полем

Слайд 9
Линейное пространство.
Определение. Множество V называется линейным пространством над полем K, если в нем
введены две бинарные операции: сложение и умножение на число из поля
удовлетворяющие аксиомам:

Слайд 10

Слайд 11

Слайд 12
Простейшие следствия из аксиом ЛП
Нулевой элемент единственный.
Противоположный вектор единственный.
Определение:

Слайд 13
Линейная комбинация векторов
V- ЛП
Определение. Выражение вида
называется линейной комбинацией векторов

Слайд 14
Линейная оболочка векторов
Определение. Пусть - система векторов. Множество всех линейных комбинаций данной системы
векторов называют линейной оболочкой системы векторов:

Слайд 15
Выражение вектора через линейную комбинацию
Определение. Если некоторый вектор
представлен в виде
то говорят,
что вектор линейно выражается через вектора

Слайд 16
Линейная зависимость
Определение. Система векторов называется
линейно зависимой, если существует ненулевой набор
чисел
таких, что

Слайд 17
Линейная независимость
Определение. Система векторов
называется линейно независимой, если
тогда и только тогда,
когда все числа
равны нулю.

Слайд 18
Алгебраические свойства систем линейных векторов.
Если система векторов содержит нулевой вектор, то она линейно
зависима.
Если часть системы векторов (подсистема) линейно зависима, то и вся система векторов тоже линейно зависима.
Система векторов линейно зависима тогда и только тогда, когда существует вектор, линейно выражающийся через остальные вектора

Слайд 19
Геометрические свойства систем векторов.
Система состоящая из одного вектора линейно зависима тогда и только
тогда, когда этот вектор нулевой.
Система состоящая из двух векторов линейно зависима тогда и только тогда, когда вектора коллинеарны.
Система состоящая из трех векторов линейно зависима тогда и только тогда, когда три вектора компланарны.

Слайд 20
Базис линейного пространства
V – ЛП
Определение. Система векторов
называется базисом ЛП V,
если эта
система ЛНЗ и любой вектор из V линейно выражается через
Замечание. В ЛП V базис определяется не единственным образом (можно выбрать несколько базисов), но количество базисных векторов n остается неизменной величиной.

Слайд 21
Размерность линейного пространства
Определение. Количество векторов в базисе называется размерностью линейного пространства V.
Обозначение. dimV=n.

Слайд 22
Координаты вектора в базисе
Из определения базиса ЛП V следует, что любой вектор в
этом ЛП линейно выражается через базисные векторы :
Определение. Координатами вектора x называются коэффициенты в разложении по базисным векторам:

Слайд 23
Координаты вектора в базисе
Замечание. Координаты вектора x зависят от выбора базиса. В разных
базисах у одного и того же вектора x разные координаты.

Слайд 24
Подпространства линейного пространства

Слайд 25
Подпространства и подмножества
Определение. Подмножество W линейного пространства V называется линейным подпространством, если оно
является линейным пространством относительно операций из V.
Обозначение.
Утверждение. (ноль принадлежит любому подпространству)
Утверждение. Для любого линейного пространства V подмножества {0} и V являются подпространствами.

Слайд 26

Слайд 27
Равносильное определение.
Утверждение. Множество W является линейным подпространством V тогда и только тогда, когда
оно замкнуто относительно операций сложения и умножения на число:

Слайд 28
Подпространства матриц
Пусть
W1 – симметрические матрицы
W2 – кососимметрические матрицы

Слайд 29
Подпространства C[a,b]
Пусть V=C[a,b] – пространство непрерывных функций на отрезке [a,b]
![Подпространства C[a,b] Пусть V=C[a,b] – пространство непрерывных функций на отрезке [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/337909/slide-28.jpg)
Слайд 30
Пересечение и объединение подпространств
Пусть V – ЛП, W1, W2 – подпространства V
Определение.
Утверждение. Пересечение
подпространств
является подпространством.
Замечание. Объединение подпространств
не является подпространством.

Слайд 31
Сумма подпространств
Определение.
Утверждение. Сумма двух подпространств является подпространством.
Замечание. Разложение произвольного вектора из W1+W2 по
W1 и W2 возможно не единственным образом.

Слайд 32
Пример суммы подпространств
Пример. W1=XOY
W2=YOZ
W1+W2=R3
Поскольку для любого вектора возможно разложение:

Слайд 33
Прямая сумма подпространств
Определение. Пространство V называется прямой суммой подпространств W1 и W2, если
V=W1+W2 и любой вектор x представим в виде x=w1+w2 единственным образом.
Обозначение.
Пример.
Поскольку разложение единственнно

Слайд 34
Теорема о размерности
Теорема. Пусть V=W1+W2. Тогда
Доказательство.
Пусть e1, e2….ek - базис W1∩W2 .
dim(W1∩W2
)=k
e1, e2….ek, a1, a2…. aℓ - базис W1, dimW1=k+ℓ
e1, e2….ek, b1, b2…. bm - базис W2, dimW2=k+m
Для доказательства теоремы достаточно проверить, что e1, e2….ek, a1, a2…. aℓ b1, b2…. bm - базис V

Слайд 35
Доказательство
Проверим, что e1, e2….ek, a1, a2…. aℓ b1, b2…. bm ЛНЗ система векторов
Левая
часть последнего равенства принадлежит W1, правая часть принадлежит W2, следовательно и левая и правая части принадлежат W1∩W2, это значит, что правую часть можно выразить через базис пересечения.

Слайд 36

Слайд 37

Слайд 38
Доказательство
2. Проверим, что любой вектор из ЛП V линейно выражается через систему e1,…ek,
a1,…aℓ, b1…bm.
□

Слайд 39
Теоремы о прямой сумме
Теорема 1. Пусть V=W1+W2. Тогда
Тогда и только тогда, когда ноль
раскладывается единственным образом:
.
Теорема 2.

Слайд 40
Изменение координат вектора при замене базиса

Слайд 41
Матрица перехода
V – линейное пространство
e1, e2,e3…..en – первый базис (1)
e’1, e’2,e’3,…e’n – второй
базис (2)
(количество векторов n=dimV, но сами вектора разные)
Выразим вектора второго базиса через вектора первого базиса:

Слайд 42

Слайд 43

Слайд 44

Слайд 45
Изменение координат вектора

Слайд 46

Слайд 47

Слайд 48
Изоморфизм линейных пространств

Слайд 49
Определение изоморфизма
V1, V2 – два ЛП
Определение. Пространство V1 изоморфно V2, если существует взаимно-однозначное
соответствие f: V1→V2 такое, что f(x1+x2)=f(x1)+f(x2) и f(αx1)=αf(x1) для любых x1, x2 принадлежащих V1, α принадлежащих K.
Обозначение.

Слайд 50
Свойства изоморфизма
Рефлективность
Симметричность
Транзитивность

Слайд 51
Утверждение. Если V1 изоморфно V2, то f(0v1)=0v2 (при изоморфизме ноль переходит в ноль)
Доказательство.

Слайд 52
Теорема. V изоморфно W тогда и только тогда, когда dimV=dimW.
Доказательство.

Слайд 53
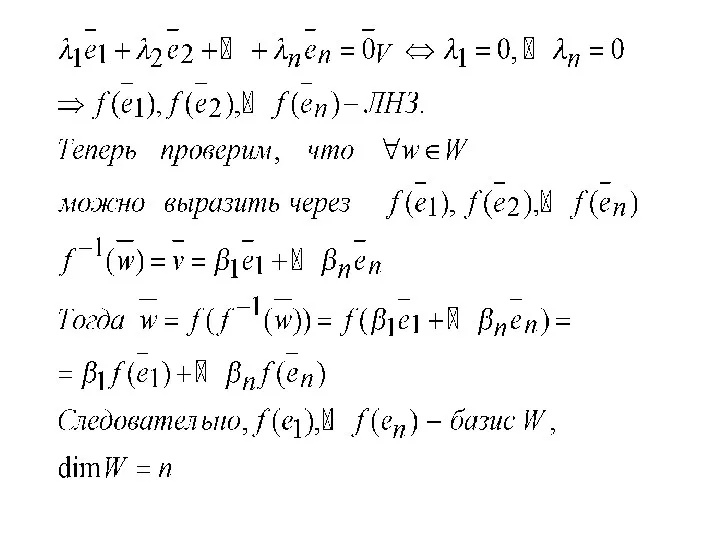
Слайд 54

Слайд 55
Утверждение. Любое линейное пространство размерности n изоморфно n-мерному координатному пространству Rn.
Доказательство.
Всякий вектор v=α1e1+…αnen
принадлежащий ЛП V изоморфен вектору с координатами (α1,….αn)
(Выполнение свойств изоморфизма проверить самостоятельно)




























![Подпространства C[a,b] Пусть V=C[a,b] – пространство непрерывных функций на отрезке [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/337909/slide-28.jpg)

























 Приближенные числа. Учет погрешностей результатов операций над приближенными числами
Приближенные числа. Учет погрешностей результатов операций над приближенными числами Эксперттік бағалау әдістері
Эксперттік бағалау әдістері Единицы измерения
Единицы измерения Свойства функций. Кусочно-заданные функции
Свойства функций. Кусочно-заданные функции Золотое сечение, или Божественная пропорция
Золотое сечение, или Божественная пропорция Арифметическая прогрессия
Арифметическая прогрессия Презентация Устный счёт Диск
Презентация Устный счёт Диск Деление обыкновенных дробей. 6 класс
Деление обыкновенных дробей. 6 класс Умножение на двузначное число. Площадь прямоугольника
Умножение на двузначное число. Площадь прямоугольника Презентация к уроку Состав числа 7
Презентация к уроку Состав числа 7 Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Сложение отрицательных чисел
Сложение отрицательных чисел Предмет, метод и задачи статистики
Предмет, метод и задачи статистики Формирование интереса к математике у детей старшего дошкольного возраста
Формирование интереса к математике у детей старшего дошкольного возраста Разрезание и складывание фигур
Разрезание и складывание фигур Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы
Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы Решение нестандартных задач при подготовке к ЕГЭ
Решение нестандартных задач при подготовке к ЕГЭ Урок 39. Сумма и произведение. Знак умножения.
Урок 39. Сумма и произведение. Знак умножения. Своя игра по математике
Своя игра по математике Прямоугольный параллелепипед
Прямоугольный параллелепипед Таблица умножения и деления на 6
Таблица умножения и деления на 6 Методы решения системы трёх линейных уравнений с тремя неизвестными
Методы решения системы трёх линейных уравнений с тремя неизвестными Свойства множеств
Свойства множеств Десятичная запись дробных чисел
Десятичная запись дробных чисел Определение числовой функции и способы её задания
Определение числовой функции и способы её задания История создания страны формул
История создания страны формул устный счет
устный счет Движения. Центральная симметрия
Движения. Центральная симметрия