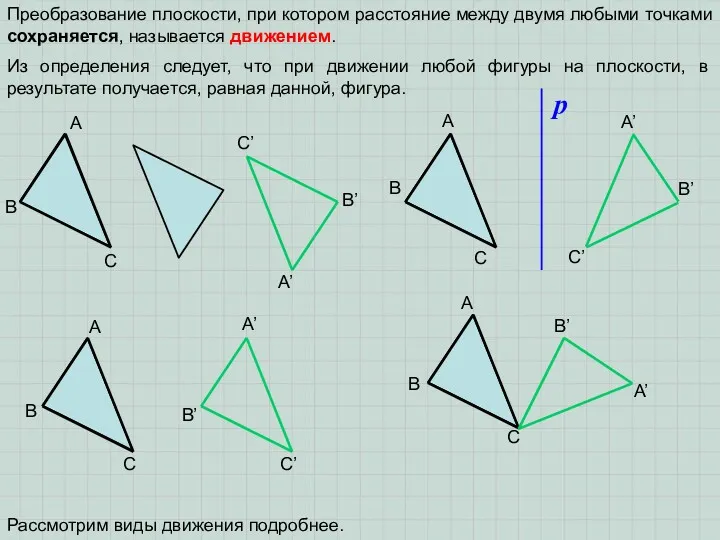
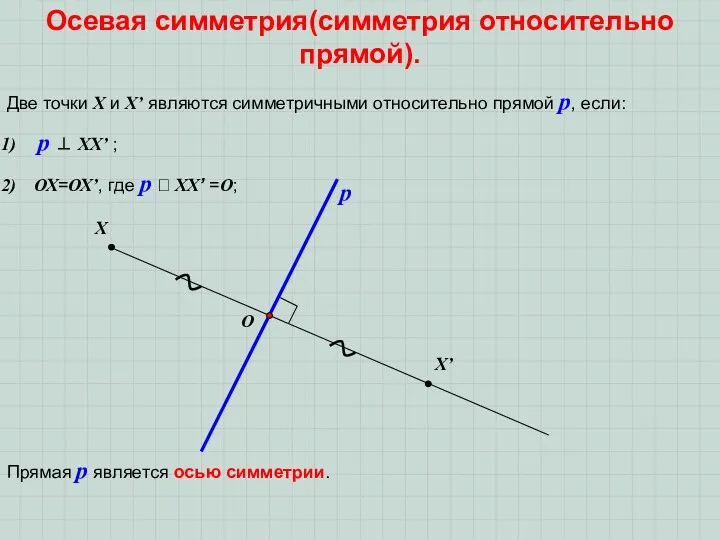
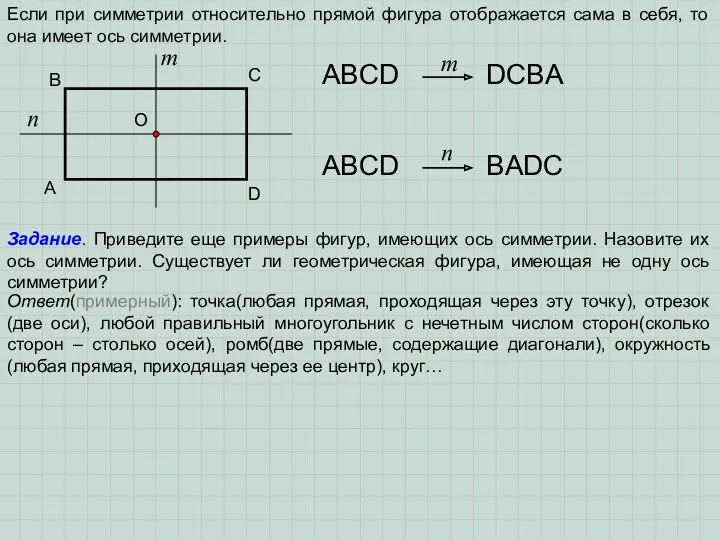
Если при симметрии относительно прямой фигура отображается сама в себя, то
она имеет ось симметрии.
A
B
C
D
O
ABCD
DСBA
m
Задание. Приведите еще примеры фигур, имеющих ось симметрии. Назовите их ось симметрии. Существует ли геометрическая фигура, имеющая не одну ось симметрии?
Ответ(примерный): точка(любая прямая, проходящая через эту точку), отрезок(две оси), любой правильный многоугольник с нечетным числом сторон(сколько сторон – столько осей), ромб(две прямые, содержащие диагонали), окружность(любая прямая, приходящая через ее центр), круг…
m
n
ABCD
BADС
n


 Вивчаємо арифметичні дії множення і ділення
Вивчаємо арифметичні дії множення і ділення Игра для учащихся Математический активизатор
Игра для учащихся Математический активизатор Приемы умножения и деления на 10
Приемы умножения и деления на 10 Взаимосвязь между скоростью, временем и расстоянием. Урок математики в 5 классе
Взаимосвязь между скоростью, временем и расстоянием. Урок математики в 5 классе Однозначные числа
Однозначные числа Урок по математике Дециметр 1 класс
Урок по математике Дециметр 1 класс Числовые и буквенные выражения (4 класс)
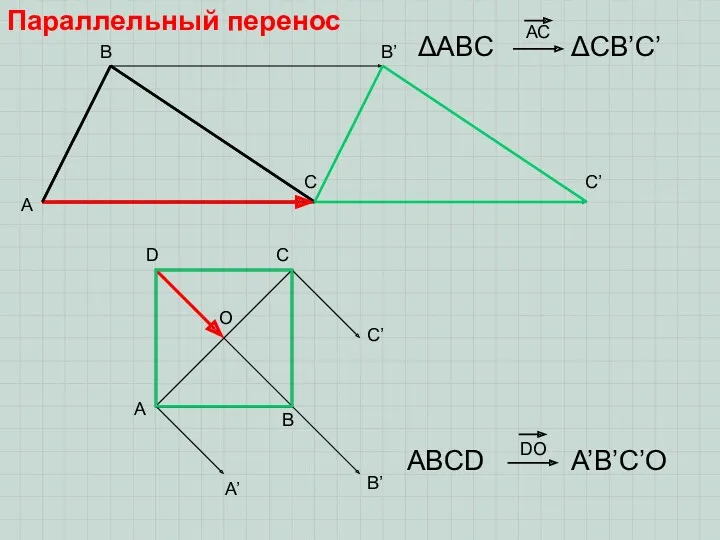
Числовые и буквенные выражения (4 класс) Параллельный перенос и его свойства
Параллельный перенос и его свойства Решение показательных уравнений
Решение показательных уравнений Суть метода Ньютона
Суть метода Ньютона Наименьшее общее кратное
Наименьшее общее кратное Объем конуса
Объем конуса Степенная функция. Ее свойства и графики
Степенная функция. Ее свойства и графики Теорема Пифагора
Теорема Пифагора Презентация к уроку
Презентация к уроку Текстовые задачи ЕГЭ
Текстовые задачи ЕГЭ Математическая логика
Математическая логика Тригонометрические функции произвольного угла
Тригонометрические функции произвольного угла Дискретная математика. Часть 2 Отношения на множествах и элементы комбинаторики
Дискретная математика. Часть 2 Отношения на множествах и элементы комбинаторики Игра-тренажер 1 класс Сложение с переходом через 10
Игра-тренажер 1 класс Сложение с переходом через 10 Возведение в куб суммы и разности двух выражений
Возведение в куб суммы и разности двух выражений Леонард Эйлер. Круги Эйлера
Леонард Эйлер. Круги Эйлера Как и когда люди научились считать и записывать числа?
Как и когда люди научились считать и записывать числа? Таблица умножения и деления на 2. Игра-тренажер
Таблица умножения и деления на 2. Игра-тренажер Построения циркулем и линейкой
Построения циркулем и линейкой Презентация: Периметр многоугольника
Презентация: Периметр многоугольника Многочлен и его стандартный вид
Многочлен и его стандартный вид Ох уж эта математика
Ох уж эта математика