Содержание
- 2. Применение дифференциала для приближенных вычислений. Из определения производной функции: Можно записать: , или . Величина -
- 3. Пример: вычислить без таблицы Sin29 ͦ Sin29 ͦ=Sin(30 ͦ-1 ͦ), поэтому примем x=30 ͦ, а Δx=-1
- 4. Частные производные функций
- 5. Частные и полный дифференциал функции
- 6. Задача: найдите абсолютную погрешность в определении объема цилиндра, если при измерениях были получены радиуса r= (6±0,1)
- 7. Интегральное исчисление. Первообразная функция. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если
- 8. Неопределенный интеграл. Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) +
- 10. Свойства: где u, v, w – некоторые функции от х. Пример:
- 11. Методы интегрирования А) Непосредственное интегрирование.
- 12. Б) Способ подстановки (замены переменных).
- 13. В) Интегрирование по частям.
- 14. Пример. Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному
- 16. Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)
- 17. Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x)
- 18. Свойства определенного интеграла. 4. Если f(x) ≤ ϕ(x) на отрезке [a, b] a
- 19. 5.Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b],
- 20. 8. Для произвольных чисел a, b, c справедливо равенство: Теорема: (Теорема Ньютона – Лейбница) Если функция
- 21. Пример.
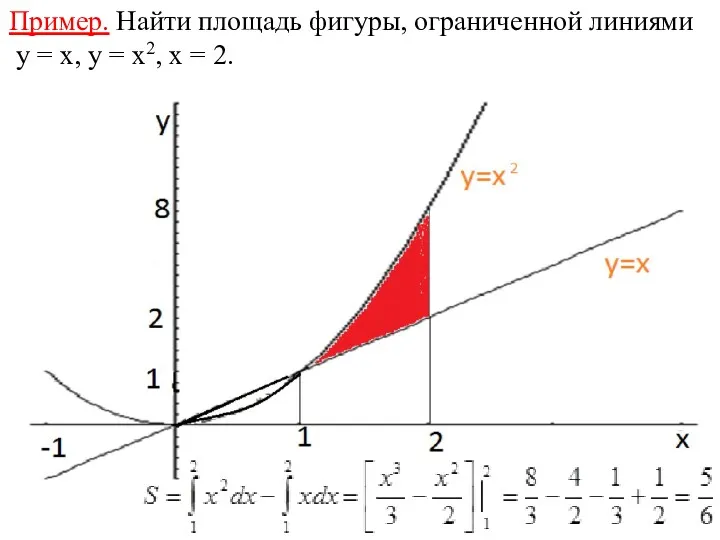
- 22. Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
- 23. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 26. Скачать презентацию







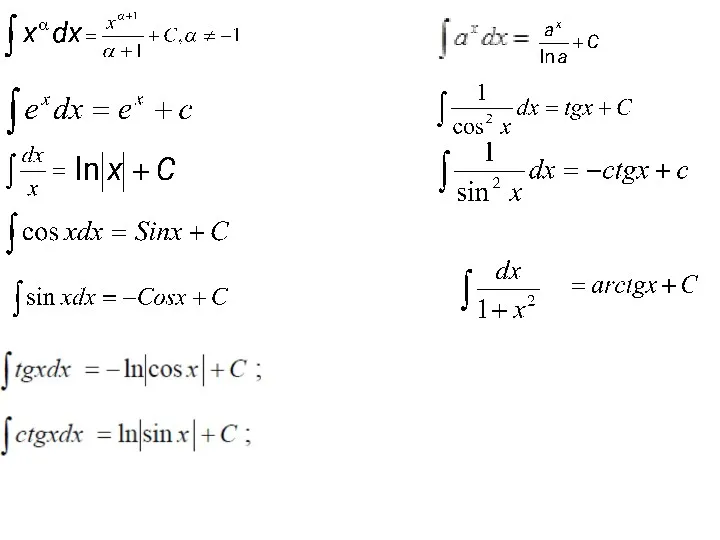





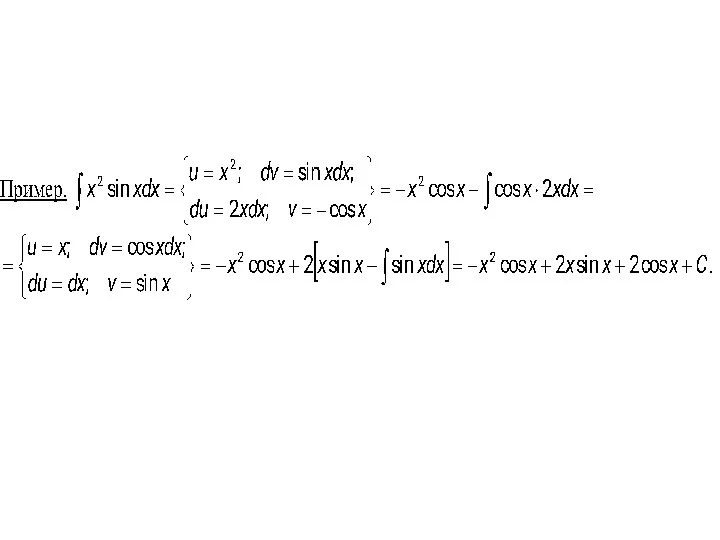
![Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/221878/slide-15.jpg)

![Свойства определенного интеграла. 4. Если f(x) ≤ ϕ(x) на отрезке [a, b] a](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/221878/slide-17.jpg)





 Показательная функция, уравнения, неравенства
Показательная функция, уравнения, неравенства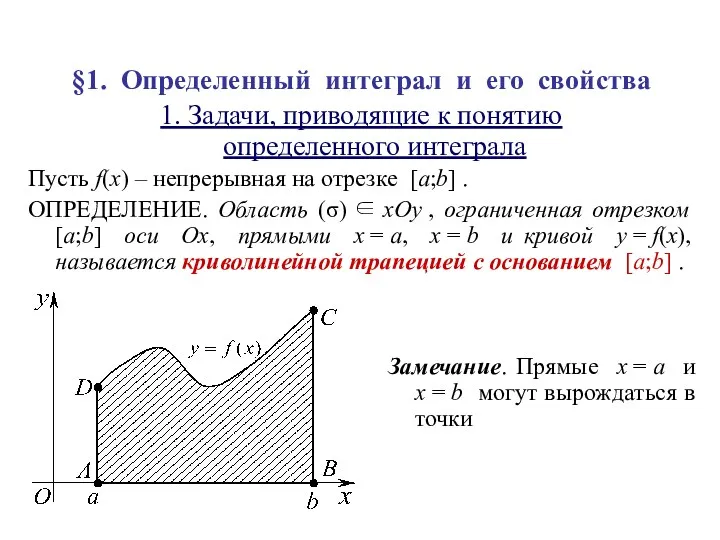 Определенный интеграл и его свойства. Тема 1
Определенный интеграл и его свойства. Тема 1 УМК по предмету Счёт и конструирование и дидактический материал по данной теме, для подготовительного класса
УМК по предмету Счёт и конструирование и дидактический материал по данной теме, для подготовительного класса Многочлены и рациональные функции
Многочлены и рациональные функции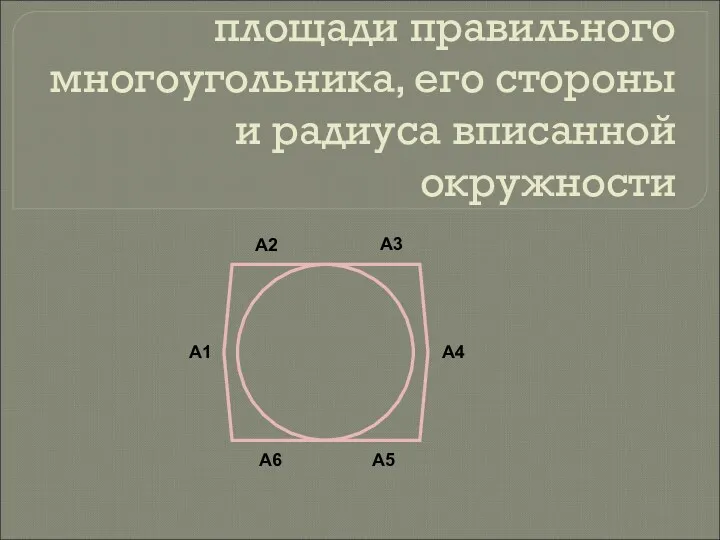 Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Случаи сложения вида + 8, + 9
Случаи сложения вида + 8, + 9 Рациональные числа
Рациональные числа Временные ряды и их применение для анализа и прогнозирования
Временные ряды и их применение для анализа и прогнозирования Презентация Использование оборудования кабинета математики отв. Евдокимова Г.Ю.
Презентация Использование оборудования кабинета математики отв. Евдокимова Г.Ю. Величины.
Величины. ЕГЭ профильная математика. Задание № 4
ЕГЭ профильная математика. Задание № 4 Геометрический смысл производной
Геометрический смысл производной Транспортная задача
Транспортная задача Комбинаторика. Теория вероятности
Комбинаторика. Теория вероятности Решение задач с помощью уравнений
Решение задач с помощью уравнений Коэффициент корреляции рангов Спирмена
Коэффициент корреляции рангов Спирмена Математика 2 сынып. Тәулік. Уақытты анықтаймын
Математика 2 сынып. Тәулік. Уақытты анықтаймын Интеллектуальная игра для обучающихся 4 класса.
Интеллектуальная игра для обучающихся 4 класса. Умножение обыкновенных дробей
Умножение обыкновенных дробей Допустимые значения переменных, входящих в дробное выражение. Урок № 2. 8 класс
Допустимые значения переменных, входящих в дробное выражение. Урок № 2. 8 класс Свойства функции. Алгебра
Свойства функции. Алгебра Решение задач части В (В1, В4)
Решение задач части В (В1, В4) Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Веселый счет
Веселый счет Модуль Геометрия 8 класс
Модуль Геометрия 8 класс Класифікація кутів
Класифікація кутів Дециметр. Предложение
Дециметр. Предложение Банковские задачи. (ЕГЭ. Задание 17)
Банковские задачи. (ЕГЭ. Задание 17)