Содержание
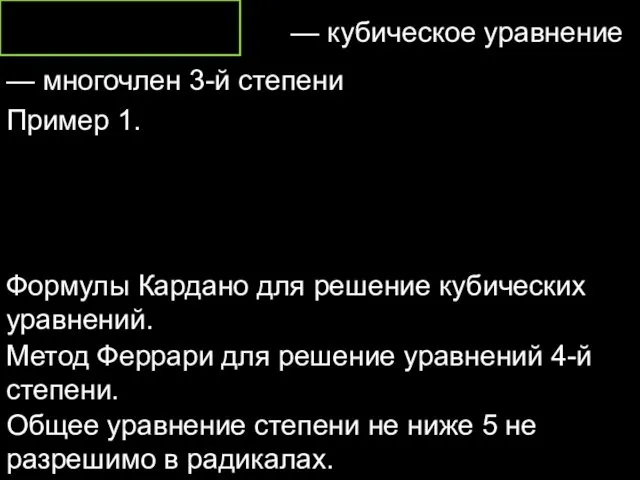
- 2. — кубическое уравнение — многочлен 3-й степени Пример 1. Формулы Кардано для решение кубических уравнений. Метод
- 3. Выражение вида где называется многочленом n-й степени. Обозначается: Число называется корнем многочлена если
- 4. Теорема 1 (о делении с остатком). Пусть — некоторые многочлены; Тогда существуют многочлены такие, что причем
- 5. Пример 2. Найти Решение. Разделим в столбик.
- 6. Значит,
- 7. Теорема 2 (Безу). Остаток от деления многочлена на двучлен равен значению при Пример.
- 8. Доказательство. Пусть — остаток от деления на По теореме 1 степень многочлена меньше степени многочлена т.е.
- 9. Следствие. Число является корнем многочлена тогда и только тогда, когда остаток от деления на равен нулю.
- 10. Таким образом, если известен один из корней уравнения то степень уравнения можно понизить на 1, разделив
- 11. Схема Горнера Деление многочлена на двучлен, удобно выполнять по следующей схеме. Пусть в результате деления многочлена
- 12. Пример. Разделить на 3 1 1 – 6 – 14 – 11 – 3 1 4
- 13. Теорема 3 (основная теоремы алгебры). Всякий многочлен n-й степени ( ) имеет по крайней мере один
- 14. Следствие (основной теоремы алгебры). Всякий многочлен n-й степени ( ) имеет равно n корней (действительных или
- 15. Рациональные корни многочлена Теорема 4. Пусть где Если несократимая дробь является корнем этого многочлена, то p
- 16. Доказательство. По условию теоремы т.е. Тогда (1) (2)
- 17. Правая часть равенства (1) делится на q, значит и левая часть (1) делится на q. Так
- 18. Пример. Решить уравнение Решение. Применим теорему 4: Возможные корни: Проверим с помощью схемы Горнера, какие из
- 19. 1 2 – 3 – 11 6 2 – 1 – 12 — не корень –
- 20. п.2. Рациональные функции. Рациональной функцией называется отношение двух многочленов. ― правильная рациональная дробь; ― неправильная рациональная
- 21. Пример.
- 22. Всякую неправильную рациональную дробь путем деления можно представить в виде суммы многочлена и правильной рациональной дроби.
- 23. Простейшие рациональные дроби I. II. III. IV.
- 24. Теорема 5. Всякую правильную рациональную дробь знаменатель которой разложен на множители можно представить (и притом единственным
- 25. Множителю вида соответствует сумма k простейших дробей Множителю вида соответствует сумма s простейших дробей
- 26. Пример. Разложить в сумму простейших дробей Решение.
- 27. Метод неопределенных коэффициентов Пример. Разложить в сумму простейших дробей Решение.
- 28. Приравняем конечный и исходный числитель, раскрыв скобки: Выпишем слагаемые с Получаем уравнение: Выпишем слагаемые с x:
- 29. Выпишем слагаемые без x: Осталось решить систему: Поэтому,
- 30. Метод отдельных значений аргумента Пример. Разложить в сумму простейших дробей Решение.
- 32. Скачать презентацию



























 Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ
Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ Единицы времени(презентация)
Единицы времени(презентация) Определение высоты здания
Определение высоты здания Сравнение дробей
Сравнение дробей Повторение пройденного
Повторение пройденного Площадь трапеции
Площадь трапеции Третий признак подобия треугольников
Третий признак подобия треугольников Страничка для любознательных. 2 класс
Страничка для любознательных. 2 класс Проверка знаний по математике . 4 класс ( I полугодие)
Проверка знаний по математике . 4 класс ( I полугодие) Векторы. Понятие вектора
Векторы. Понятие вектора Умножение с увлечением! Знакомство с различными способами умножения натуральных чисел. 3 класс
Умножение с увлечением! Знакомство с различными способами умножения натуральных чисел. 3 класс Пересечение и объединение множеств
Пересечение и объединение множеств Презентация к уроку по математике
Презентация к уроку по математике Треугольник. Геометрическая фигура
Треугольник. Геометрическая фигура Теорема о сумме углов треугольника. Задачи
Теорема о сумме углов треугольника. Задачи Найди отличия
Найди отличия Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел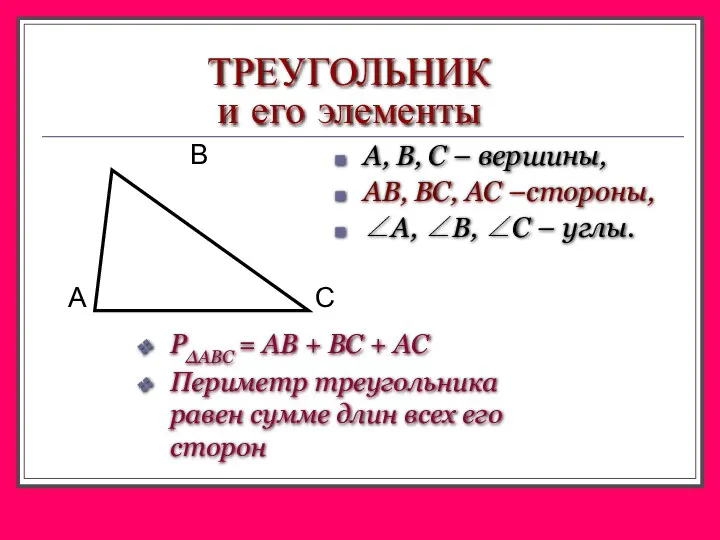 Треугольник и его элементы
Треугольник и его элементы Множества и операции над ними
Множества и операции над ними Ремонт моей комнаты. Математика
Ремонт моей комнаты. Математика Сравнение, сложение, вычитание дробей с разными знаменателями. 6 класс
Сравнение, сложение, вычитание дробей с разными знаменателями. 6 класс Математика. 1 класс. Урок 91. Табличное сложение - Презентация
Математика. 1 класс. Урок 91. Табличное сложение - Презентация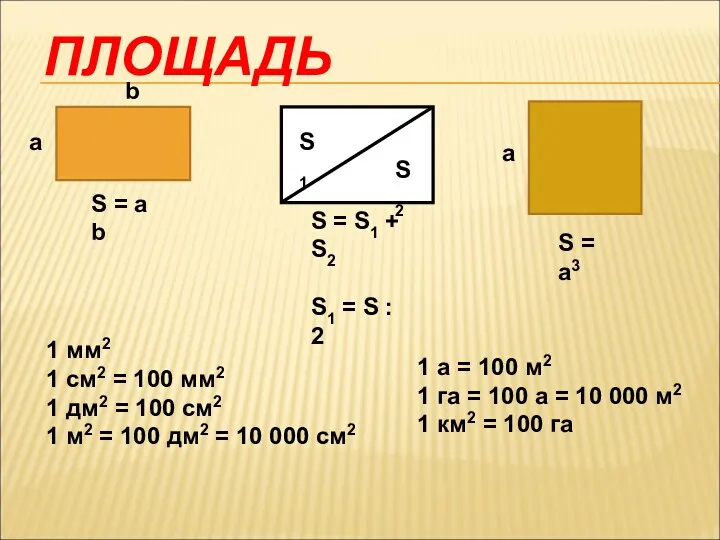 Площадь. Объем
Площадь. Объем Деятельность учителя в условиях реализации ФГОС
Деятельность учителя в условиях реализации ФГОС Защита информации
Защита информации Начальные сведения из стереометрии. Многогранники
Начальные сведения из стереометрии. Многогранники Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Интерактивное пособие математика 1 класс 1 часть Состав числа
Интерактивное пособие математика 1 класс 1 часть Состав числа