Содержание
- 2. Содержание Определение промежутков возрастания и убывания функции (исследование функции на монотонность) Нахождение точек экстремума функции Построение
- 3. Исследование функции на монотонность (т.е. определение промежутков возрастания и убывания функции).
- 4. Исследовать функцию на монотонность – это значит выяснить, на каких промежутках из области определения функция возрастает,
- 5. Вспомним
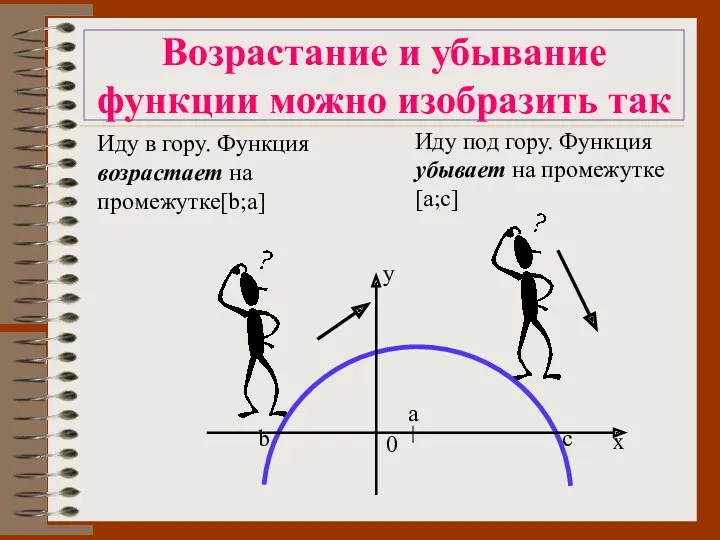
- 6. Возрастание и убывание функции можно изобразить так Иду в гору. Функция возрастает на промежутке[b;a] Иду под
- 7. Для определения промежутков возрастания и убывания функции можно использовать и производную .
- 8. Теорема: Если f(x) – непрерывна на промежутке и имеет f´(x), то а) если f´(x) > 0,
- 9. Алгоритм исследования функции на монотонность Найти производную функции f ΄(х) Найти стационарные (f ΄(х) = 0)
- 10. Определения Внутренние точки области определения функции, в которых производная функции равна нулю, называются стационарными. Внутренние точки
- 11. Например: найти промежутки монотонности функции f(x) = x³ - 6x² + 9x – 1 1) f´(x)
- 12. Найти промежутки монотонности функции у = 2х³ +3х² -100 у = х³ + 2х² + 6
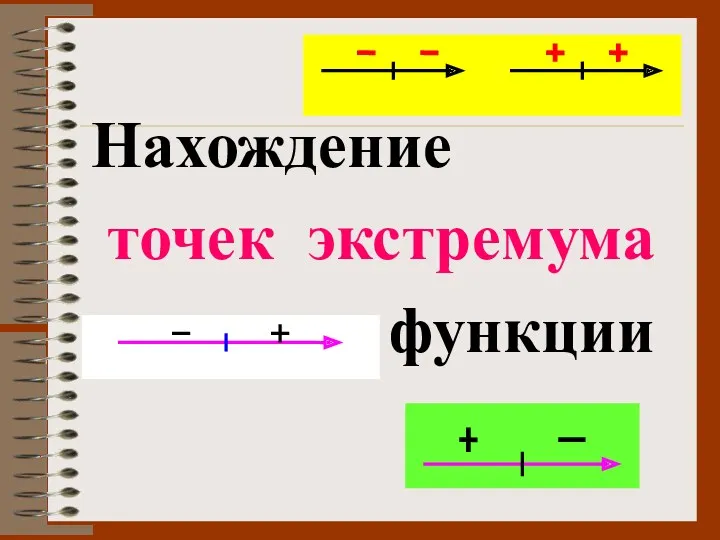
- 13. Нахождение точек экстремума функции
- 14. Определения Точка хо называется точкой минимума функции у = f(х), если у этой точки существует окрестность,
- 15. Определения Значение функции в точке максимума обозначают уmax (но на определенном участке вокруг точки максимума, а
- 16. Теорема Пусть функция у = f(х) непрерывна на промежутке Х и имеет внутри промежутка стационарную или
- 17. б) если у этой точки существует такая окрестность, в которой при х 0, а при х>х0
- 18. в) если у этой точки существует такая окрестность, что в ней и слева и справа от
- 19. Алгоритм нахождения точек экстремума функции Найти производную функции f ΄(х) Найти стационарные и критические точки функции
- 20. Например: найти точки экстремума функции Решение. 1) у΄=12 х³ - 48х² + 48х = = 12х(х²-4х+4)
- 21. Найдите точки экстремума функции и определите их характер у = 7 + 12х - х² у
- 22. Построение графиков функций
- 23. В тех случаях, когда речь идет о построении графика незнакомой функции или когда заранее трудно представить
- 24. План построения графика функции с помощью производной Найти область определения функции и определить точки разрыва если
- 25. Как найти промежутки выпуклости, вогнутости и точку перегиба графика функции Промежутки выпуклости и вогнутости кривой можно
- 26. Для нахождения интервалов выпуклости графика функции используют следующий алгоритм: Находят f΄(х), а затем f ΄΄(х) Находят
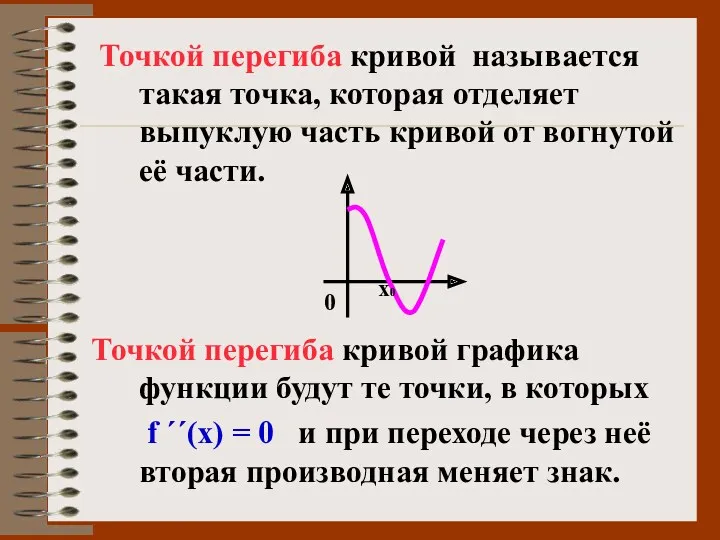
- 27. Точкой перегиба кривой называется такая точка, которая отделяет выпуклую часть кривой от вогнутой её части. Точкой
- 28. Найти интервалы выпуклости и точку перегиба функции Решение. Найдем у΄(х) и у΄΄(х): у΄(х) = 4х³-12х =>
- 29. Например: исследовать функцию у = 2х³+3х² -1 и построить её график Решение. D(у)= (-∞; +∞), четность
- 30. Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0; + ∞) - функция возрастает при
- 31. Найдем ещё некоторые точки (контрольные, дополнительные): т.к. х=-1 – точка максимума, то уmax=0 => (-1; 0)
- 32. Составим таблицу:
- 33. Найдем f ΄΄(х). f΄΄(х) =(6х(х+1))΄=12х+6 = 6(2х+1) f΄΄(х)=0 => 6(2х+1)=0 => х = -0,5 - точка
- 34. Построим график функции: х у 0 -1 -2 4 1 -5
- 35. Исследовать функцию и построить её график 1) у = 3х² - х³ 2) у = -
- 36. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
- 37. Теорема Дифференцируемая на (а;b) и непрерывная на [a;b] функция у=f(x) достигает своего наибольшего (наименьшего) значения на
- 38. Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у=f(х) на отрезке [а;в] 1) Найти производную f
- 39. Например: найти наименьшее и наибольшее значения функции у= х³ - 3х² - 45х + 1 на
- 40. Решение. б) на [-2;2] 1) у΄= 3х² - 6х – 45 2) у΄= 0 => 3х²
- 41. Самостоятельно найдите наименьшее и наибольшее значения функции у= х³ - 3х² - 45х + 1 на
- 42. Найдите наименьшее и наибольшее значения функции на заданном промежутке. 1) у = х²-8х+19 на [-1;5] 2)
- 43. Работа с графиками функций
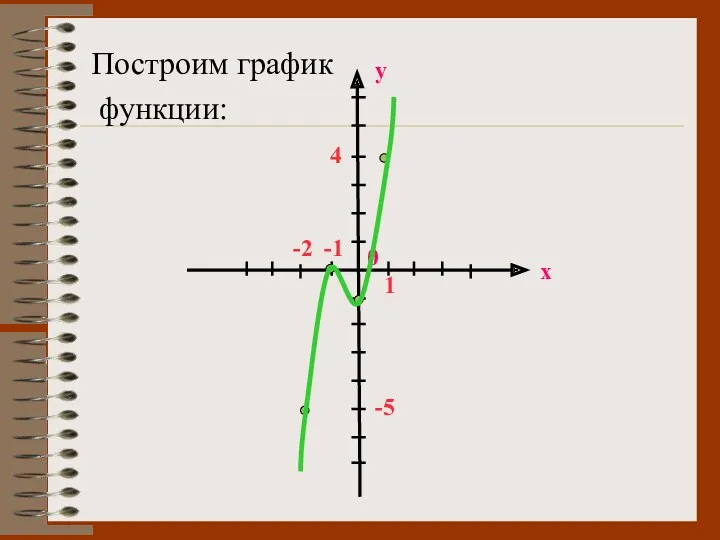
- 44. № 1. По графику функции ответьте на вопросы
- 45. 1) Отметьте стационарные точки. 2) Что можно сказать о производной в точке х1? 3) Назовите точки
- 46. Проверим ответы 1. (х1,х3,х4). 2. не существует. 3. (х2,х3,х4). 4. f′(х) ≤ 0. 5. [х2; х3]U
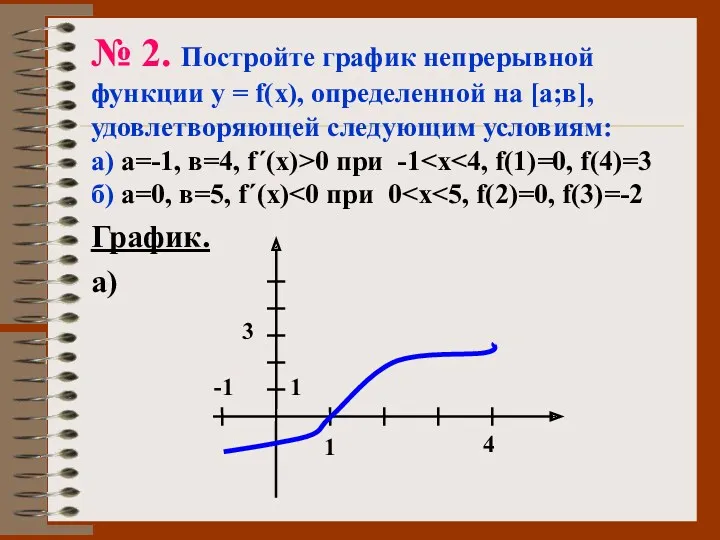
- 47. № 2. Постройте график непрерывной функции у = f(х), определенной на [а;в], удовлетворяющей следующим условиям: а)
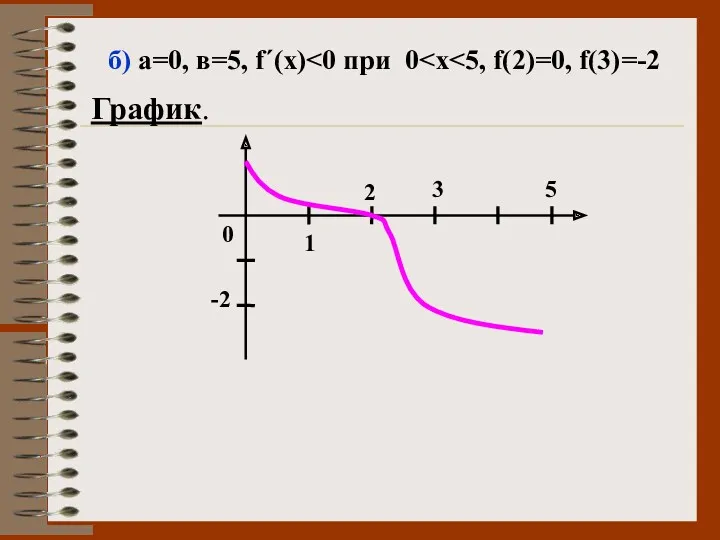
- 48. б) а=0, в=5, f΄(х) График. 0 -2 3 5 2 1
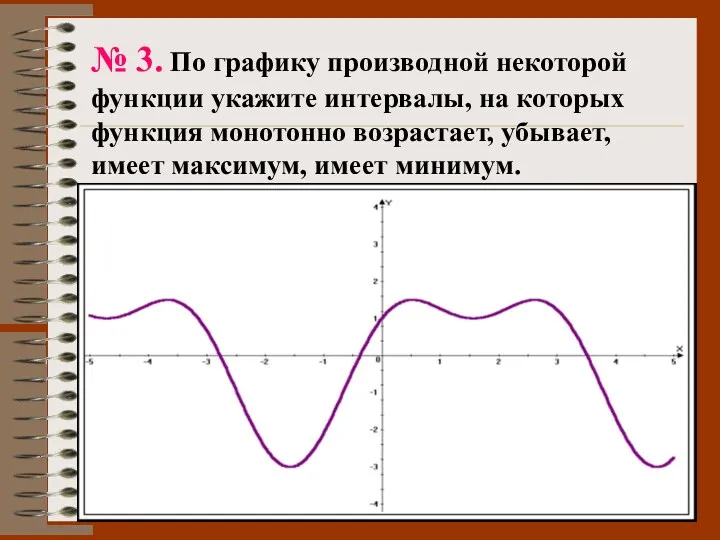
- 49. № 3. По графику производной некоторой функции укажите интервалы, на которых функция монотонно возрастает, убывает, имеет
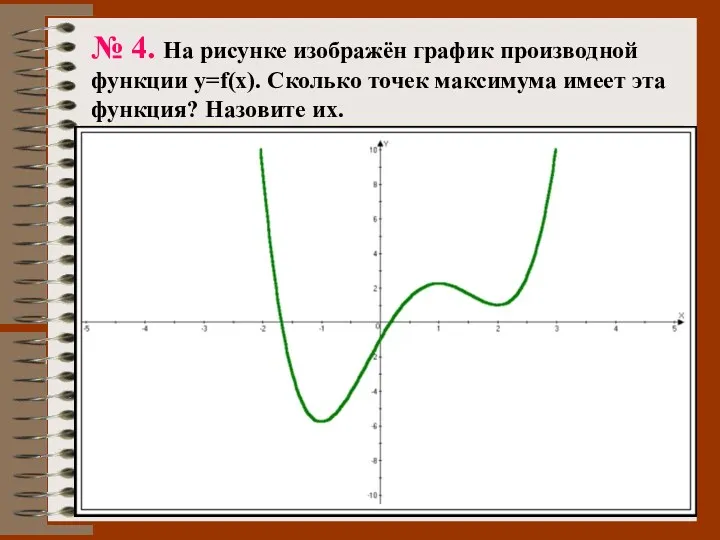
- 50. № 4. На рисунке изображён график производной функции y=f(x). Сколько точек максимума имеет эта функция? Назовите
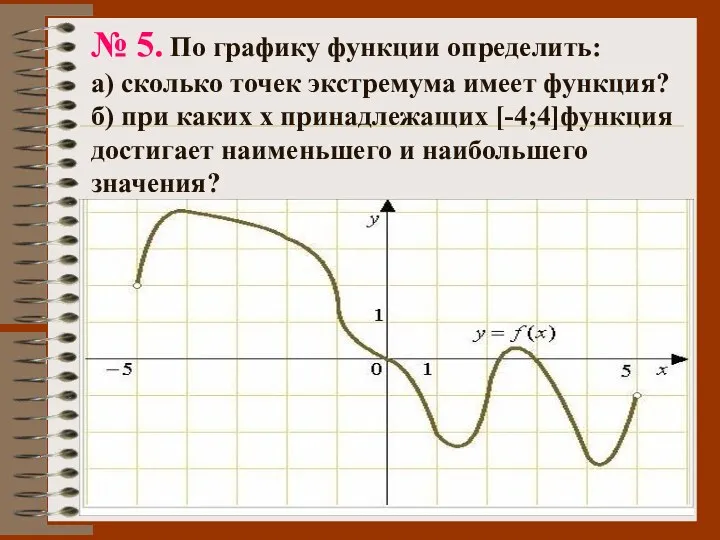
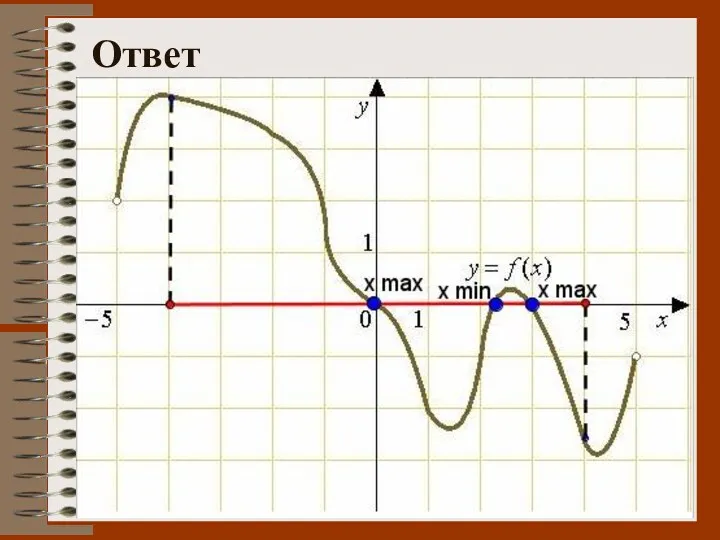
- 51. № 5. По графику функции определить: а) сколько точек экстремума имеет функция? б) при каких х
- 52. Ответ
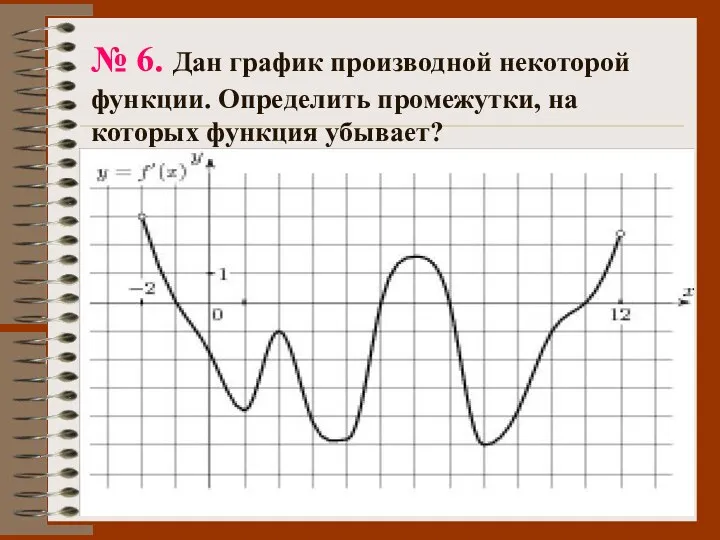
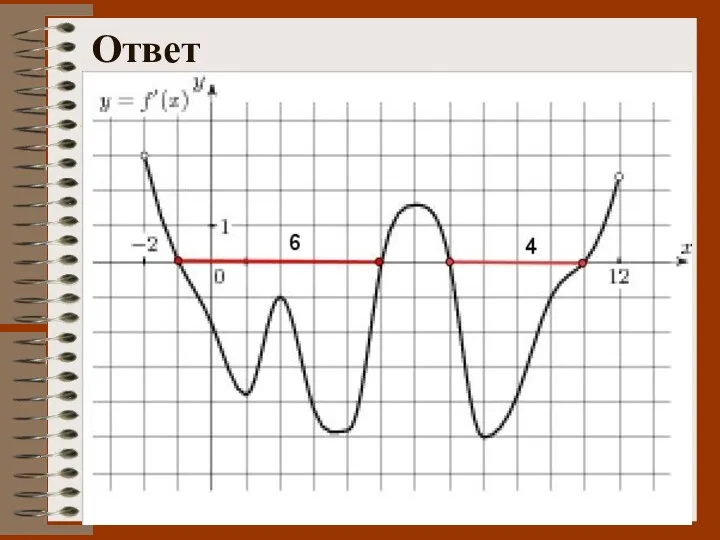
- 53. № 6. Дан график производной некоторой функции. Определить промежутки, на которых функция убывает?
- 54. Ответ
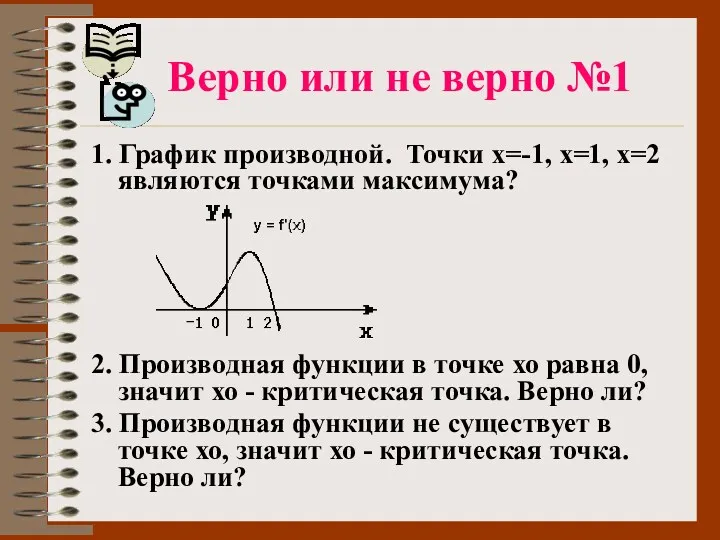
- 55. Верно или не верно №1 1. График производной. Точки х=-1, х=1, х=2 являются точками максимума? 2.
- 56. 4. Критическая точка является точкой экстремума. Верно ли? 5. Точка экстремума является критической точкой. Верно ли?
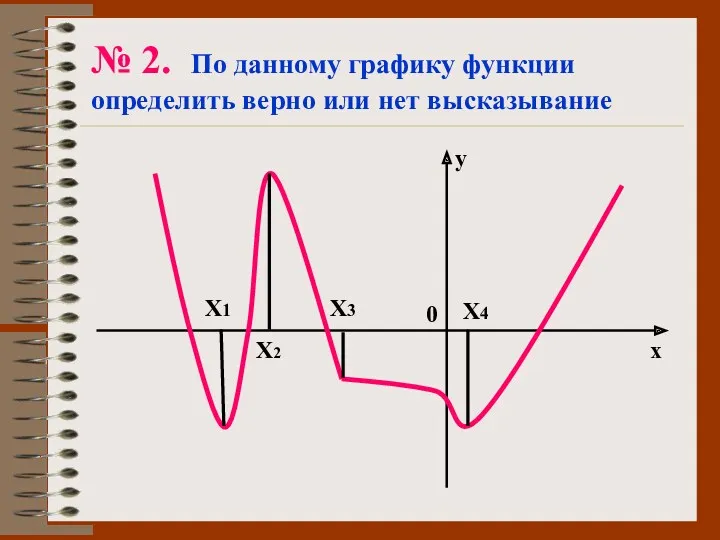
- 57. № 2. По данному графику функции определить верно или нет высказывание 0 х у Х1 Х2
- 58. Точка х1 – точка минимума. Точка х1 – точка перегиба. В точках х2 и х4 касательная
- 60. Скачать презентацию























![Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/591371/slide-29.jpg)





![Теорема Дифференцируемая на (а;b) и непрерывная на [a;b] функция у=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/591371/slide-36.jpg)


![Решение. б) на [-2;2] 1) у΄= 3х² - 6х –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/591371/slide-39.jpg)






 Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Математика навколо нас
Математика навколо нас Умножение многозначных чисел на двузначные
Умножение многозначных чисел на двузначные Веселая геометрия
Веселая геометрия Описательная статистика
Описательная статистика Роль математичного моделювання та розв’язування задач навколишнього світу
Роль математичного моделювання та розв’язування задач навколишнього світу Применение метода интервалов для решения неравенств
Применение метода интервалов для решения неравенств Математика. 1 класс. Урок 32. Числа 1-5 - Презентация
Математика. 1 класс. Урок 32. Числа 1-5 - Презентация Медиана числового набора. Устойчивость медианы
Медиана числового набора. Устойчивость медианы Подготовка к ГИА. Модуль Геометрия. Треугольники
Подготовка к ГИА. Модуль Геометрия. Треугольники Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Деление окружности на равные части путём перегибания круга
Деление окружности на равные части путём перегибания круга Методическая разработка открытого урока по математике по теме Луч. Пересечение линий. 1 класс. УМК Гармония
Методическая разработка открытого урока по математике по теме Луч. Пересечение линий. 1 класс. УМК Гармония Вычитание числа 4
Вычитание числа 4 Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость
Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость Составные задачи на нахождение неизвестного слагаемого
Составные задачи на нахождение неизвестного слагаемого Пересечение и объединение множеств
Пересечение и объединение множеств 1 класс. Интерактивный тренажер Брусничная полянка (вычитание числа 3)
1 класс. Интерактивный тренажер Брусничная полянка (вычитание числа 3) Занимательная математика
Занимательная математика Транспортная задача
Транспортная задача Загальні відомості про засоби вимірювань
Загальні відомості про засоби вимірювань Угол. Измерение углов. Виды углов
Угол. Измерение углов. Виды углов Презентация к уроку математики в 1 классе Многоугольники.
Презентация к уроку математики в 1 классе Многоугольники. Внеклассное мероприятие по математике для 8-9 классов (профориентация)
Внеклассное мероприятие по математике для 8-9 классов (профориентация) 20230917_prilozhenie_k_masterskoy_prezentatsiya
20230917_prilozhenie_k_masterskoy_prezentatsiya Теорема: средняя линия треугольника
Теорема: средняя линия треугольника Умножение и деление на 4
Умножение и деление на 4 Симетрія відносно точки
Симетрія відносно точки