Содержание
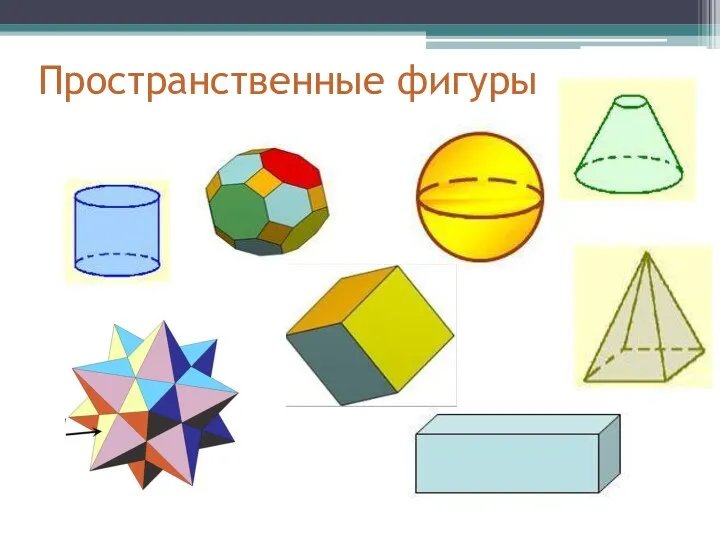
- 2. Пространственные фигуры
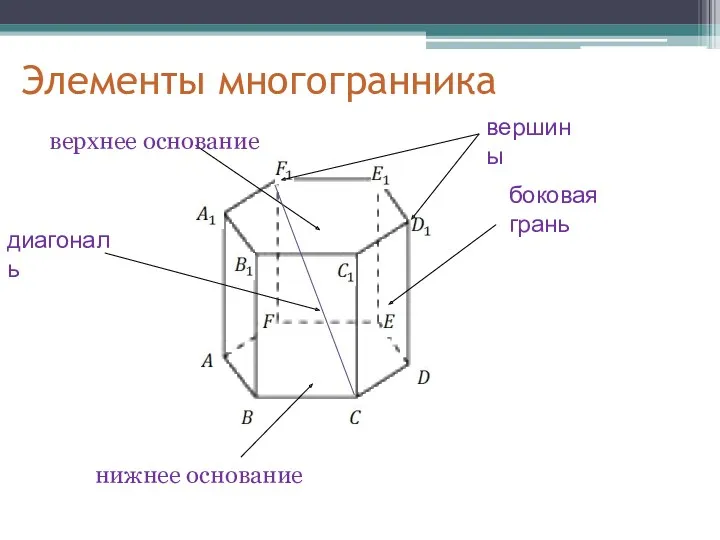
- 3. Элементы многогранника вершины верхнее основание нижнее основание боковая грань диагональ
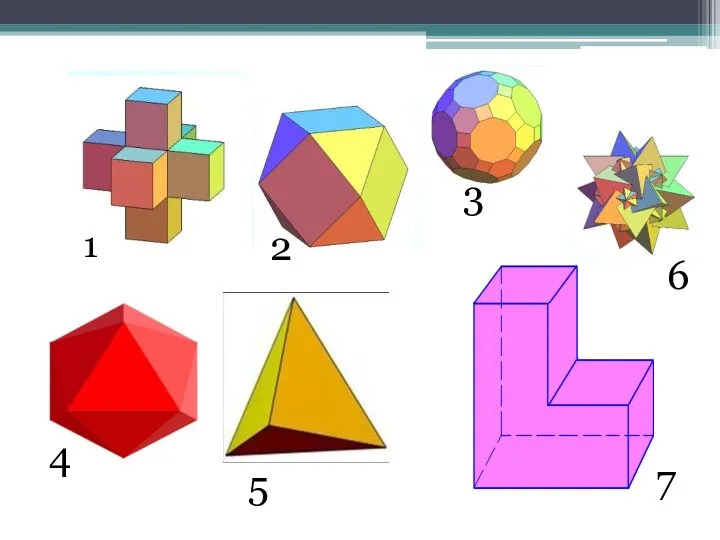
- 4. 1 2 3 4 5 6 7
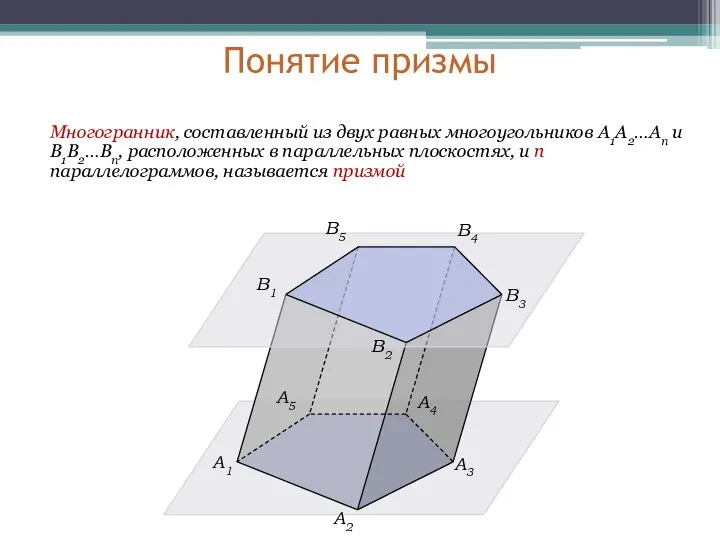
- 5. Понятие призмы Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и
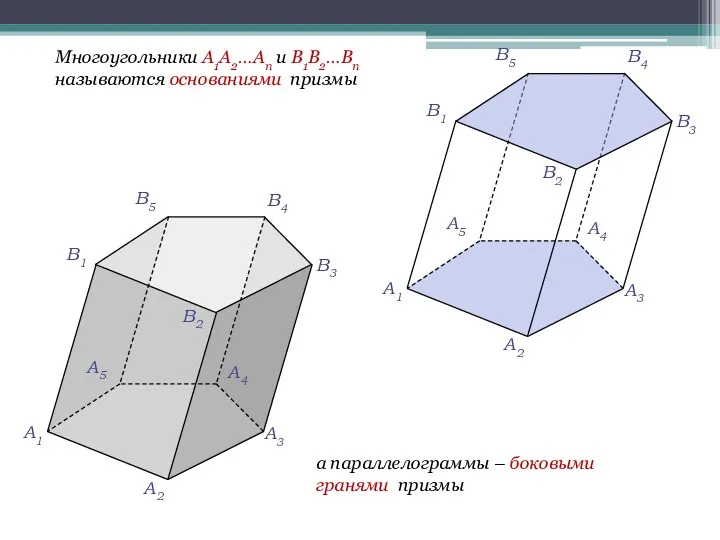
- 6. Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы а параллелограммы – боковыми гранями призмы A1 A2 A3
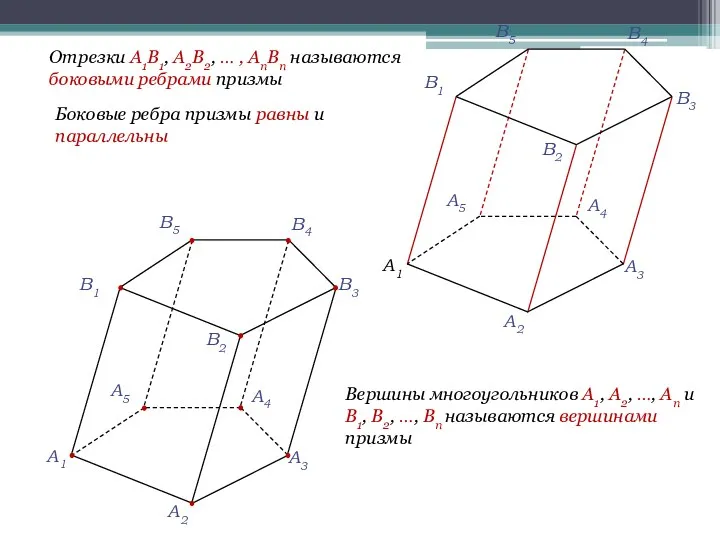
- 7. Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы Боковые ребра призмы равны и параллельны
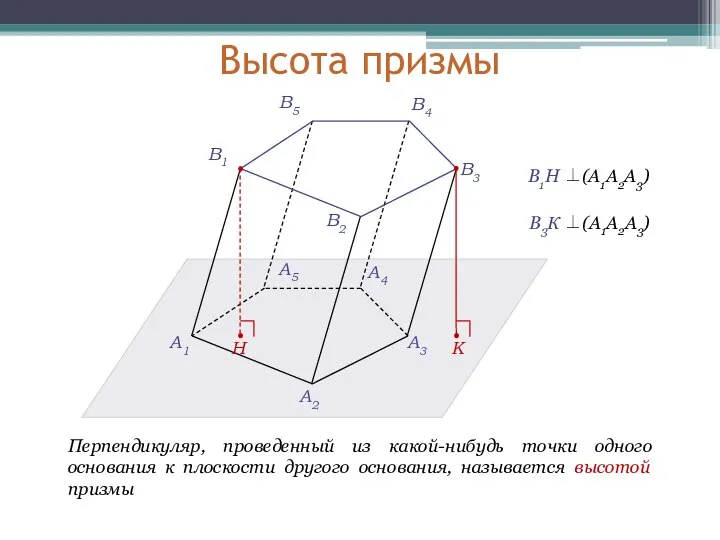
- 8. Высота призмы A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 К Н Перпендикуляр, проведенный
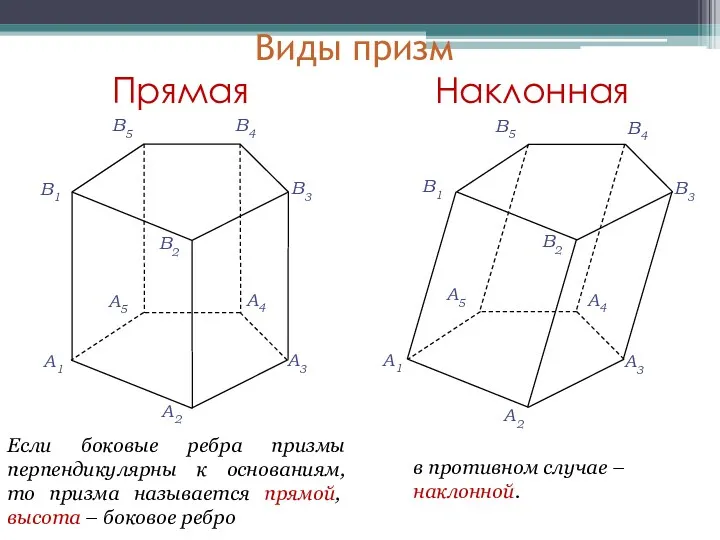
- 9. Виды призм A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 Если боковые ребра призмы
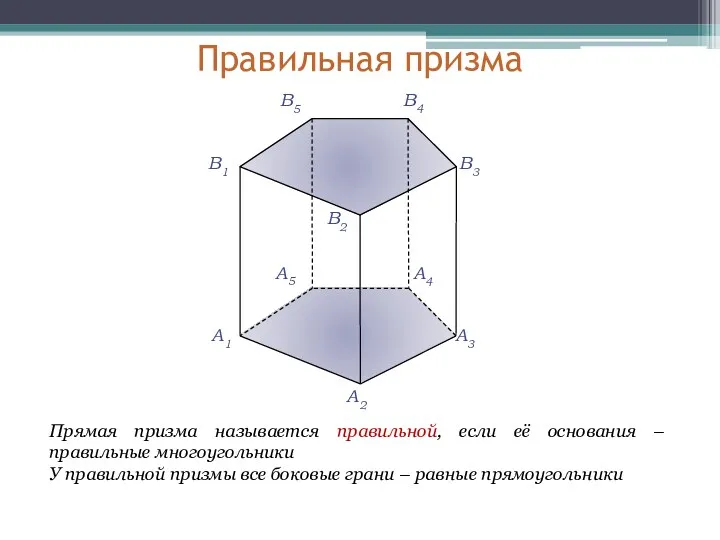
- 10. Правильная призма A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 Прямая призма называется правильной,
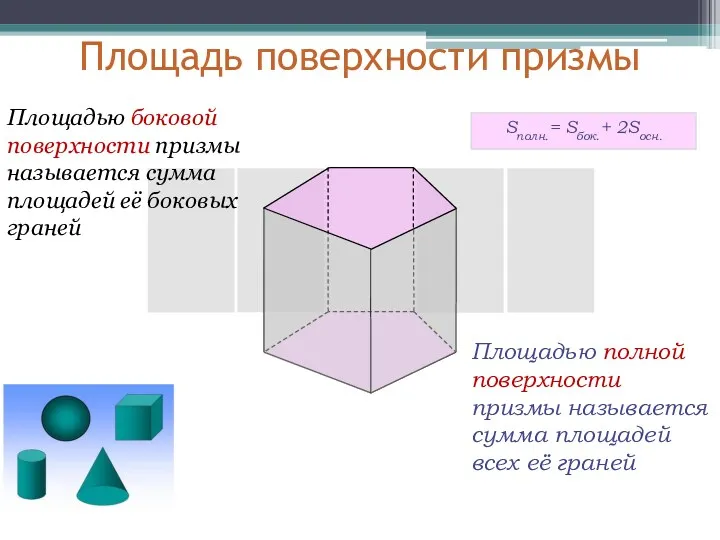
- 11. Площадью боковой поверхности призмы называется сумма площадей её боковых граней Площадью полной поверхности призмы называется сумма
- 12. Теорема о площади боковой поверхности прямой призмы Площадь боковой поверхности прямой призмы равна произведению периметра основания
- 15. Скачать презентацию


 Многозначные числа.
Многозначные числа. Урок математики в 4 классе (Л.Занков) по теме Округление чисел
Урок математики в 4 классе (Л.Занков) по теме Округление чисел Рациональные дроби. Открытый урок
Рациональные дроби. Открытый урок Арифметик прогрессия. 9 класс
Арифметик прогрессия. 9 класс Раскрытие скобок и приведение подобных слагаемых
Раскрытие скобок и приведение подобных слагаемых Исследовательская работа по математике: Математика в профессиях наших родителей. 5 класс
Исследовательская работа по математике: Математика в профессиях наших родителей. 5 класс Углы и многоугольники
Углы и многоугольники Сравнение дробей
Сравнение дробей Презентация по теме: Числа от 1 до 10
Презентация по теме: Числа от 1 до 10 Метрология. Калибровка средств измерений. (Лекция 4)
Метрология. Калибровка средств измерений. (Лекция 4) Правильный додекаэдр
Правильный додекаэдр Линейная функция и ее график
Линейная функция и ее график открытый урок по математике Объём прямоугольного параллелепипеда 3 класс
открытый урок по математике Объём прямоугольного параллелепипеда 3 класс Вклад математиков в победу Великой Отечественной Войне
Вклад математиков в победу Великой Отечественной Войне Округление натуральных чисел
Округление натуральных чисел Объем Иванова и Макарова
Объем Иванова и Макарова Координатный угол. 4 класс
Координатный угол. 4 класс Үш перпендикуляр туралы теорема
Үш перпендикуляр туралы теорема Интегрированный урок по математике и ПДД
Интегрированный урок по математике и ПДД Презентация для детей Название геометрических предметов
Презентация для детей Название геометрических предметов Длина окружности
Длина окружности Прямоугольный параллелепипед. Тетраэдр. Решение задач
Прямоугольный параллелепипед. Тетраэдр. Решение задач Равносильные уравнения
Равносильные уравнения Признаки равенства треугольников. Равнобедренный треугольник. Повторение и закрепление пройденного материала
Признаки равенства треугольников. Равнобедренный треугольник. Повторение и закрепление пройденного материала Тест на тему: Четырехугольники
Тест на тему: Четырехугольники Сложение и вычитание смешанных чисел (5 класс)
Сложение и вычитание смешанных чисел (5 класс) Табличные случаи умножения и деления
Табличные случаи умножения и деления Тест по математике Решение логических задач. 5 класс
Тест по математике Решение логических задач. 5 класс