Содержание
- 2. Определение производной Пусть функция y = f(x) определена в некотором интервале (a; b). Аргументу x придадим
- 3. Определение производной Итак, по определению: Функция y = f(x) , имеющая производную в каждой точке интервала
- 4. Геометрический смысл производной Возьмем на непрерывной кривой L две точки М и М1: х f(x )
- 5. Геометрический смысл производной Производная f ’(x) равна угловому коэффициенту касательной к графику функции y = f(x)
- 6. Связь между непрерывностью и дифференцируемостью функции Если функция f(x) дифференцируема в некоторой точке , то она
- 7. Правила дифференцирования Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 8. Производная сложной функции Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x))
- 9. Производная неявно заданной функции Если функция задана уравнением y = f(х) , разрешенным относительно y, то
- 10. Логарифмическое дифференцирование В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем результат
- 12. Скачать презентацию





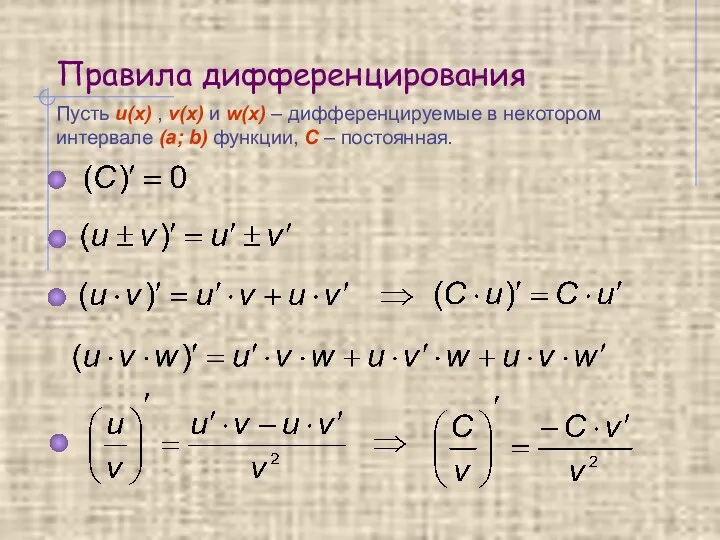



 Какие дроби называются неправильными?
Какие дроби называются неправильными? Математическая викторина (8 класс)
Математическая викторина (8 класс) Определенный интеграл. Формула интегрирования по частям (пример 2)
Определенный интеграл. Формула интегрирования по частям (пример 2) Построение сечений тетраэдра и параллелепипеда. 10 класс
Построение сечений тетраэдра и параллелепипеда. 10 класс Итоговый тест по математике, 1 класс
Итоговый тест по математике, 1 класс Задачи на увеличение числа в несколько раз
Задачи на увеличение числа в несколько раз Урок математики Закрепление изученного материала. Зимняя олимпиада в Сочи.
Урок математики Закрепление изученного материала. Зимняя олимпиада в Сочи. Основные правила комбинаторики
Основные правила комбинаторики Полезные факты и теоремы
Полезные факты и теоремы Задачи на готовых чертежах. Второй признак равенства треугольников
Задачи на готовых чертежах. Второй признак равенства треугольников 102. Случаи сложения вида +6
102. Случаи сложения вида +6 Конус. Понятие конуса и его элементы
Конус. Понятие конуса и его элементы Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера Урок математики Решение задач 4 класс
Урок математики Решение задач 4 класс ПрезентацияПутешествие в страну Математики
ПрезентацияПутешествие в страну Математики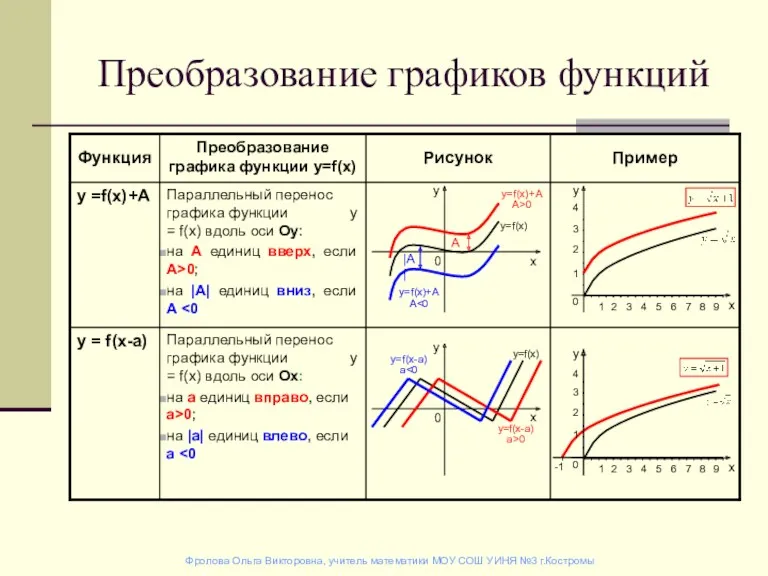 Преобразование графиков функций
Преобразование графиков функций Параллельность двух прямых в пространстве
Параллельность двух прямых в пространстве Геометричні перетворення
Геометричні перетворення Теорема Пифагора. Решение задач
Теорема Пифагора. Решение задач Формулы приведения
Формулы приведения Счет 1, 2, 3
Счет 1, 2, 3 Правило Лопиталя
Правило Лопиталя Устный счет
Устный счет Обыкновенные дроби. Урок-вернисаж
Обыкновенные дроби. Урок-вернисаж Линейное уравнение с одной переменной. Что называется уравнением?
Линейное уравнение с одной переменной. Что называется уравнением?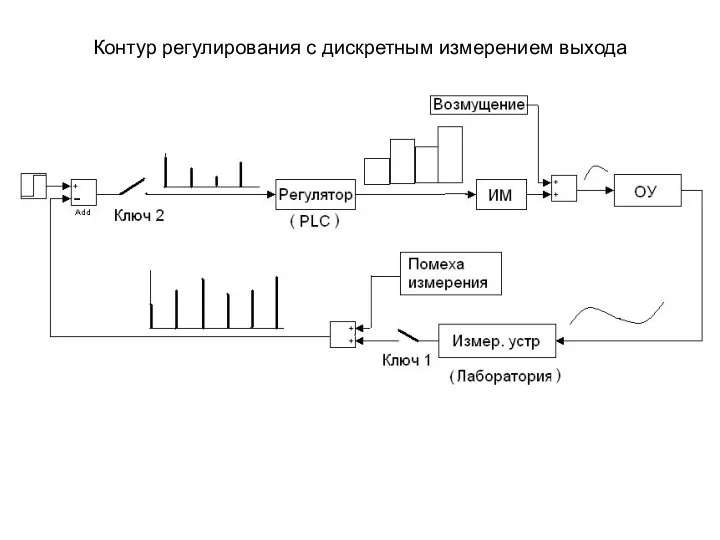 Непрерывная и дискретная модели непрерывной динамической системы. (Тема 9)
Непрерывная и дискретная модели непрерывной динамической системы. (Тема 9) Как писать цифры. 1 класс
Как писать цифры. 1 класс Миллион
Миллион