Содержание
- 2. Цели урока: ОБУЧАЮЩАЯ: 1) Ввести определение производной функции на основе задач физики, рассматривая при этом физический
- 3. Вопросы: История возникновения производной функции. Понятие производной. Геометрический смысл производной. Физический (механический) смысл производной.
- 4. 1. История возникновения производной функции Раздел математики, в котором изучаются производные и их применение к исследованию
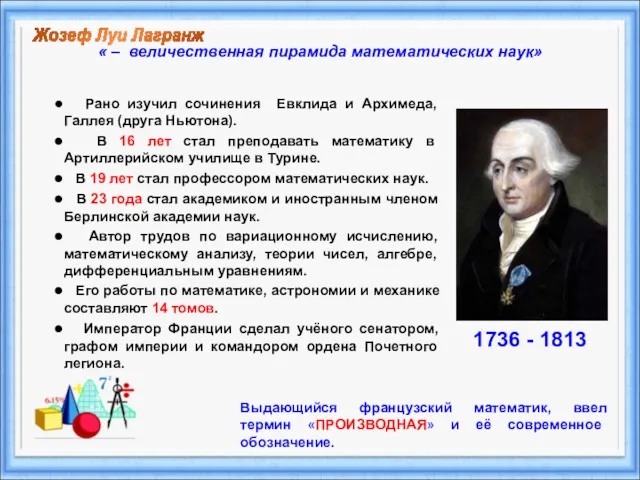
- 5. Рано изучил сочинения Евклида и Архимеда, Галлея (друга Ньютона). В 16 лет стал преподавать математику в
- 9. 2. Понятие производной Пусть х - произвольная точка, лежащая в некоторой окрестности точки х0 (окрестность точки
- 10. Производной функции y=f(x) в точке х0 называется предел отношения приращения функции ∆f к приращению аргумента ∆x,
- 11. 2. Понятие производной Четыре обозначения для производной:
- 12. 2. Понятие производной
- 13. Правило нахождения производной функции y=f(x) в точке х0: Найти значение функции в точке x0+∆x: f(x0+∆x) Найти
- 14. Пример: Дана функция y=x2. Найти её производную в произвольной точке и в точке х=3. Решение: f(x0+∆x)=(х+∆x)2;
- 15. Пример: Воспользовавшись определением производной, найти производную функции Решение: Дадим x приращение Δx, тогда y получит приращение
- 16. Электронная физминутка для глаз
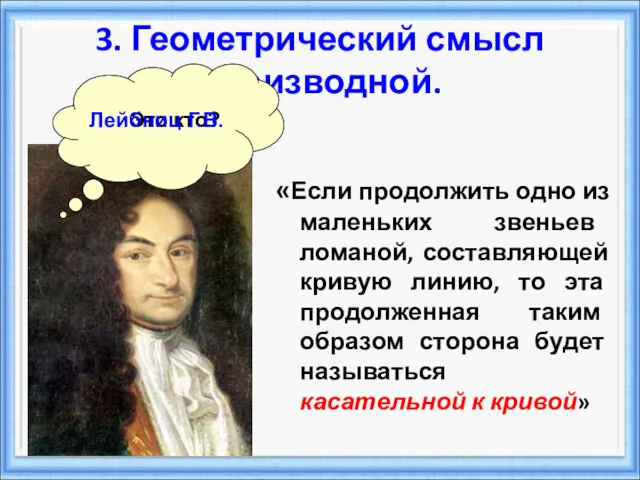
- 18. «Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная таким образом сторона
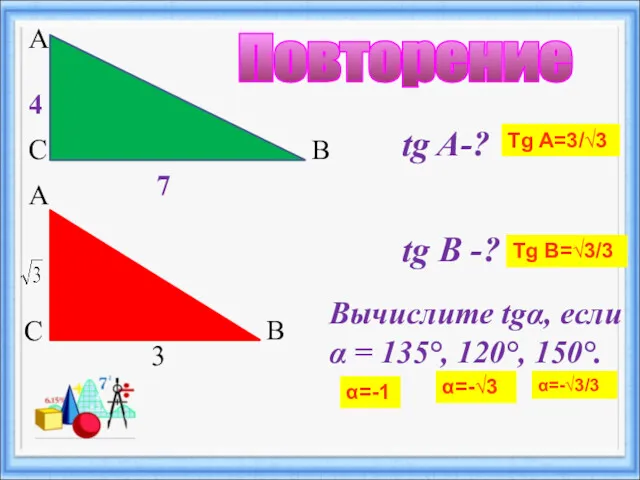
- 19. А С В tg A-? tg В -? 4 7 А В С 3 Вычислите tgα,
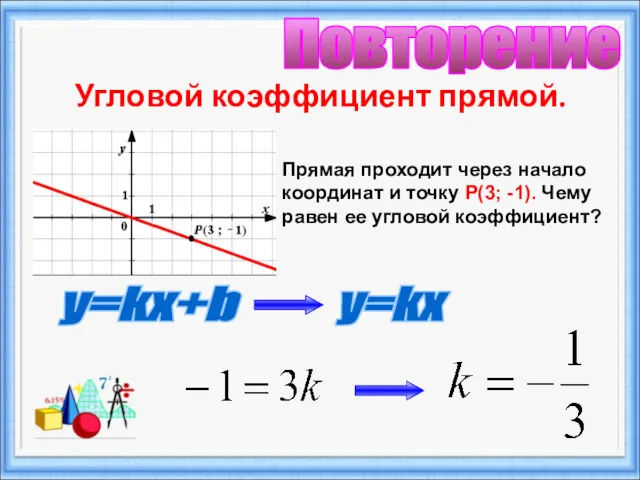
- 20. Угловой коэффициент прямой. Прямая проходит через начало координат и точку Р(3; -1). Чему равен ее угловой
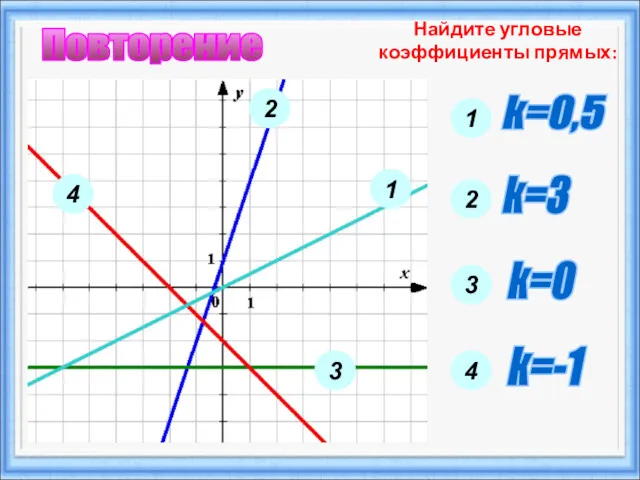
- 21. Найдите угловые коэффициенты прямых: 2 1 3 4 1 k=0,5 2 k=3 3 k=0 4 k=-1
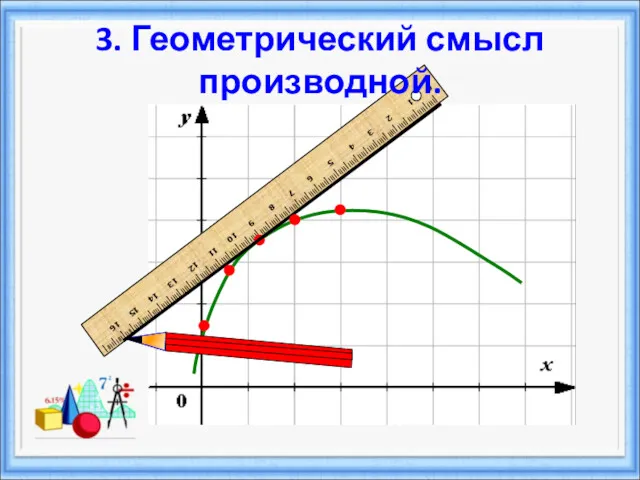
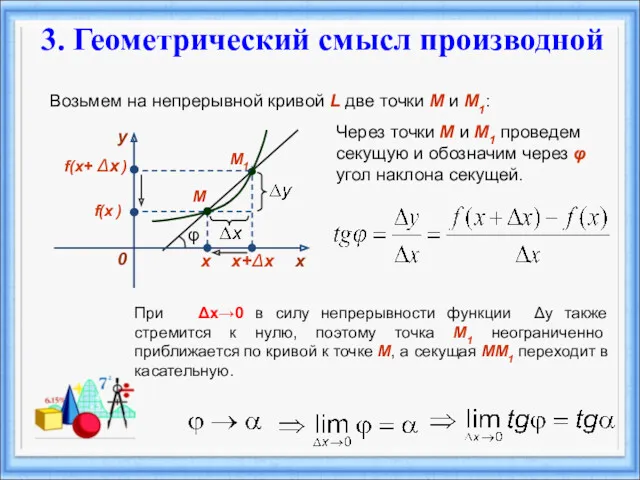
- 22. 3. Геометрический смысл производной.
- 23. 3. Геометрический смысл производной Возьмем на непрерывной кривой L две точки М и М1: х f(x
- 24. Производная f ’(x) равна угловому коэффициенту касательной к графику функции y = f(x) в точке, абсцисса
- 25. 13.11.2020 Пример: Найти уравнение касательной и нормали для функции f(x)=x2 в точке x0 = 3. Решение:
- 26. «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад»
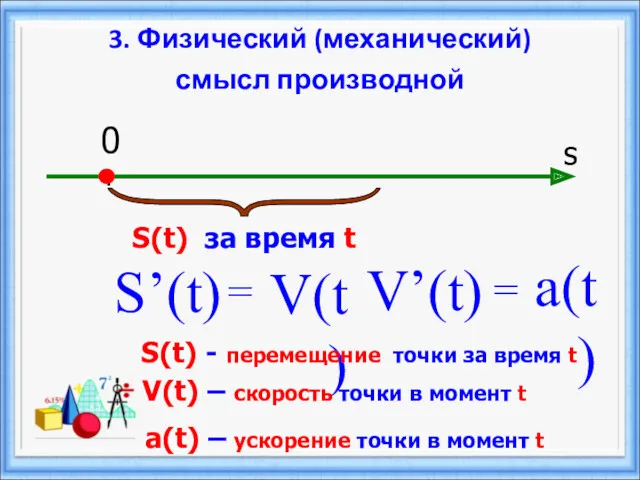
- 27. 3. Физический (механический) смысл производной
- 28. Пример: Точка движется прямолинейно по закону S(t) = 2 t ³ - 3 t. Вычислите скорость
- 29. Решение: t = 2,2 (с). 3. Физический (механический) смысл производной
- 30. Пример: Материальная точка движется прямолинейно по закону х(t)=t³- 4t² Найдите скорость и ускорение в момент времени
- 31. 2. Найти мгновенную скорость в момент времени t=3 сек. 3. Найти ускорение при t=3 сек 1.
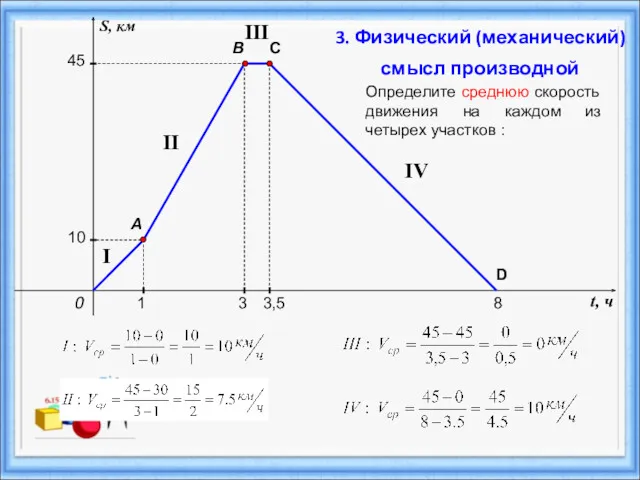
- 32. t, ч S, км 0 A B 1 10 3 3,5 8 C 45 D I
- 33. Пример: Две материальные точки движутся прямолинейно по законам s1(t) = 1 - 6t + 2,5t 2
- 34. Пример: Пусть количество вещества, вступившего в химическую реакцию задается зависимостью р( t ) = t 2/2
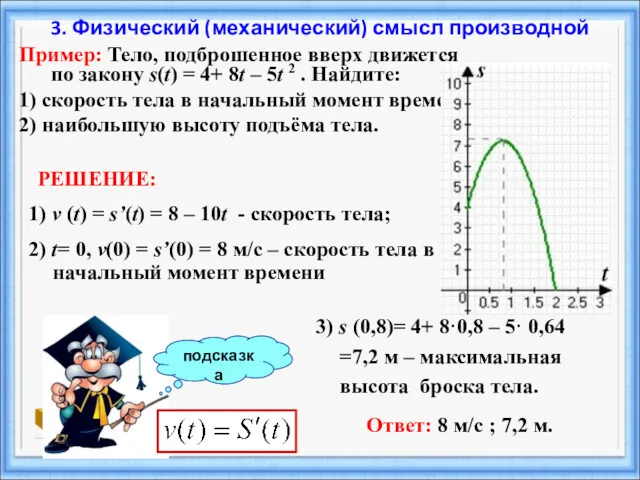
- 35. подсказка Пример: Тело, подброшенное вверх движется по закону s(t) = 4+ 8t – 5t 2 .
- 36. Точка движется прямолинейно по закону S (t) = t3 – 2t2. Выберите какой из формул задается
- 37. Объем продукции V цеха в течение дня зависит от времени по V(t) = -5/3t3+15/2t2+50t+70. Вычислите производительность
- 38. Подведём итог: Что называется касательной к графику функции в точке? В чем заключается геометрический смысл производной?
- 39. тревожно, не уверен в себе спокойно, у меня все получится безразлично, что будет, то и будет
- 40. Домашнее задание: Написать конспект занятия. Выделить формулы и определения. 13.11.2020
- 42. Скачать презентацию


























 Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА
Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА Путешествие по Горному Алтаю. Проценты (интегрированный урок). 5 класс
Путешествие по Горному Алтаю. Проценты (интегрированный урок). 5 класс Полный факторный эксперимент
Полный факторный эксперимент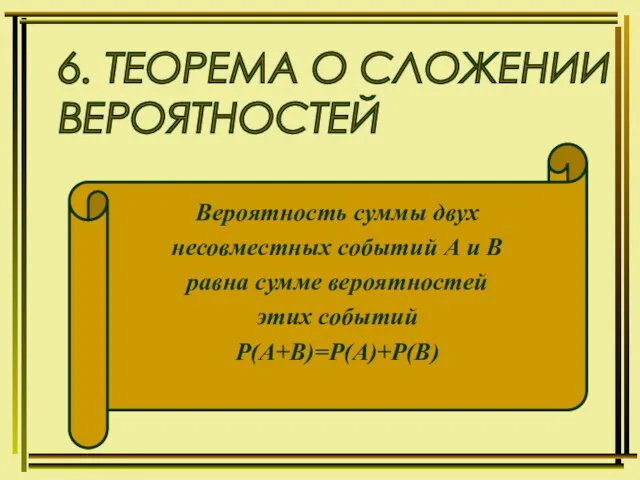 Теорема о сложении вероятностей
Теорема о сложении вероятностей Транспортные задачи
Транспортные задачи Сложение в столбик в пределах 100 (2класс)
Сложение в столбик в пределах 100 (2класс) Математика. 4 класс. Итоговое повторение (тест)
Математика. 4 класс. Итоговое повторение (тест) Решение неравенств методом интервалов
Решение неравенств методом интервалов Формулы сокращённого умножения. 7 класс
Формулы сокращённого умножения. 7 класс Экстремумы функции
Экстремумы функции Виды призм. Площадь поверхности призм
Виды призм. Площадь поверхности призм Центральная симметрия
Центральная симметрия Пространство. Трехмерное пространство
Пространство. Трехмерное пространство Случайная изменчивость
Случайная изменчивость Математическое моделирование. Значимость коэффициентов регрессии
Математическое моделирование. Значимость коэффициентов регрессии Случаи сложения вида +6
Случаи сложения вида +6 Подготовка учащихся к ОГЭ по математике
Подготовка учащихся к ОГЭ по математике Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Многочлен. Урок математики 7 класс
Многочлен. Урок математики 7 класс Умножение десятичных дробей
Умножение десятичных дробей Занимательная математика Геометрические фигуры
Занимательная математика Геометрические фигуры Средние величины
Средние величины Статистика по опросу студентов, проходивших практику
Статистика по опросу студентов, проходивших практику Математическая игра Магия чисел
Математическая игра Магия чисел Построение правильных многоугольников с помощью циркуля и линейки
Построение правильных многоугольников с помощью циркуля и линейки Определение геометрической прогрессии
Определение геометрической прогрессии Оценка статистических характеристик
Оценка статистических характеристик Игра Помоги поросятам спрятаться от волка
Игра Помоги поросятам спрятаться от волка