Задача 3. О скорости химической реакции
Пусть некоторое вещество вступает в
химическую реакцию. Количество этого вещества Q изменяется в течение реакции в зависимости от времени t и является функцией от времени.
Пусть за время ∆t количество вещества изменяется на ∆Q , тогда отношение будет выражать среднюю скорость химической реакции за время ∆t.
Предел этого отношения - это скорость химической реакции в данный момент времени t.
Задача 4. О скорости радиоактивного распада
Если m - масса радиоактивного вещества и t - время, то явление радиоактивного распада в момент времени t при условии, что масса радиоактивного вещества с течением времени уменьшается, характеризуется функцией m= m(t).
Средняя скорость распада за время ∆t выражается отношением
а мгновенная скорость распада в момент времени t -
.
II. Задачи, приводящие к понятию производной



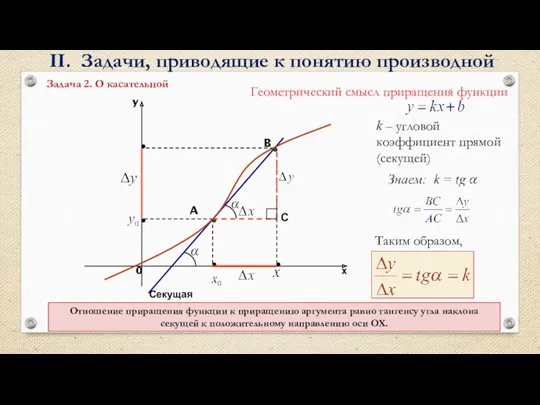
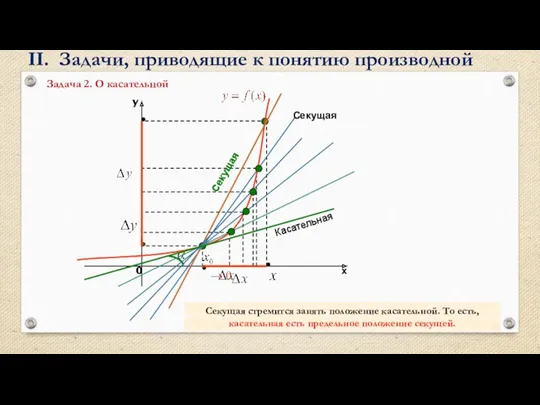
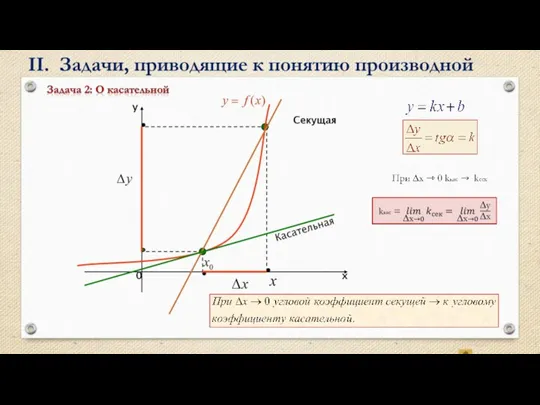


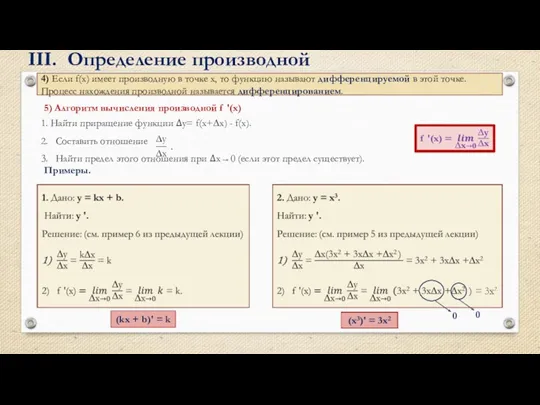

 Среднее арифметическое
Среднее арифметическое Презентация к уроку математики Письменное сложение и вычитание с переходом через десяток 2 класс УМК Школа России
Презентация к уроку математики Письменное сложение и вычитание с переходом через десяток 2 класс УМК Школа России Презентация Дифференцированный подход при обучении математике
Презентация Дифференцированный подход при обучении математике Презентация Счёт в пределах 1000
Презентация Счёт в пределах 1000 Применение нескольких способов разложения многочленов на множители
Применение нескольких способов разложения многочленов на множители Умножение многочлена на одночлен
Умножение многочлена на одночлен Исследование операций. Основы теории игр
Исследование операций. Основы теории игр Занимательная математика (средняя группа)
Занимательная математика (средняя группа) презентация Веселый Счет
презентация Веселый Счет Такие нужные проценты
Такие нужные проценты Логика высказываний
Логика высказываний Окружность. Дети. Своя игра
Окружность. Дети. Своя игра Математика 4 класс. Тест
Математика 4 класс. Тест Определенный интеграл
Определенный интеграл Вычисление объемов
Вычисление объемов Математический КВН
Математический КВН Математика. Повтороение. Урок 2
Математика. Повтороение. Урок 2 Зеркальное отражение предметов
Зеркальное отражение предметов Задачи на движение
Задачи на движение Теорема Виета
Теорема Виета Прямоугольный параллелепипед
Прямоугольный параллелепипед Правила дифференцирования. Производная функции
Правила дифференцирования. Производная функции Деление на двузначное число
Деление на двузначное число задачи на нахождение целого или части
задачи на нахождение целого или части Периметр многоугольника
Периметр многоугольника Презентация Свойства четырехугольников для внеклассного занятия во 2 классе
Презентация Свойства четырехугольников для внеклассного занятия во 2 классе алгебра 7 класс
алгебра 7 класс Презентация к уроку по теме Сложение и вычитание в пределах 20 Диск
Презентация к уроку по теме Сложение и вычитание в пределах 20 Диск