Содержание
- 2. Высказывания Определение 1 Высказывание – это повествовательное предложение, которое является либо истинным, либо ложным, но не
- 3. Высказывания Пример 1 Все предложения, приведенные ниже, являются высказываниями. Минск – столица Беларуси. Марсель – столица
- 4. Высказывания Пример 2 Предложения, приведенные ниже, не являются высказываниями. Который час? Вам следует внимательно слушать лекцию.
- 5. Высказывания
- 6. Высказывания Раздел логики, изучающий высказывания, называется исчислением высказываний или пропозициональной логикой. Греческий философ Аристотель, живший более
- 7. Сложные высказывания Рассмотрим методы построения новых высказываний из данных высказываний. Эти методы были изложены английским математиком
- 8. Сложные высказывания Новые высказывания, называемые сложными высказываниями, строятся из уже имеющихся высказываний с помощью логических операций.
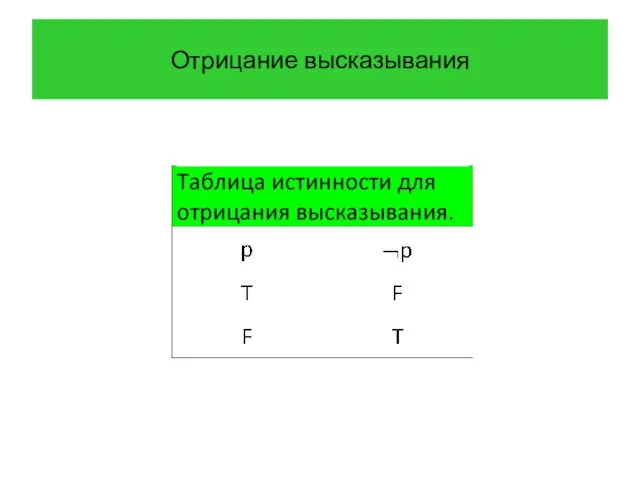
- 9. Отрицание высказывания
- 10. Отрицание высказывания
- 11. Отрицание высказывания Пример 3 Построить отрицание высказывания «Смартфон Анны имеет не менее 32 GB памяти» и
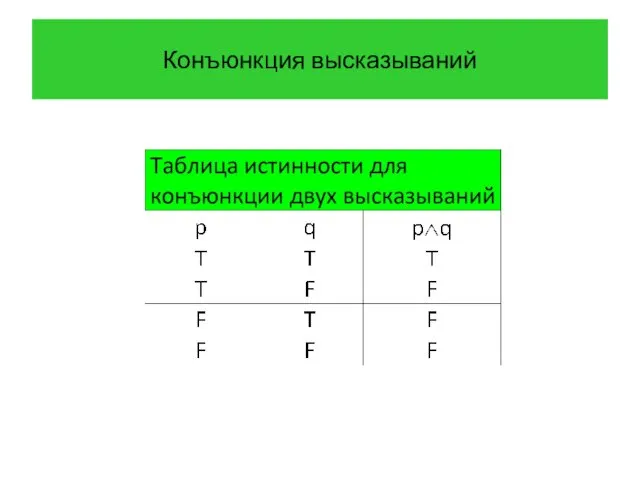
- 12. Конъюнкция высказываний Определение 3 Конъюнкцией высказываний p и q называется высказывание «p и q», которое обозначается
- 13. Конъюнкция высказываний
- 14. Конъюнкция высказываний Пример 4 Построить конъюнкцию высказываний p и q, где p – высказывание «На персональном
- 15. Конъюнкция высказываний Решение Конъюнкция высказываний p и q: «На персональном компьютере Андрея свободно более 16 GB
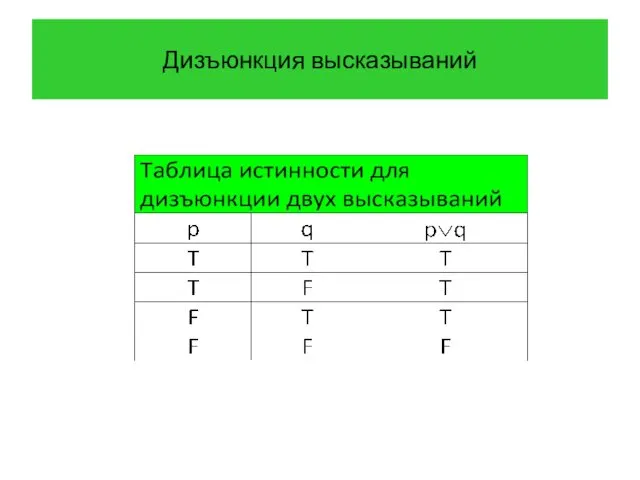
- 16. Дизъюнкция высказываний Определение 4 Дизъюнкцией высказываний p и q называется высказывание «p или q», которое обозначается
- 17. Дизъюнкция высказываний
- 18. Дизъюнкция высказываний Пример 5 Построить дизъюнкцию высказываний p и q, где p – высказывание «На персональном
- 19. Дизъюнкция высказываний Решение. Дизъюнкция высказываний p и q: «На персональном компьютере Андрея свободно более 16 GB
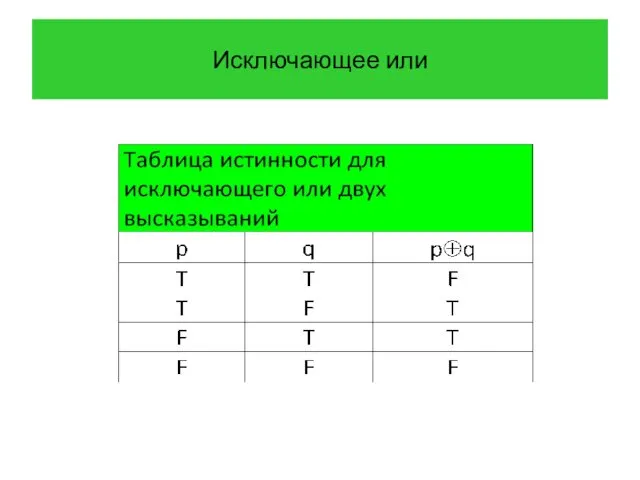
- 20. Исключающее или Определение 5 Исключающим или высказываний p и q называется высказывание «p или q, но
- 21. Исключающее или
- 22. Исключающее или Пример 6 Исключающее или используется в следующей ситуации. Студенты изучающие математический анализ или программирование,
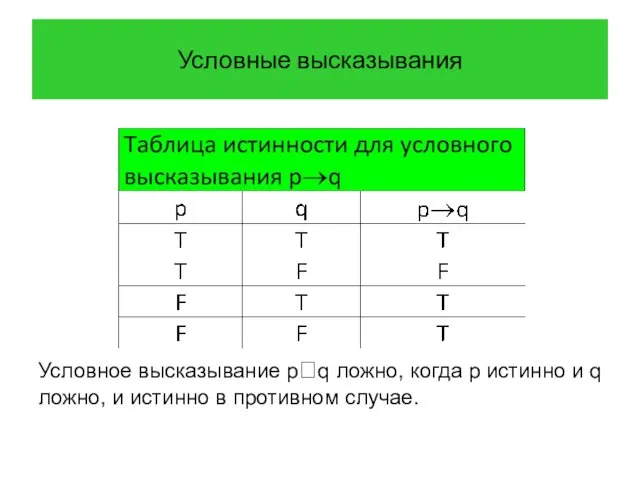
- 23. Условные высказывания Определение 6 Пусть p и q – два высказывания. Высказывание «если p, то q»
- 24. Условные высказывания Условное высказывание pq ложно, когда p истинно и q ложно, и истинно в противном
- 25. Условные высказывания
- 26. Условные высказывания Пример 7 Пусть p – высказывание «Мария изучает дискретную математику», а q – высказывание
- 27. Конверсия, контрапозиция, инверсия С условным высказыванием p q связаны еще три условных высказывания: высказывание q
- 28. Конверсия, контрапозиция, инверсия Пример 7 Пусть p – высказывание «Футбольный клуб «Неман» выигрывает матч», а q
- 29. Биимпликация высказываний Определение 7 Биимпликацией высказываний p и q называется высказывание «p тогда и только тогда,
- 30. Биимпликация высказываний Биимпликация p q истинна, когда оба высказывания p и q одновременно истинны или
- 31. Биимпликация высказываний Биимпликацию p q можно выразить с помощью следующих оборотов речи: p необходимо и
- 32. Биимпликация высказываний Пример 8 Пусть p – высказывание «Вы можете полететь из Минска в Париж на
- 33. Таблицы истинности сложных высказываний С помощью введенных логических операций конъюнкция, дизъюнкция, исключающее или, импликация, биимпликация и
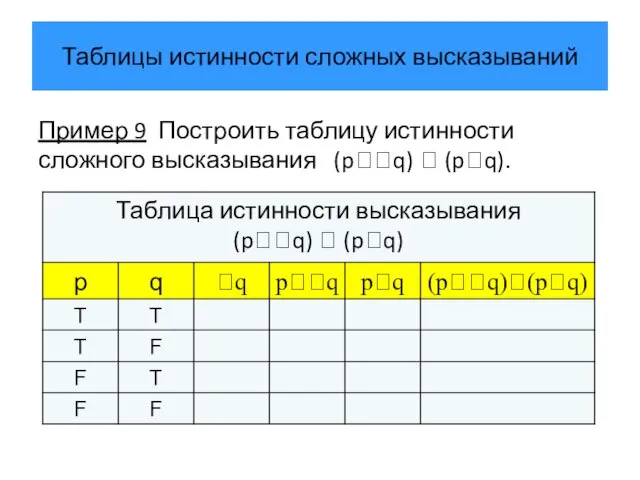
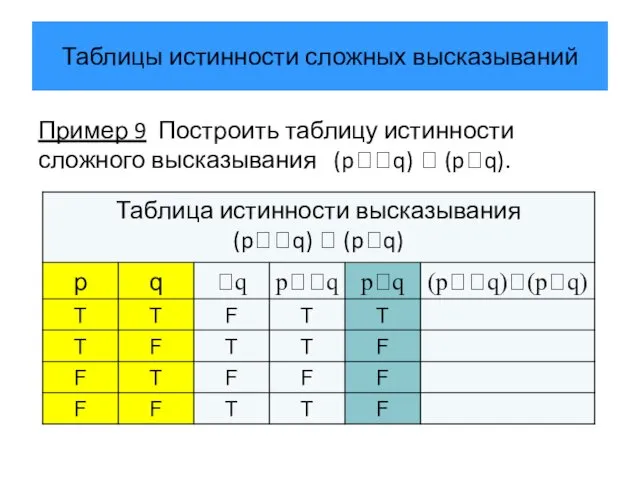
- 34. Таблицы истинности сложных высказываний Пример 9 Построить таблицу истинности сложного высказывания (pq) (pq).
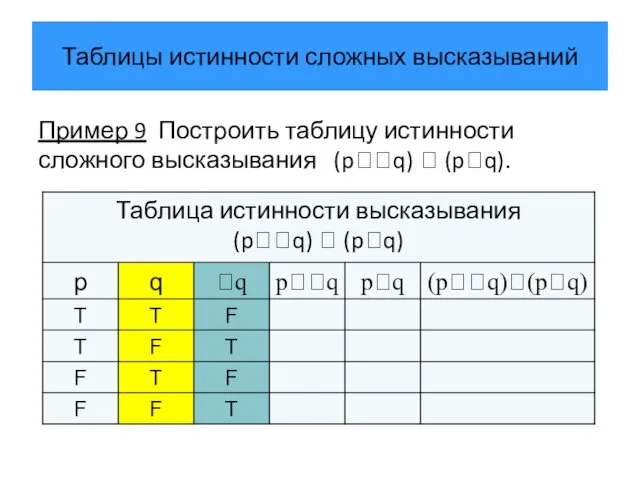
- 35. Таблицы истинности сложных высказываний Пример 9 Построить таблицу истинности сложного высказывания (pq) (pq).
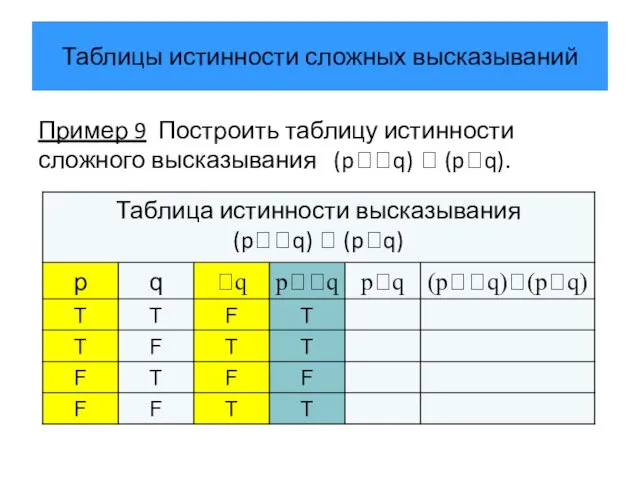
- 36. Таблицы истинности сложных высказываний Пример 9 Построить таблицу истинности сложного высказывания (pq) (pq).
- 37. Таблицы истинности сложных высказываний Пример 9 Построить таблицу истинности сложного высказывания (pq) (pq).
- 38. Таблицы истинности сложных высказываний Пример 9 Построить таблицу истинности сложного высказывания (pq) (pq).
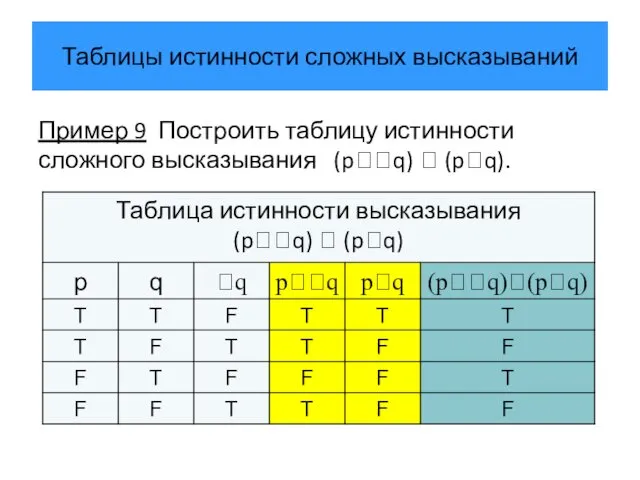
- 39. Таблицы истинности сложных высказываний Пример 9 Построить таблицу истинности сложного высказывания (pq) (pq).
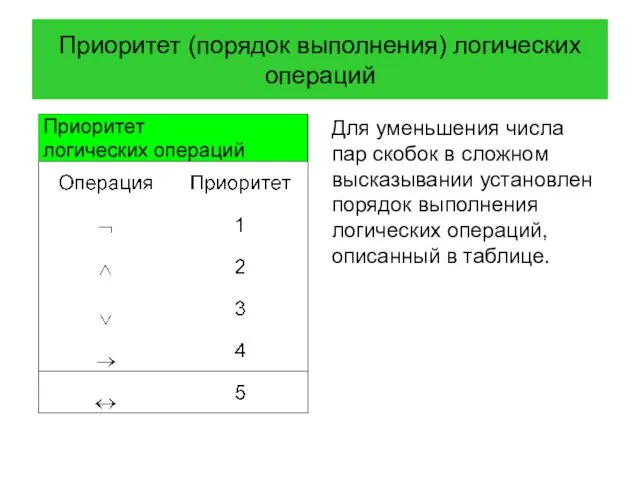
- 40. Приоритет (порядок выполнения) логических операций Для уменьшения числа пар скобок в сложном высказывании установлен порядок выполнения
- 41. Приоритет (порядок выполнения) логических операций Пример 10 Расставим скобки в сокращенной записи сложного высказывания p
- 42. Тавтологии и противоречия Определение 1 Сложное высказывание называется тавтологией, если оно истинно при любых истинностных значениях
- 43. Тавтологии и противоречия Определение 2 Сложное высказывание называется противоречием, если оно ложно при любых истинностных значениях
- 44. Тавтологии и противоречия Определение 3 Сложное высказывание называется контингенцией, если оно не является ни тавтологией ни
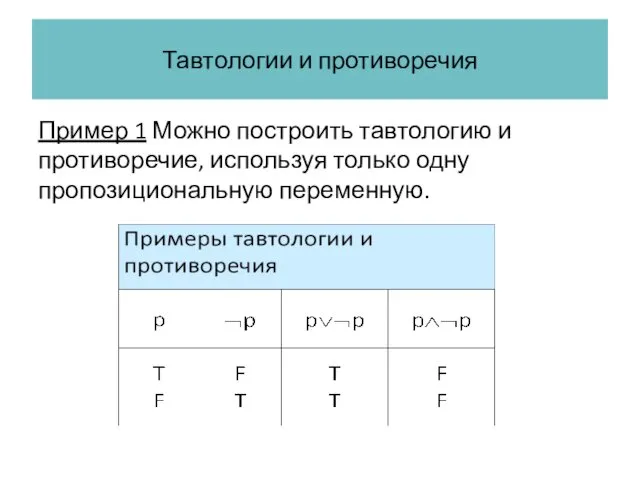
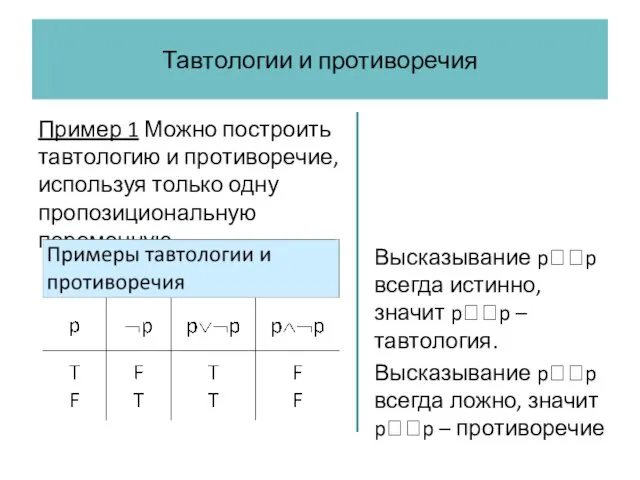
- 45. Тавтологии и противоречия Пример 1 Можно построить тавтологию и противоречие, используя только одну пропозициональную переменную.
- 46. Тавтологии и противоречия Пример 1 Можно построить тавтологию и противоречие, используя только одну пропозициональную переменную. Высказывание
- 47. Логическая эквивалентность высказываний Два сложных высказывания называются логически эквивалентными, если они имеют одинаковые истинностные значения на
- 48. Логическая эквивалентность высказываний Определение 4 Сложные высказывания p и q называются логически эквивалентными, если сложное высказывание
- 49. Логическая эквивалентность высказываний Для определения эквивалентности двух сложных высказываний можно использовать таблицы истинности. Будьте внимательны! В
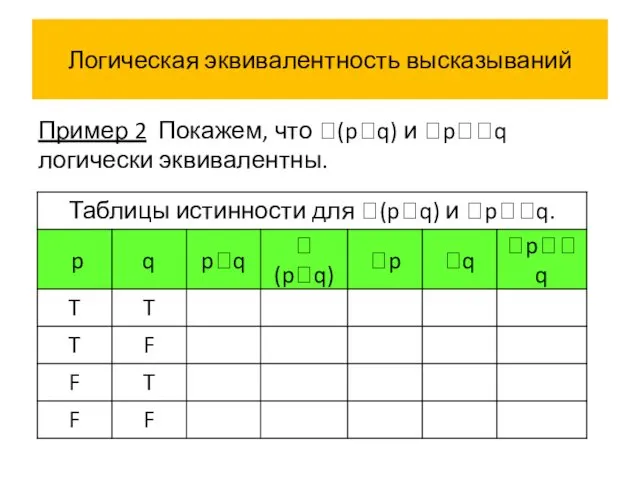
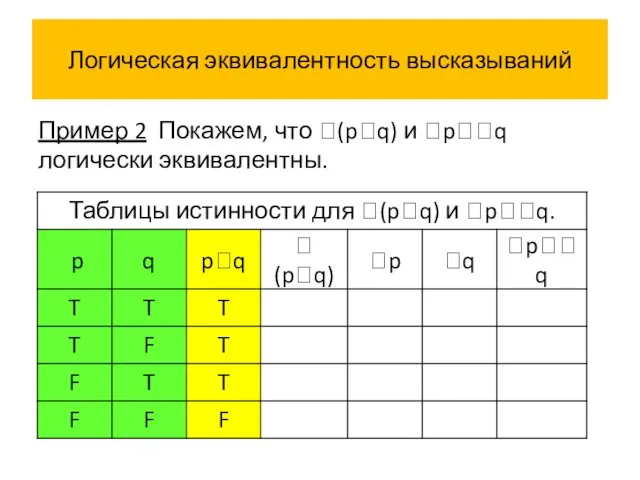
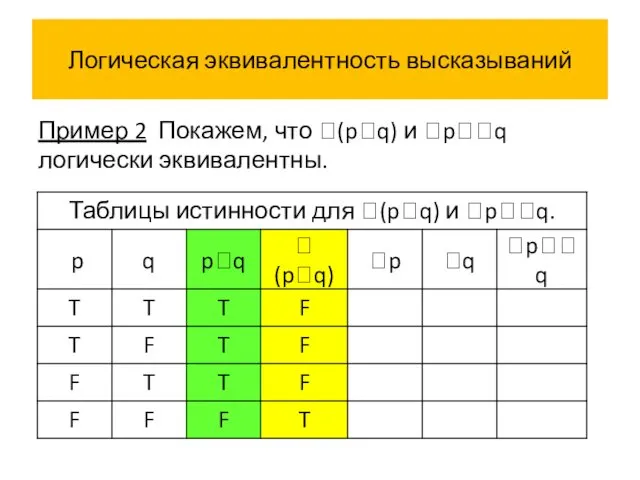
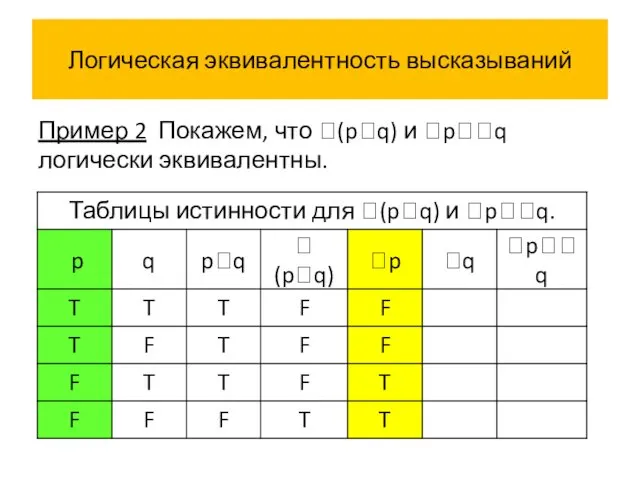
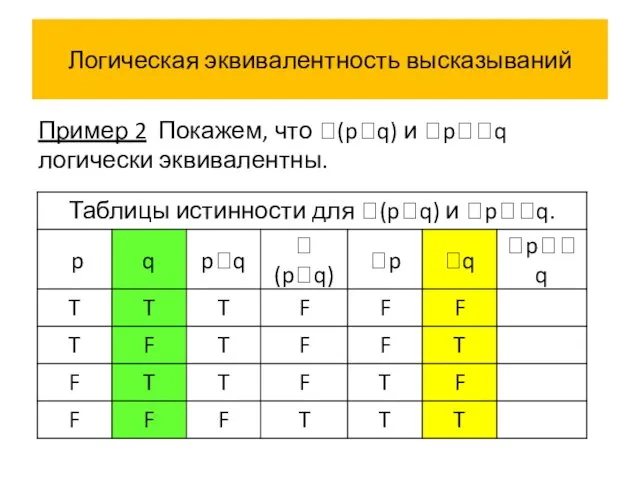
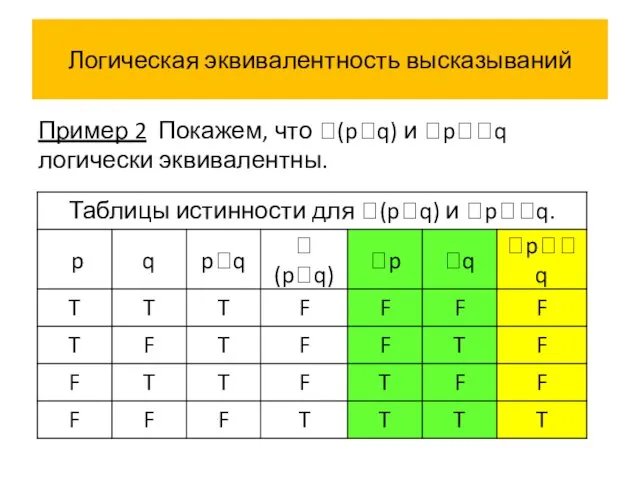
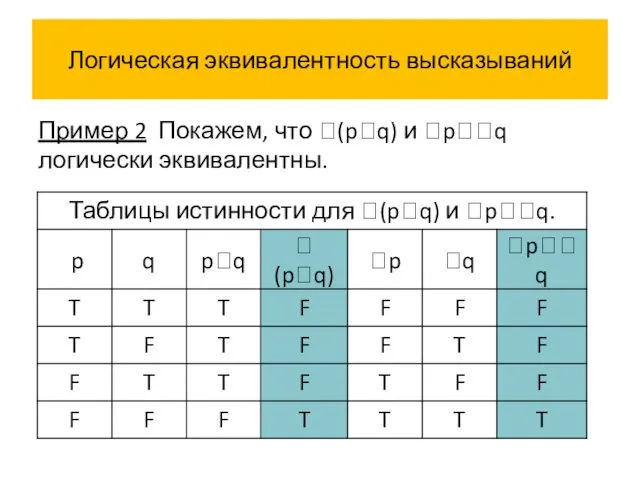
- 50. Логическая эквивалентность высказываний Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 51. Логическая эквивалентность высказываний Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 52. Логическая эквивалентность высказываний Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 53. Логическая эквивалентность высказываний Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 54. Логическая эквивалентность высказываний Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 55. Логическая эквивалентность высказываний Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 56. Логическая эквивалентность высказываний Пример 2 Покажем, что (pq) и pq логически эквивалентны.
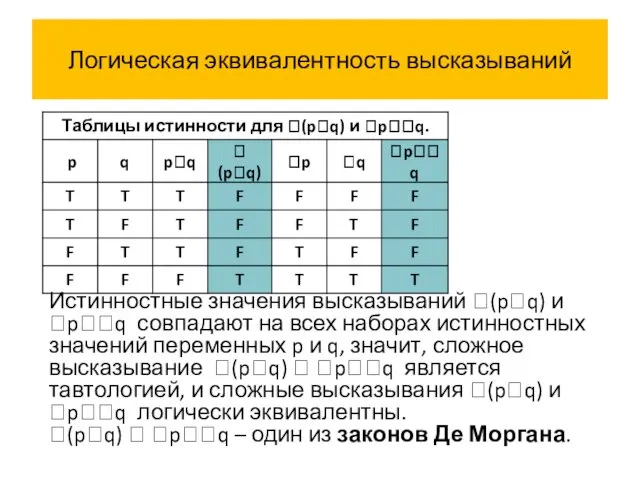
- 57. Логическая эквивалентность высказываний Истинностные значения высказываний (pq) и pq совпадают на всех наборах истинностных значений переменных
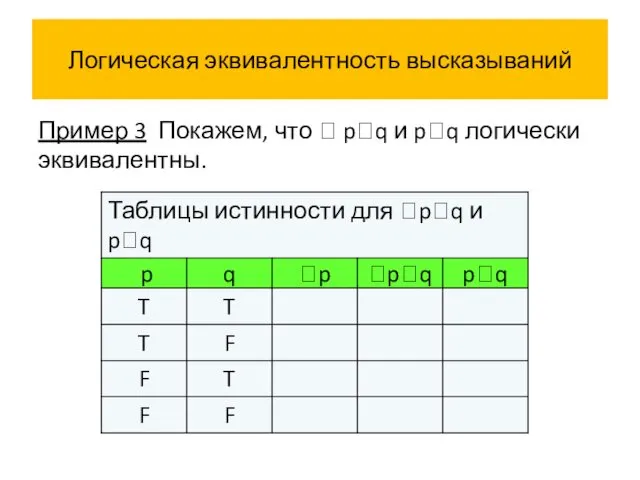
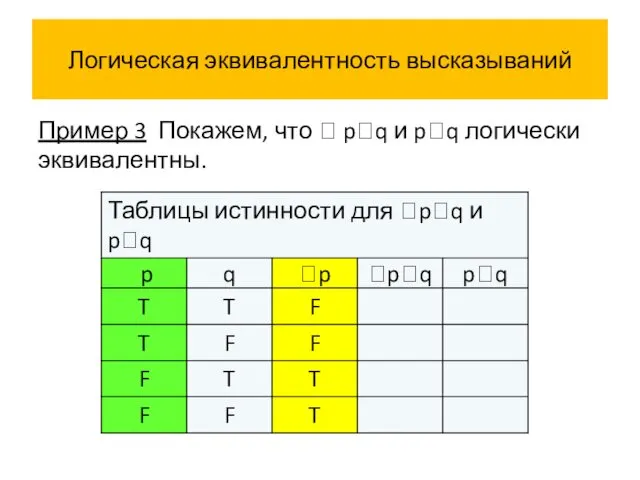
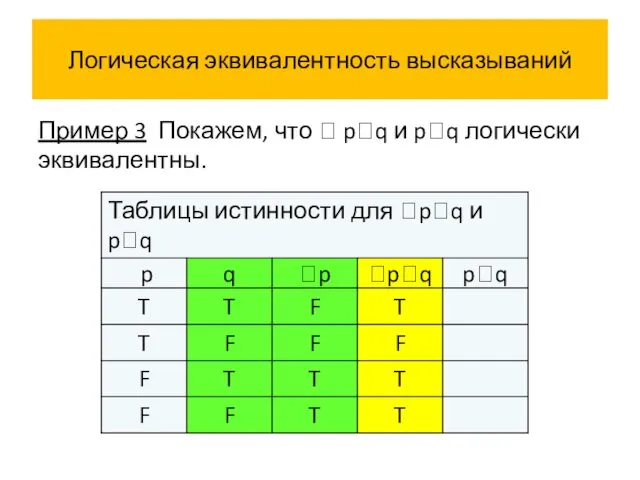
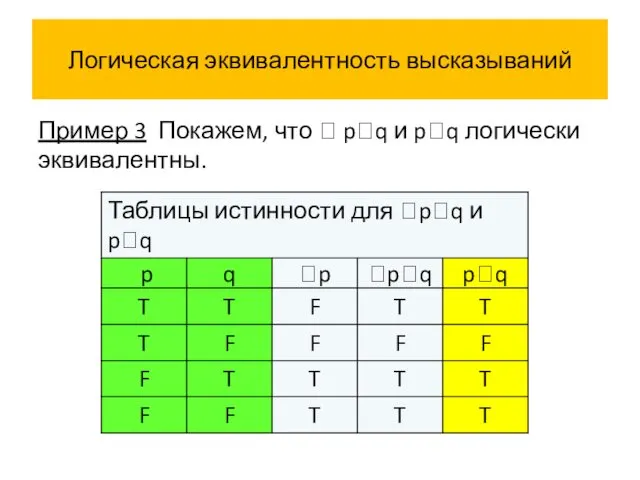
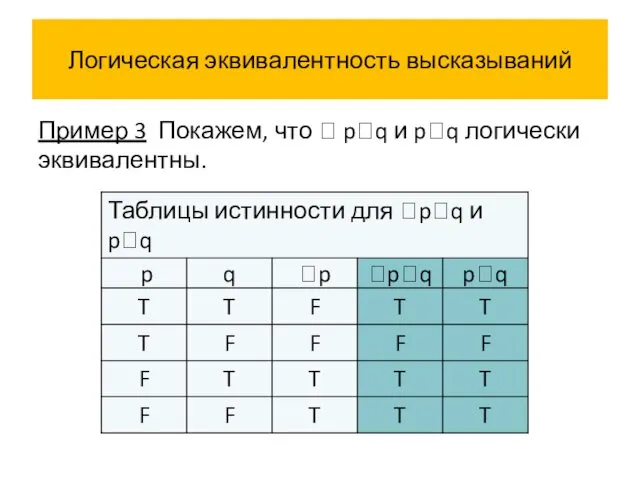
- 58. Логическая эквивалентность высказываний Пример 3 Покажем, что pq и pq логически эквивалентны.
- 59. Логическая эквивалентность высказываний Пример 3 Покажем, что pq и pq логически эквивалентны.
- 60. Логическая эквивалентность высказываний Пример 3 Покажем, что pq и pq логически эквивалентны.
- 61. Логическая эквивалентность высказываний Пример 3 Покажем, что pq и pq логически эквивалентны.
- 62. Логическая эквивалентность высказываний Пример 3 Покажем, что pq и pq логически эквивалентны.
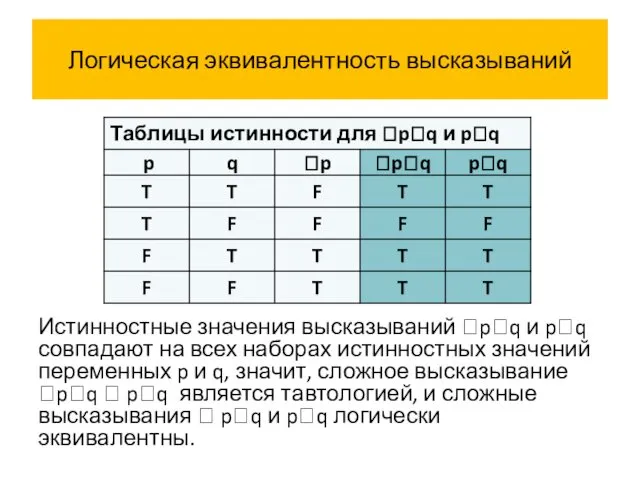
- 63. Логическая эквивалентность высказываний Истинностные значения высказываний pq и pq совпадают на всех наборах истинностных значений переменных
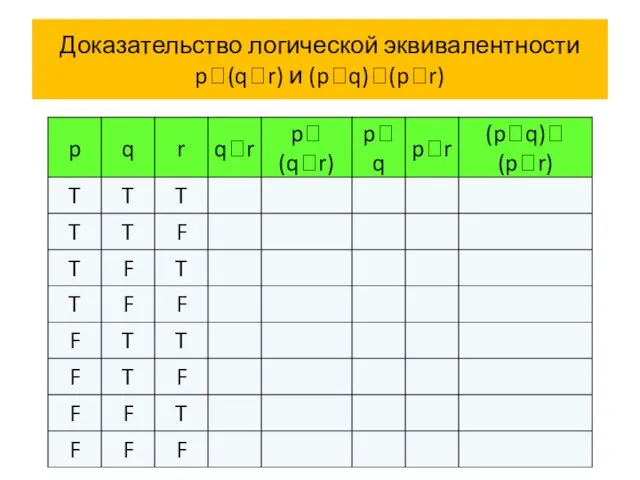
- 64. Логическая эквивалентность высказываний Пример 4 Покажем, что сложные высказывания p (q r) и (p
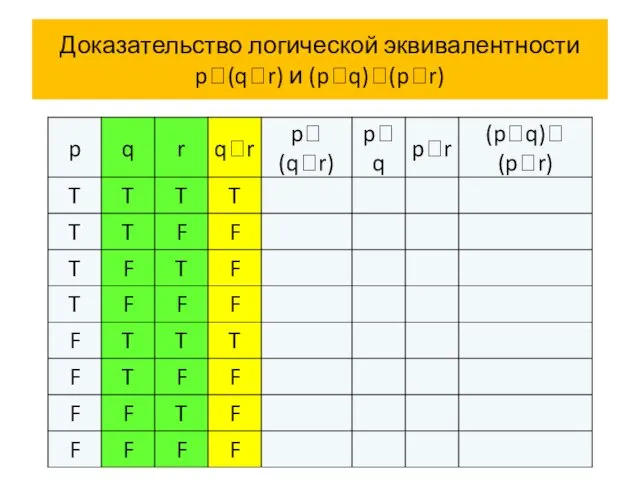
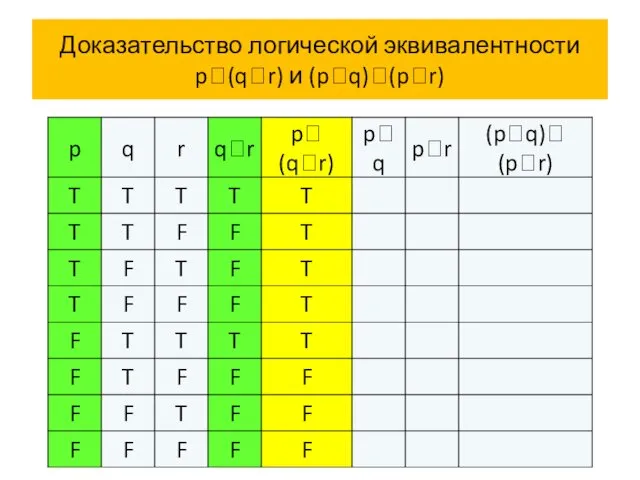
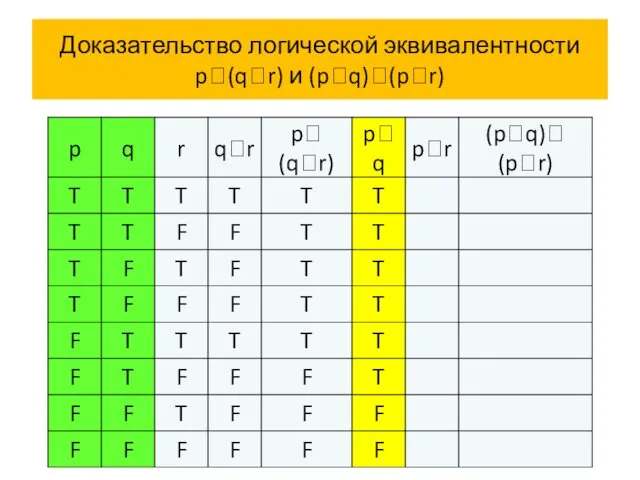
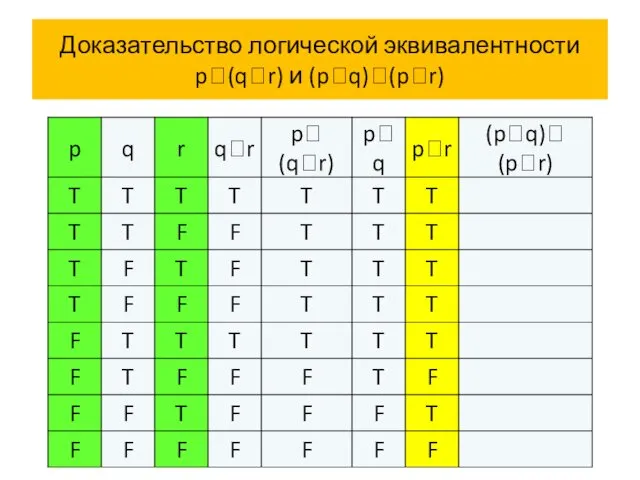
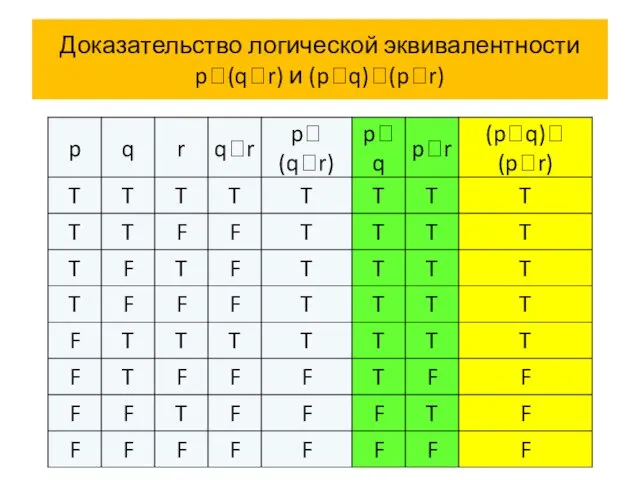
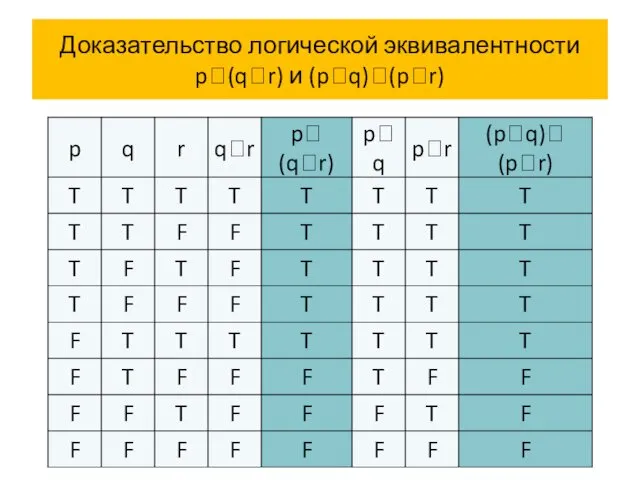
- 65. Доказательство логической эквивалентности p(qr) и (pq)(pr)
- 66. Доказательство логической эквивалентности p(qr) и (pq)(pr)
- 67. Доказательство логической эквивалентности p(qr) и (pq)(pr)
- 68. Доказательство логической эквивалентности p(qr) и (pq)(pr)
- 69. Доказательство логической эквивалентности p(qr) и (pq)(pr)
- 70. Доказательство логической эквивалентности p(qr) и (pq)(pr)
- 71. Доказательство логической эквивалентности p(qr) и (pq)(pr)
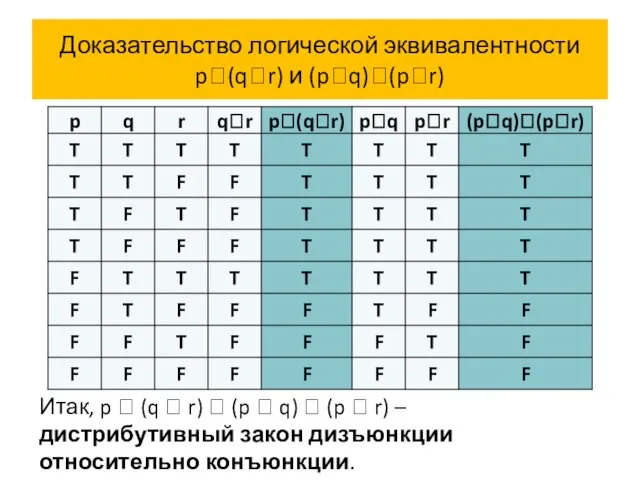
- 72. Доказательство логической эквивалентности p(qr) и (pq)(pr) Итак, p (q r) (p q)
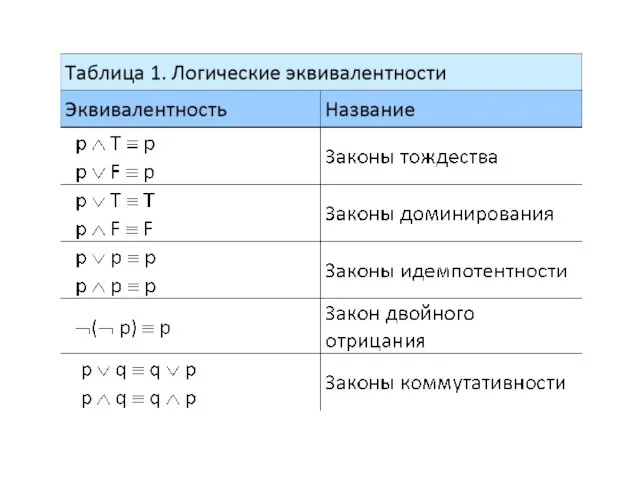
- 75. Логическая эквивалентность высказываний Множество сложных высказываний, на котором заданы логические операции , , , удовлетворяющие законам
- 78. Применение законов Де Моргана Пример 5 Используем закон Де Моргана для построения отрицания высказывания: «Сергей пойдет
- 79. Применение законов Де Моргана Пример 6 Используем закон Де Моргана для построения отрицания высказывания: «У Ольги
- 80. Построение новых логических эквивалентностей Логические эквивалентности таблиц 1, 2 и 3 можно использовать для построения новых
- 81. Построение новых логических эквивалентностей Пример 7 Покажем с помощью преобразований, что высказывания (p q) и
- 82. Построение новых логических эквивалентностей Пример 8 Покажем с помощью преобразований, что высказывания (p (p
- 83. Построение новых логических эквивалентностей Пример 9 Покажем с помощью преобразований, что высказывание (p q)
- 84. Выполнимые и невыполнимые высказывания Определение 5 Сложное высказывание называется выполнимым, если существует набор истинностных значений пропозициональных
- 85. Проблема выполнимости Определение 6 Набор истинностных значений пропозициональных переменных, на котором выполнимое высказывание принимает значение истина,
- 86. Выполнимые и невыполнимые высказывания Пример 9 Выясним, какие из следующих высказываний являются выполнимыми: (p q)
- 87. Проблема выполнимости В терминах выполнимости сложных высказываний моделируются задачи из различных областей науки и техники: робототехники,
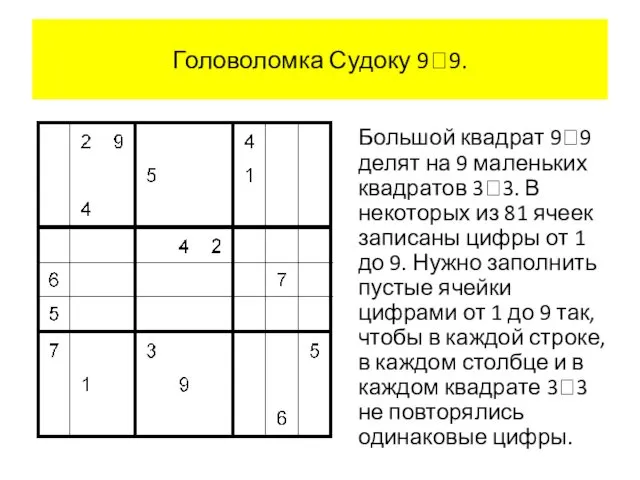
- 88. Головоломка Судоку 99. Большой квадрат 99 делят на 9 маленьких квадратов 33. В некоторых из 81
- 90. Скачать презентацию


















































 Комбинации многогранников и тел вращения
Комбинации многогранников и тел вращения Структура задачи
Структура задачи Векторы и их применение в прикладных науках
Векторы и их применение в прикладных науках Вопросы к экзамену
Вопросы к экзамену Скалярное произведение векторов. Угол между векторами
Скалярное произведение векторов. Угол между векторами Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Решение задач по теории вероятности (по материалам открытого банка задач ЕГЭ по математике)
Решение задач по теории вероятности (по материалам открытого банка задач ЕГЭ по математике) Решение задач на готовых чертежах. Подобные
Решение задач на готовых чертежах. Подобные Лабораторные работы 8 класс по геометрии Вписанная и описанная окружность
Лабораторные работы 8 класс по геометрии Вписанная и описанная окружность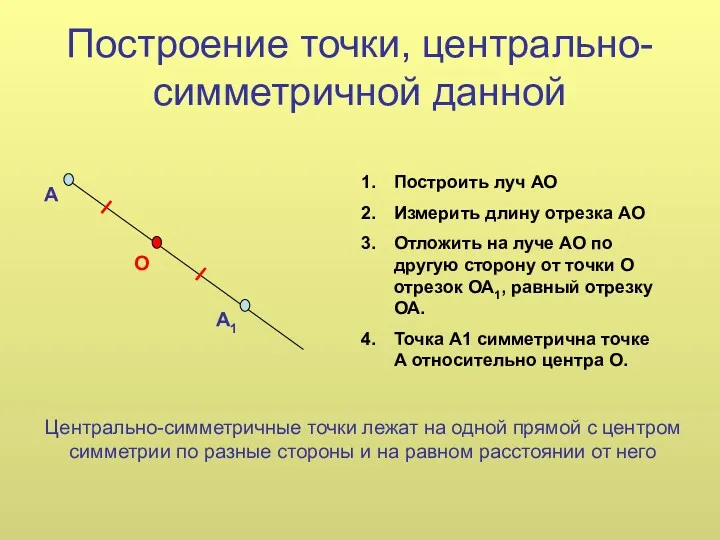 Построение точки, центрально-симметричной данной
Построение точки, центрально-симметричной данной Системы линейных уравнений
Системы линейных уравнений презентация урока по математике решение простых задач на нахождение остатка
презентация урока по математике решение простых задач на нахождение остатка Графики тригонометрических функций. Преобразования графиков функций
Графики тригонометрических функций. Преобразования графиков функций Из опыта работы по обучению детей с ограниченными возможностями здоровья по предмету Математика
Из опыта работы по обучению детей с ограниченными возможностями здоровья по предмету Математика Царстве математики. 6 класс
Царстве математики. 6 класс Столбчатые и линейные диаграммы
Столбчатые и линейные диаграммы Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Вычисление площадей с помощью интегралов
Вычисление площадей с помощью интегралов Презентация урока по математике Сложение дробей с одинаковыми знаменателями
Презентация урока по математике Сложение дробей с одинаковыми знаменателями Деление дробей
Деление дробей Понятие об исследовании операций
Понятие об исследовании операций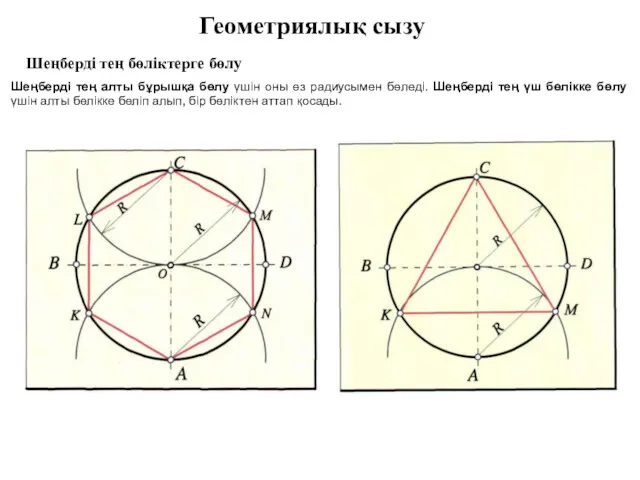 Геометриялық сызу
Геометриялық сызу Часть II. Случайные величины
Часть II. Случайные величины Дискретная математика. Теория множеств
Дискретная математика. Теория множеств Теорема Менелая
Теорема Менелая Решение задач с помощью кругов Эйлера
Решение задач с помощью кругов Эйлера Математические идеи в почвоведении. Методы статистического анализа данных. (Лекция 1)
Математические идеи в почвоведении. Методы статистического анализа данных. (Лекция 1) Умножение вектора на число
Умножение вектора на число