Содержание
- 2. План проекта: 1. Введение 2 2. История возникновения понятия вектор. 3 3. Применение векторов в прикладн
- 3. 1. Введение Данная работа посвящена рассмотрению векторного аппарата геометрии. С помощью векторов можно доказывать теоремы, решать
- 4. Гипотеза Векторы находят широкое применение в геометрии и в прикладных науках.
- 5. Задачи: 1. Провести исследования по данной теме. 2. Рассмотреть понятие «вектор» в предметах естественно-научного цикла. 3.
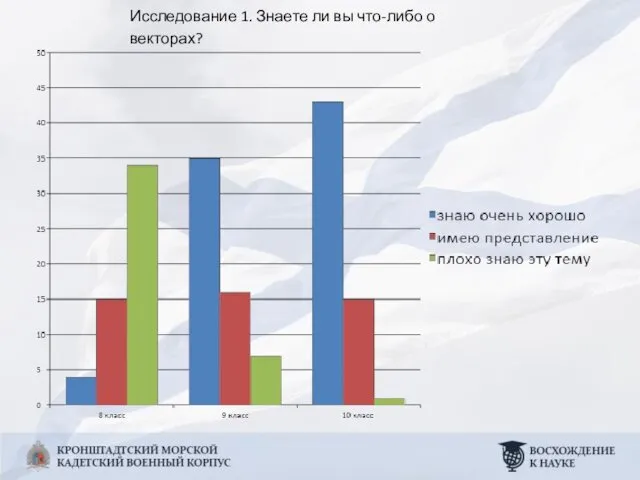
- 6. Исследование 1. Знаете ли вы что-либо о векторах?
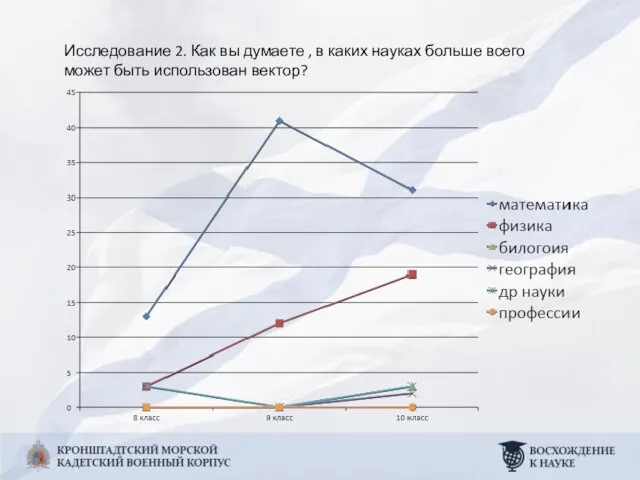
- 7. Исследование 2. Как вы думаете , в каких науках больше всего может быть использован вектор?
- 8. История возникновения понятия вектор. Вектор – молодое математическое понятие. Этот термин впервые употребил ирландский математик Уильям
- 9. В 1587 г. был опубликован на голландском языке трактат фламандского ученого С. Стевина (1548-1620) «Начала статики».
- 10. Начала исчисления направленных отрезков были впервые изложены норвежцем Каспаром Весселем в мемуаре «Опыт об аналитическом представлении
- 11. Система координат Р. Декарта основана на его концепции единой математики, объединяющей геометрию и алгебру. Развивая мысли
- 12. Лазар Николя Карно также внес свой вклад в векторное исчисление.До него положительные и отрицательные отрезки рассматривались
- 13. В конце 16- начале 17 в. многие ученые - физики, в том числе Леонардо да Винчи,
- 14. Галиле́о Галиле́й— итальянский физик, механик, астроном, философ, математик, оказавший значительное влияние на науку своего времени. Он
- 15. Иога́нн Ке́плер— немецкий математик, астроном, механик, оптик, первооткрыватель законов движения планет Солнечной системы.(использовал векторное направление)
- 16. В последней четверти 19 в. происходит слияние, синтез трех путей (геометрического, алгебраического и физического) исторического развития
- 17. Применение векторов в прикладных науках.
- 18. Векторы в географии Оказывается, векторы, как отрезки, показывающие направление нашли своё отражение и в географии. Так,
- 19. Мы можем увидеть природное явление- молния, которая как-никак, вектор
- 20. Векторы в физике Векторы — мощный инструмент не только математики, но и физики. Векторные величины в
- 21. Электрический ток- также является вектором
- 22. Векторы в навигации. Часто для навигации в 3D программисты берут единичные вектора и, путём умножения их
- 23. Векторы в экономике Векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической.
- 24. Векторы в психологии Все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует
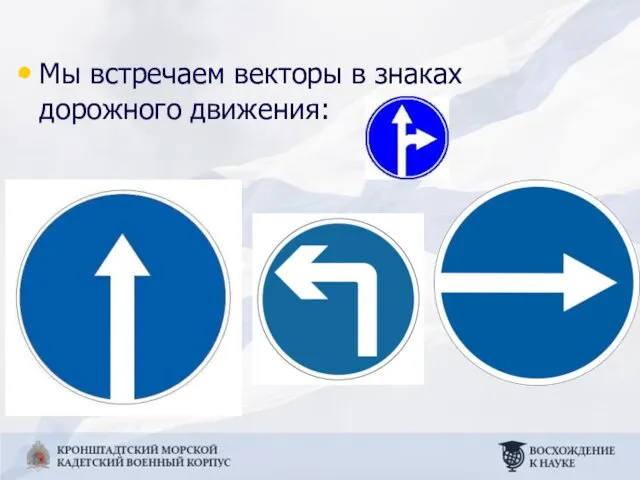
- 25. Мы встречаем векторы в знаках дорожного движения:
- 26. Векторы в профессиях Мы выяснили, что векторы используются во многих науках для моделирования самых различных процессов
- 27. Заключение Каждый человек постоянно сталкивается с векторами в повседневной жизни. Векторы необходимы нам для изучения не
- 29. Скачать презентацию






















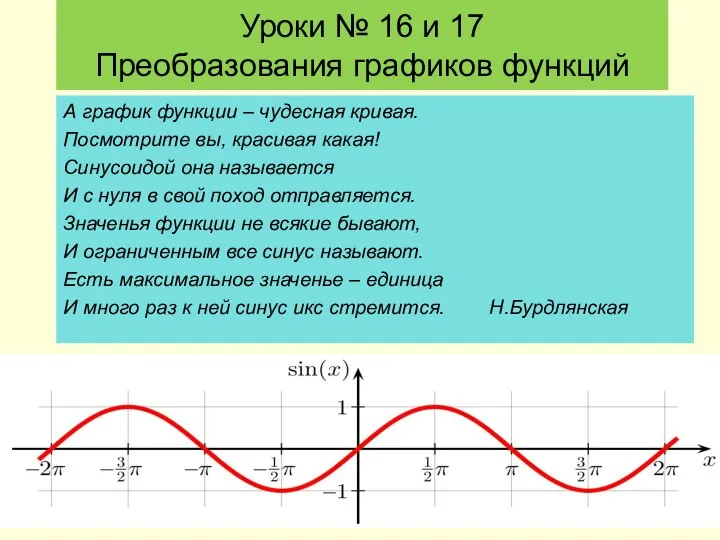 Преобразования графиков функций
Преобразования графиков функций Прогрессии вокруг нас
Прогрессии вокруг нас Математические методы и модели исследования операций. Этапы математического моделирования
Математические методы и модели исследования операций. Этапы математического моделирования Решение заданий ЕГЭ В6 (часть 1)
Решение заданий ЕГЭ В6 (часть 1) Арксинус, арккосинус, арктангенс и арккотангенс. Алгебра и начало анализа 10 класс
Арксинус, арккосинус, арктангенс и арккотангенс. Алгебра и начало анализа 10 класс Производная и ее применения
Производная и ее применения Большая математическая мастерская
Большая математическая мастерская Уравнение и его корни. Алгебра 7 класс
Уравнение и его корни. Алгебра 7 класс Объемы. Соотношения между единицами объема
Объемы. Соотношения между единицами объема Площадь круга и кругового сектора
Площадь круга и кругового сектора Произведение многочленов
Произведение многочленов Способы решения задачи
Способы решения задачи Соотношение между углами и сторонами треугольника
Соотношение между углами и сторонами треугольника Понятие положительной скалярной величины и ее измерения
Понятие положительной скалярной величины и ее измерения Элементы теории графов. Тема 2
Элементы теории графов. Тема 2 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Простые дроби
Простые дроби Нахождение расстояния между двумя точками на координатной прямой
Нахождение расстояния между двумя точками на координатной прямой Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы
Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы Тренажер по математике для учащихся 1 класса Приключение богатырей
Тренажер по математике для учащихся 1 класса Приключение богатырей Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов
Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов Интерактивный плакат Геометрические фигуры. 1-4 класс
Интерактивный плакат Геометрические фигуры. 1-4 класс Натуральные числа и шкалы
Натуральные числа и шкалы Vectors and the geometry of space
Vectors and the geometry of space Формирование знаний и умений вычисления периметра многоугольников.
Формирование знаний и умений вычисления периметра многоугольников. Название компонентов и результата действия деления. 2 класс
Название компонентов и результата действия деления. 2 класс Десятичные дроби. 5 класс
Десятичные дроби. 5 класс