Содержание
- 2. 1. ОПРЕДЕЛЕНИЕ И ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН СЛУЧАЙНОЙ НАЗЫВАЮТ ВЕЛИЧИНУ, КОТОРАЯ В РЕЗУЛЬТАТЕ ИСПЫТАНИЯ ПРИНИМАЕТ ОДНО ИЗ
- 3. Обозначение: Случайные величины – X, Y Их значения – x, y То, что случайная величина Х
- 4. ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН
- 5. Дискретная случайная величина (ДСВ) ДИСКРЕТНОЙ называется величина, принимающая отдельные, изолированные значения, которые можно перенумеровать (сосчитать). Примеры:
- 6. Непрерывная случайная величина (НСВ) НЕПРЕРЫВНОЙ называется величина, принимающая любые значения из некоторого интервала. Таких значений всегда
- 7. Примеры: Температура тела человека в норме (36,0 Артериальное давление.
- 8. 2. СПОСОБЫ ЗАДАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН Случайная величина задается ЗАКОНОМ РАСПРЕДЕЛЕНИЯ. ЗАКОН РАСПРЕДЕЛЕНИЯ – ВЗАИМОСВЯЗЬ МЕЖДУ ВОЗМОЖНЫМИ
- 9. РЯД РАСПРЕДЕЛЕНИЯ РЯД РАСПРЕДЕЛЕНИЯ: указываются все возможные значения хi ДСВ и их вероятности pi, обычно в
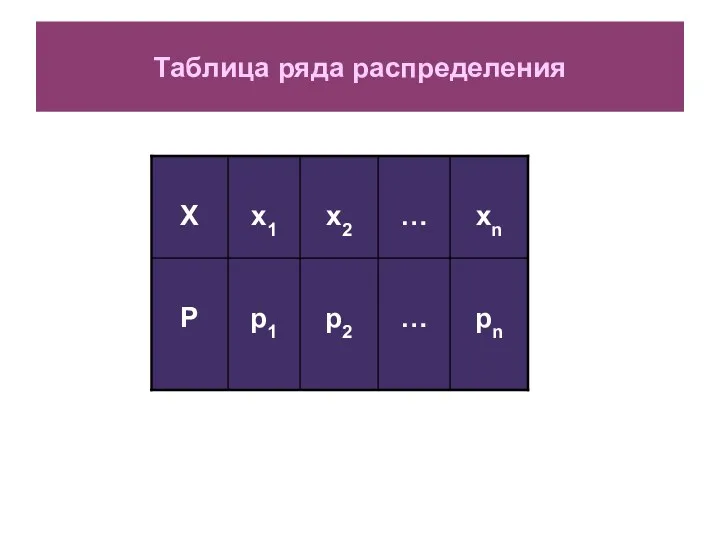
- 10. Таблица ряда распределения
- 11. УСЛОВИЕ НОРМИРОВКИ ДСВ СУММА ВЕРОЯТНОСТЕЙ ВСЕХ ЗНАЧЕНИЙ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ РАВНА ЕДИНИЦЕ,
- 12. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ: функция, значение которой при любом х равно вероятности того, что случайная величина
- 13. ПЛОТНОСТЬ ВЕРОЯТНОСТИ ПЛОТНОСТЬ ВЕРОЯТНОСТИ НСВ- производная функции распределения этой величины: f (x) = F ′ (x).
- 14. ВЕРОЯТНОСТНЫЙ СМЫСЛ ПЛОТНОСТИ ВЕРОЯТНОСТИ Чем больше плотность вероятности НСВ в данной точке х, тем больше вероятность
- 15. ВЕРОЯТНОСТЬ ПОПАДАНИЯ значений СВ В ПРОИЗВОЛЬНЫЙ ИНТЕРВАЛ Вероятность того, что любая случайная величина примет значения в
- 16. 3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СВ – ЭТО ЧИСЛА, КАЖДОЕ ИЗ КОТОРЫХ ХАРАКТЕРИЗУЕТ СЛУЧАЙНУЮ
- 17. Основные числовые характеристики ОСНОВНЫЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ: МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ М(Х) ДИСПЕРСИЯ D (X) СРЕДНЕКВАДРАТИ-ЧЕСКОЕ ОТКЛОНЕНИЕ σ (Х)
- 18. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ (ТЕОРЕТИЧЕСКОЕ СРЕДНЕЕ) СЛУЧАЙНОЙ ВЕЛИЧИНЫ ПРИБЛИЖЕННО РАВНО СРЕДНЕМУ АРИФМЕТИЧЕСКОМУ ВСЕХ НАБЛЮДАЕМЫХ ЗНАЧЕНИЙ ЭТОЙ
- 19. Формулы вычисления М(Х) МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ ДИСКРЕТНОЙ СВ Х называется число M (X) = =x1p1+ x2p2 +...+
- 20. ДИСПЕРСИЯ II. ДИСПЕРСИЯ ХАРАКТЕРИЗУЕТ СТЕПЕНЬ РАССЕЯНИЯ НАБЛЮДАЕМЫХ ЗНАЧЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ВОКРУГ ЕЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ.
- 21. ДИСПЕРСИЯ ОПРЕДЕЛЯЕТСЯ ЧЕРЕЗ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ: ЭТО ЧИСЛО, РАВНОЕ МАТЕМАТИЧЕСКОМУ ОЖИДАНИЮ КВАДРАТА ОТКЛОНЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ОТ ЕЕ
- 22. X2 БОЛЕЕ УДОБНАЯ ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ: D (X) = M (X2) – M2 (X). Если ДСВ
- 23. Размерность числовых характеристик РАЗМЕРНОСТЬ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ – КАК У САМОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. РАЗМЕРНОСТЬ ДИСПЕРСИИ РАВНА КВАДРАТУ
- 24. СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ III. СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ - ЭТО ЧИСЛО σ(X) = √ D (X). Отcюда D(X) =
- 25. Как и дисперсия, среднеквадратическое отклонение характеризует степень рассеяния наблюдаемых значений случайной величины вокруг ее математического ожидания.
- 27. Скачать презентацию






















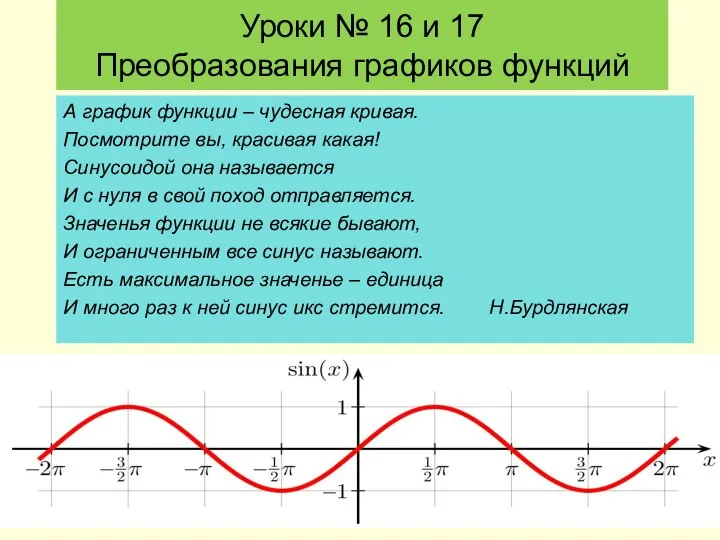 Преобразования графиков функций
Преобразования графиков функций Прогрессии вокруг нас
Прогрессии вокруг нас Математические методы и модели исследования операций. Этапы математического моделирования
Математические методы и модели исследования операций. Этапы математического моделирования Решение заданий ЕГЭ В6 (часть 1)
Решение заданий ЕГЭ В6 (часть 1) Арксинус, арккосинус, арктангенс и арккотангенс. Алгебра и начало анализа 10 класс
Арксинус, арккосинус, арктангенс и арккотангенс. Алгебра и начало анализа 10 класс Производная и ее применения
Производная и ее применения Большая математическая мастерская
Большая математическая мастерская Уравнение и его корни. Алгебра 7 класс
Уравнение и его корни. Алгебра 7 класс Объемы. Соотношения между единицами объема
Объемы. Соотношения между единицами объема Площадь круга и кругового сектора
Площадь круга и кругового сектора Произведение многочленов
Произведение многочленов Способы решения задачи
Способы решения задачи Соотношение между углами и сторонами треугольника
Соотношение между углами и сторонами треугольника Понятие положительной скалярной величины и ее измерения
Понятие положительной скалярной величины и ее измерения Элементы теории графов. Тема 2
Элементы теории графов. Тема 2 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Простые дроби
Простые дроби Нахождение расстояния между двумя точками на координатной прямой
Нахождение расстояния между двумя точками на координатной прямой Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы
Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы Тренажер по математике для учащихся 1 класса Приключение богатырей
Тренажер по математике для учащихся 1 класса Приключение богатырей Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов
Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов Интерактивный плакат Геометрические фигуры. 1-4 класс
Интерактивный плакат Геометрические фигуры. 1-4 класс Натуральные числа и шкалы
Натуральные числа и шкалы Vectors and the geometry of space
Vectors and the geometry of space Формирование знаний и умений вычисления периметра многоугольников.
Формирование знаний и умений вычисления периметра многоугольников. Название компонентов и результата действия деления. 2 класс
Название компонентов и результата действия деления. 2 класс Десятичные дроби. 5 класс
Десятичные дроби. 5 класс