Содержание
- 2. Теория множеств Множества Операции над множествами Упорядоченные множества Соответствия Отображения и функции Отношения
- 3. Множества. Основные понятия Множество - совокупность определенных, вполне различаемых объектов, рассматриваемых как целое. Элемент множества -
- 4. Способы задания множеств Перечисление элементов М = {a1, a2, a3, …, ak} M9 = {1, 2,
- 5. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Глава 1. Теория множеств 1.1. Множество и его
- 6. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Обозначения и понятия «наивной» теории множеств. a ∈
- 7. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Операции над множествами. A ∪ B Объединение множеств
- 8. Объединение Объединением множеств А и В называется множество, состоящее из всех тех и только тех элементов,
- 9. Объединение N множеств Операция объединения может быть распространена на N множеств. Тогда записывают:
- 10. Пример операции объединения ПРИМЕР 1: {1,2,3} {2,3,4}= {1,2,3,4} ПРИМЕР 2: А – множество компонентов резисторов, В
- 11. Следствие операции объединения
- 12. Объединение N множеств Операция объединения может быть распространена на N множеств. Тогда записывают:
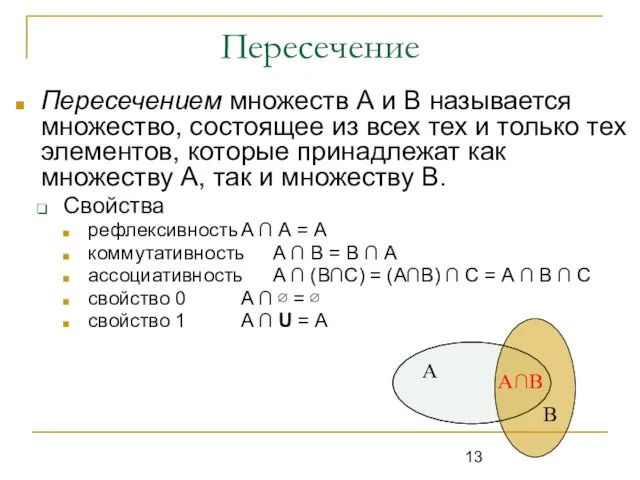
- 13. Пересечение Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов,
- 14. Операция пересечения или умножения ОПРЕДЕЛЕНИЕ: если даны два множества А и В, то пересечением их будет
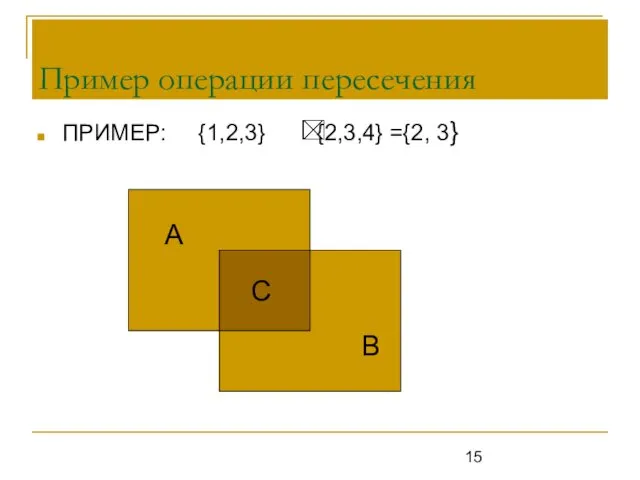
- 15. Пример операции пересечения ПРИМЕР: {1,2,3} {2,3,4} ={2, 3} А В С
- 16. СЛЕДСТВИЯ операции пересечения Для некоторой пары множеств может оказаться, что их пересечение равно пустому множеству. НАПРИМЕР
- 17. Непересекающиеся множества Множества, пересечение которых, является пустым множеством называются непересекающимися. ПРИМЕР 1: А – множество целых
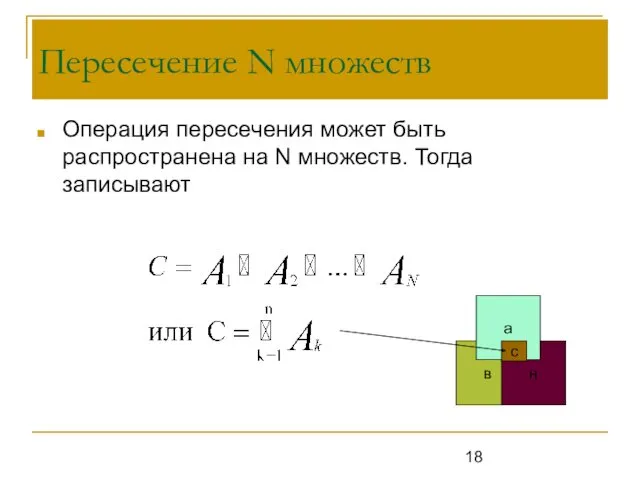
- 18. Пересечение N множеств Операция пересечения может быть распространена на N множеств. Тогда записывают в н а
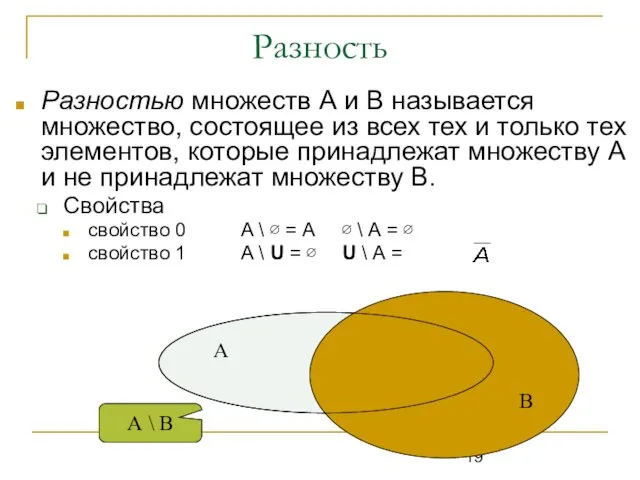
- 19. Разность Разностью множеств А и В называется множество, состоящее из всех тех и только тех элементов,
- 20. Вычитание множеств ОПРЕДЕЛЕНИЕ: Разностью множеств А и В называется совокупность тех элементов множества А, которые не
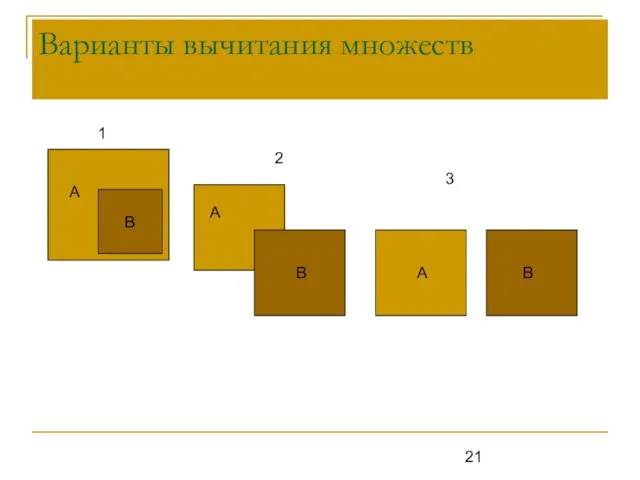
- 21. Варианты вычитания множеств А В А В А В 1 2 3
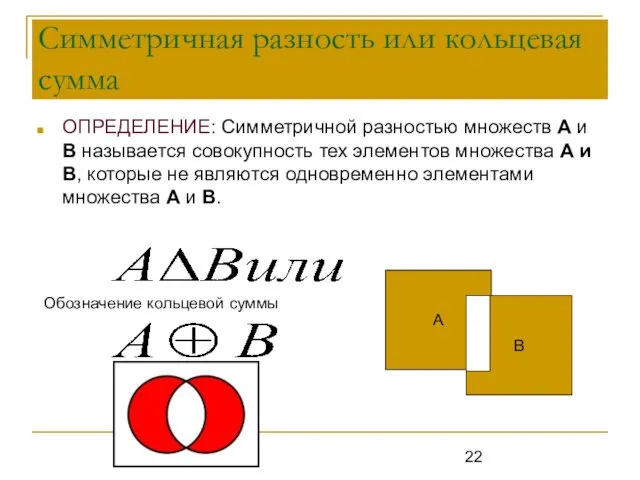
- 22. Симметричная разность или кольцевая сумма ОПРЕДЕЛЕНИЕ: Симметричной разностью множеств А и В называется совокупность тех элементов
- 23. Симметрическая разность Симметрической разностью множеств А и В называется множество, состоящее из всех тех и только
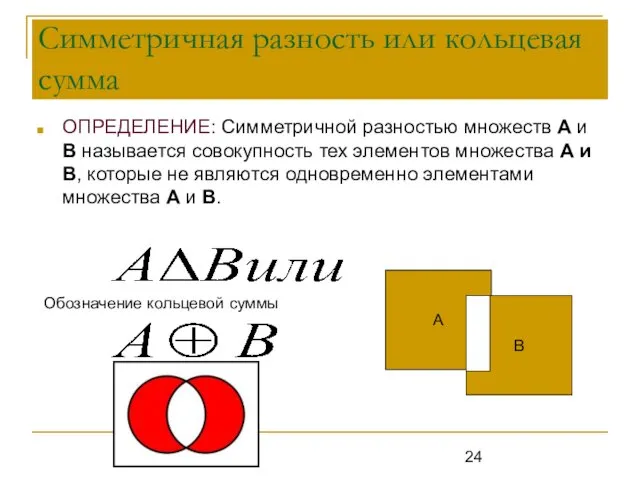
- 24. Симметричная разность или кольцевая сумма ОПРЕДЕЛЕНИЕ: Симметричной разностью множеств А и В называется совокупность тех элементов
- 25. Дополнение Дополнением множества А до универсального множества называется множество, состоящее из всех тех и только тех
- 26. Сравнение множеств Два множества равны между собой, если они состоят из одних и тех же элементов
- 27. Границы множества Если множество конечно и состоит из элементов, сравнимых между собой, то существуют наибольший и
- 28. Теорема о границах Если В⊆А, то inf В ≥ inf А; sup В ≤ sup А.
- 29. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Мощность множеств. Сравнение мощностей. Два множества называются равномощными,
- 30. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Сравнение мощностей. Часто можно определить, что два множества
- 32. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Сравнение мощностей (продолжение). Определение: Мощность множества всех вещественных
- 33. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Сравнение мощностей (продолжение). Теорема (без доказательства): пусть A'
- 34. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Сравнение мощностей (продолжение). Аналогично, (континуум) + (счетное) =
- 35. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Теорема Кантора. Для каждого множества A можно рассмотреть
- 36. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Доказательство теоремы Кантора Теорема (Г.Кантор): если множество A
- 37. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Доказательство теоремы Кантора (продолжение) Доказательство проводится по той
- 38. Кубенский А.А. Дискретная математика. Глава 1. Теория множеств. Некоторые следствия теоремы Кантора Поскольку 2N = C,
- 40. Скачать презентацию






























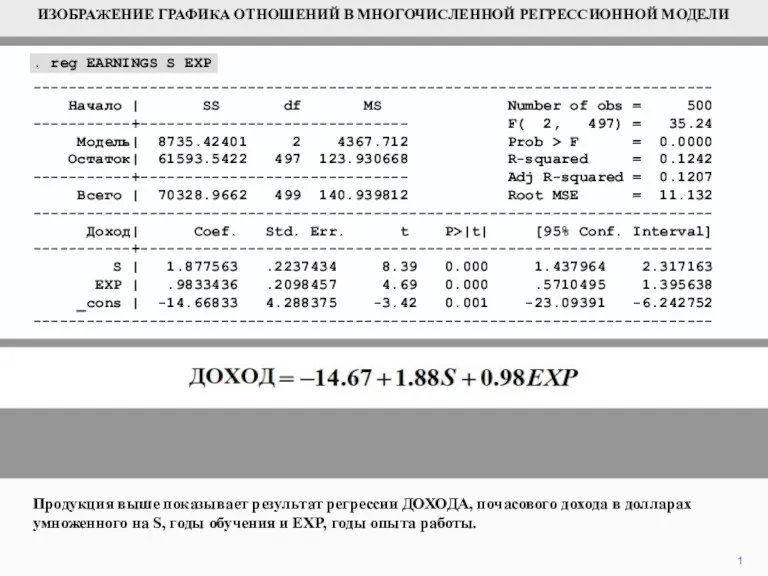 Изображение графика отношений в многочисленной регрессионной модели
Изображение графика отношений в многочисленной регрессионной модели Последовательность. Лингво–математический урок
Последовательность. Лингво–математический урок Подготовка учащихся к ОГЭ по математике
Подготовка учащихся к ОГЭ по математике Цилиндр, конус и шар
Цилиндр, конус и шар Движение по окружности
Движение по окружности Сумма углов треугольника
Сумма углов треугольника ГИА - 2012. Открытый банк заданий по математике. (Задача 4)
ГИА - 2012. Открытый банк заданий по математике. (Задача 4) Создание тренажера по подготовке к ОГЭ по математике
Создание тренажера по подготовке к ОГЭ по математике Центральные и вписанные углы
Центральные и вписанные углы Правильные многогранники
Правильные многогранники Элективный курс. Фигурные числа. (5-7 класс)
Элективный курс. Фигурные числа. (5-7 класс) Число и цифра 7.
Число и цифра 7. Активизация познавательной деятельности учащихся на уроках математики
Активизация познавательной деятельности учащихся на уроках математики Степени и корни
Степени и корни Полуплоскость. Луч. Прямая
Полуплоскость. Луч. Прямая Два замечательных предела
Два замечательных предела Рациональные неравенства. Задания для устного счета
Рациональные неравенства. Задания для устного счета Длина окружности (6 класс)
Длина окружности (6 класс)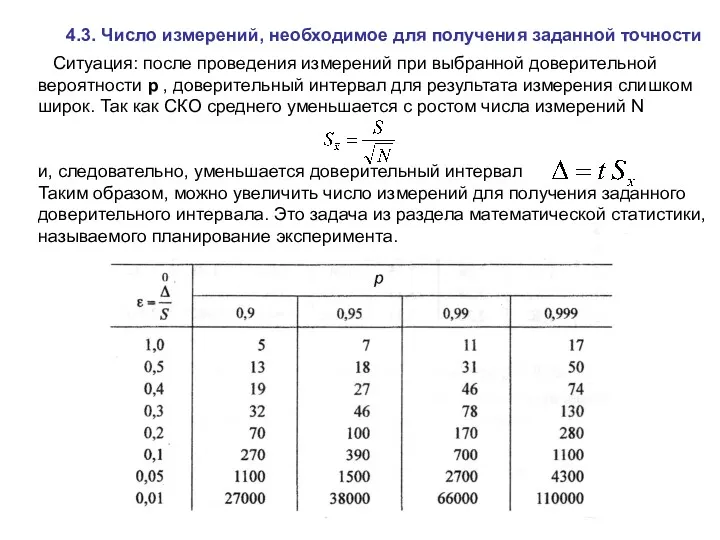 Число измерений, необходимое для получения заданной точности
Число измерений, необходимое для получения заданной точности Математическая игра Звездный час
Математическая игра Звездный час Основы математики
Основы математики The circle, the circumference and their elements. The central angle
The circle, the circumference and their elements. The central angle Положительные и отрицательные числа вокруг нас
Положительные и отрицательные числа вокруг нас Движение. Урок математики в 4 классе
Движение. Урок математики в 4 классе Обобщение по теме Четырехугольники. 8 класс
Обобщение по теме Четырехугольники. 8 класс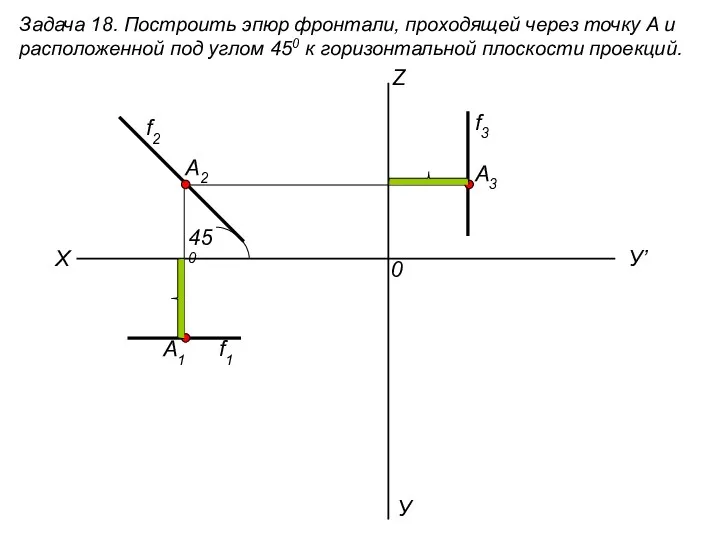 Построить эпюр фронтали, проходящей через точку А и расположенной под углом 450 к горизонтальной плоскости проекций. (задача 18)
Построить эпюр фронтали, проходящей через точку А и расположенной под углом 450 к горизонтальной плоскости проекций. (задача 18) методическая разработка урока математики Единицы времени.Век
методическая разработка урока математики Единицы времени.Век Статистические методы проверки гипотез
Статистические методы проверки гипотез