Содержание
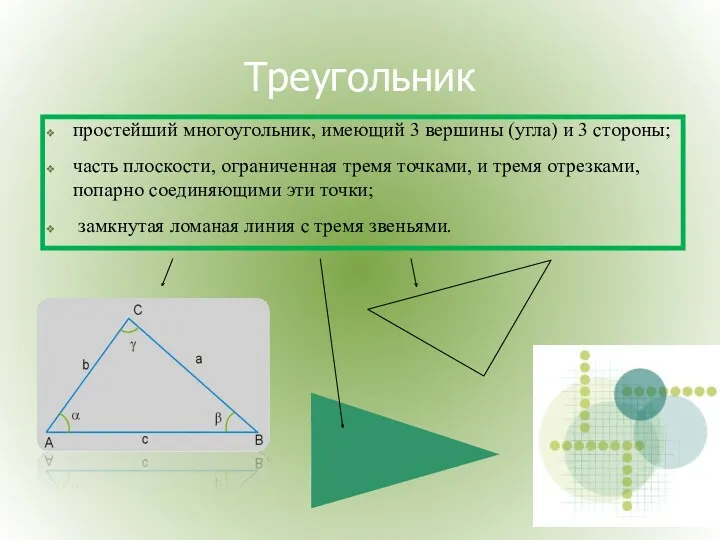
- 2. простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя
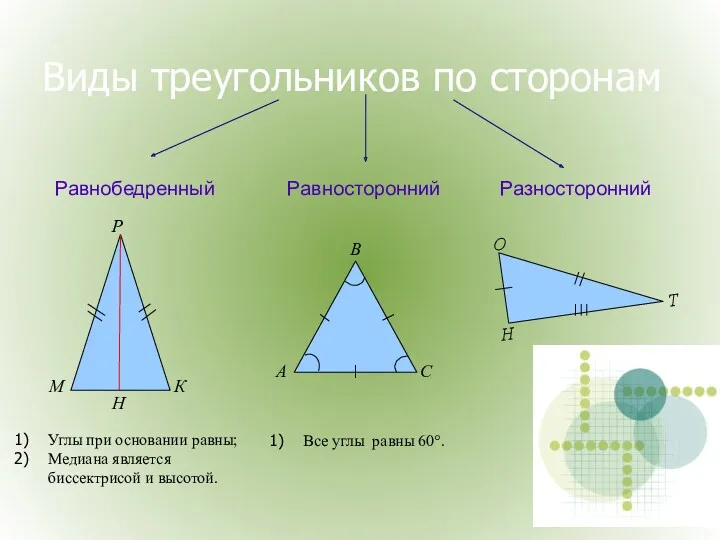
- 3. Виды треугольников по сторонам Равносторонний Равнобедренный Разносторонний Углы при основании равны; Медиана является биссектрисой и высотой.
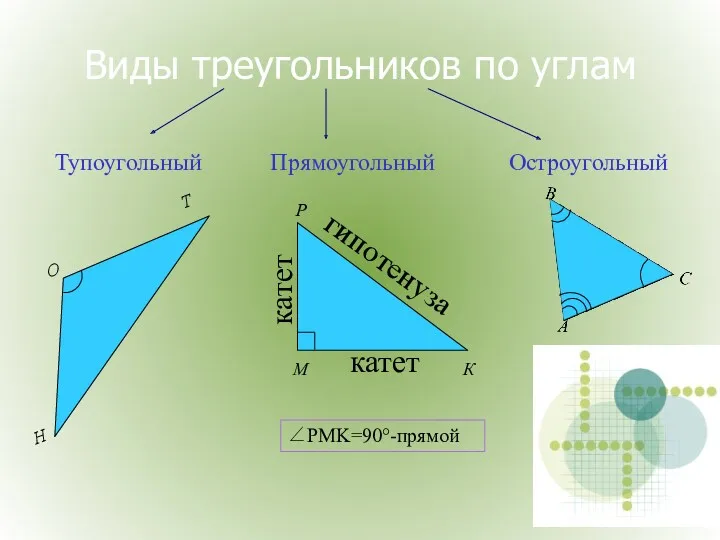
- 4. Виды треугольников по углам Прямоугольный Тупоугольный Н О Т Остроугольный катет катет гипотенуза ∠PMK=90°-прямой
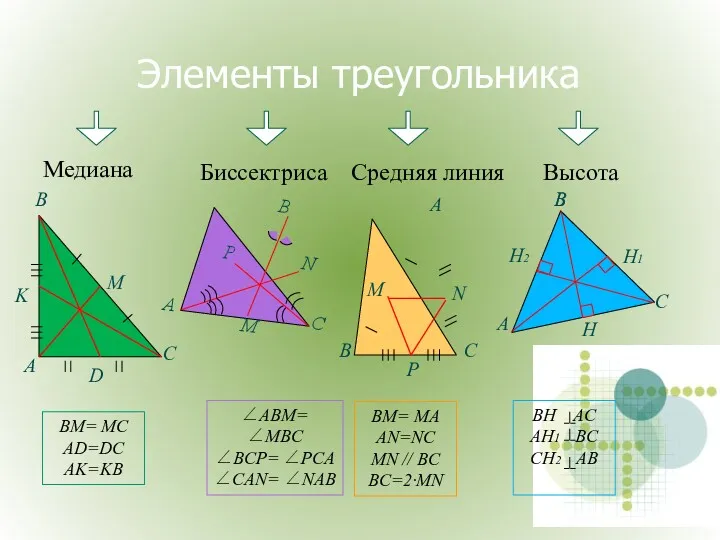
- 5. Элементы треугольника Медиана Высота Биссектриса Средняя линия BM= MC AD=DC AK=KB BM= MA AN=NC MN //
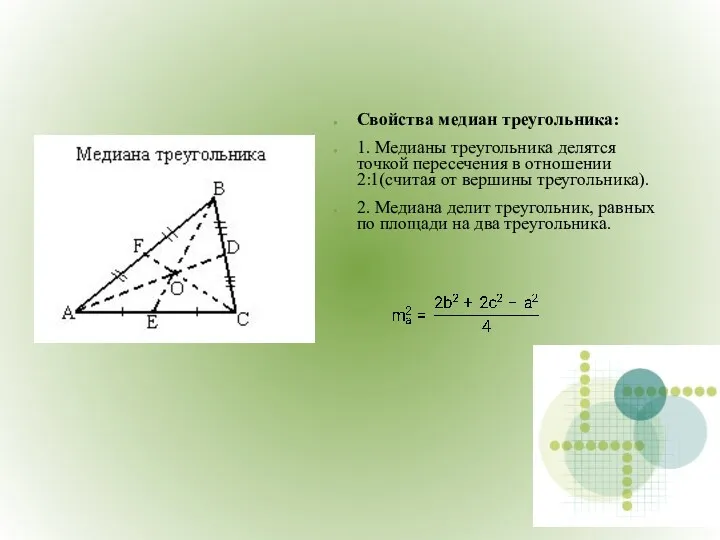
- 6. Свойства медиан треугольника: 1. Медианы треугольника делятся точкой пересечения в отношении 2:1(считая от вершины треугольника). 2.
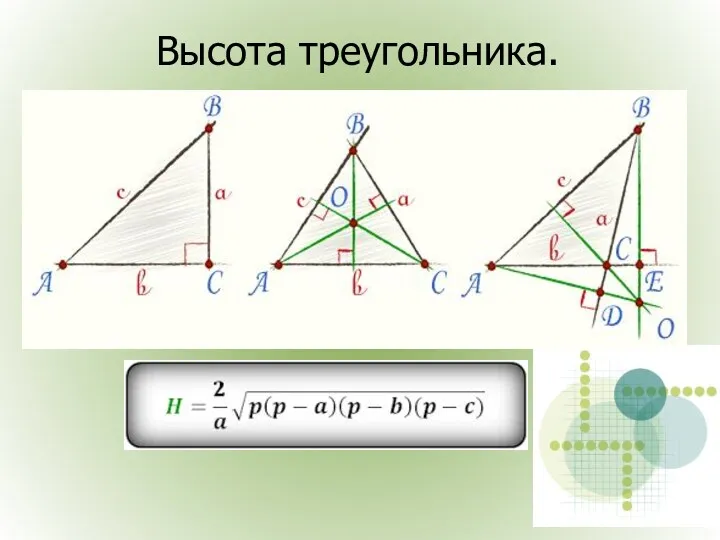
- 7. Высота треугольника.
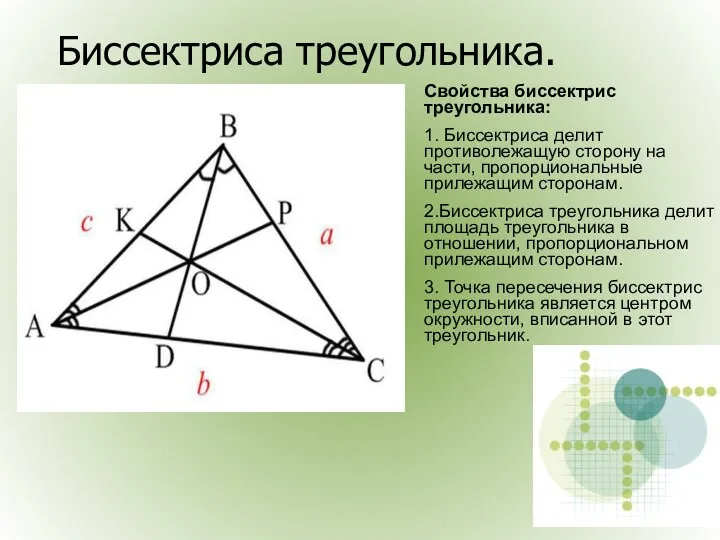
- 8. Биссектриса треугольника. Свойства биссектрис треугольника: 1. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. 2.Биссектриса
- 9. Средняя линия Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Свойство средней линии треугольника
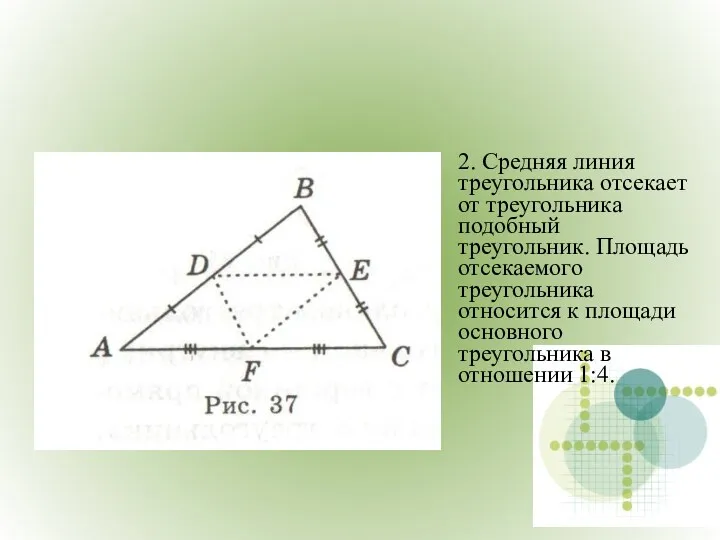
- 10. 2. Средняя линия треугольника отсекает от треугольника подобный треугольник. Площадь отсекаемого треугольника относится к площади основного
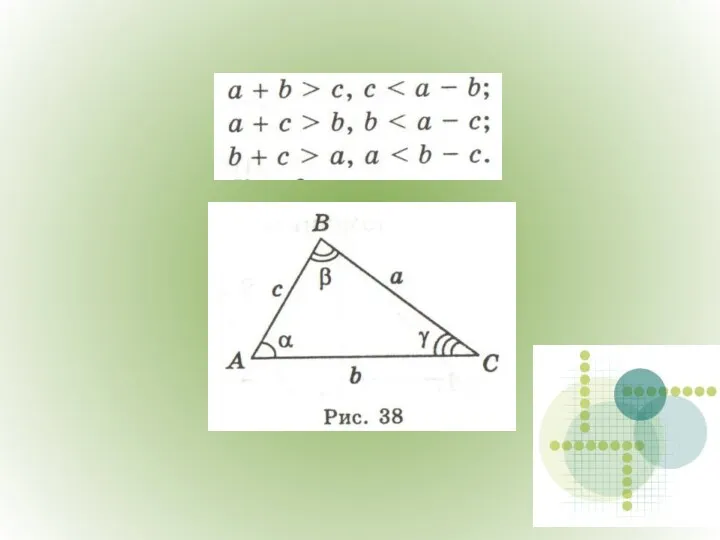
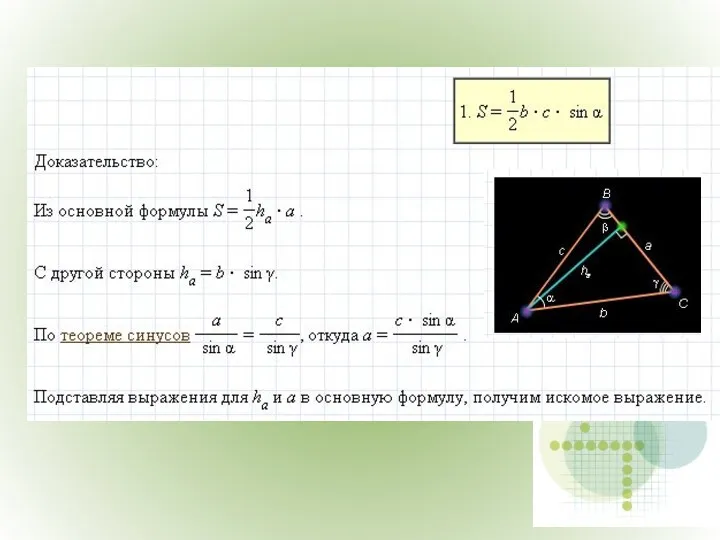
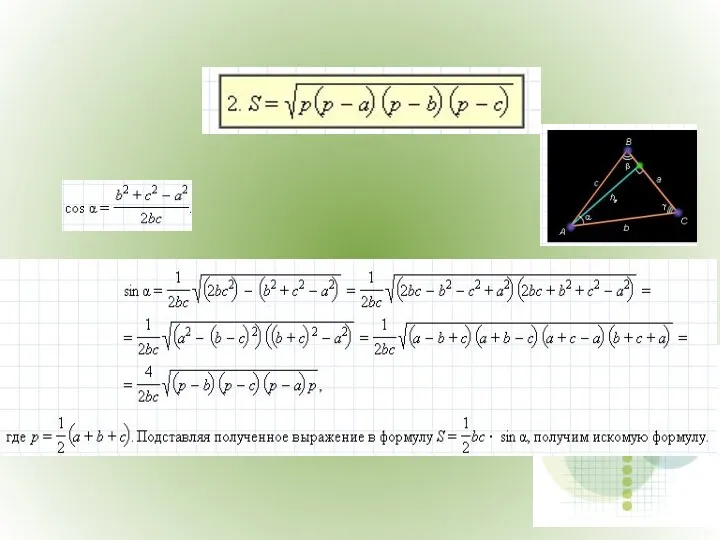
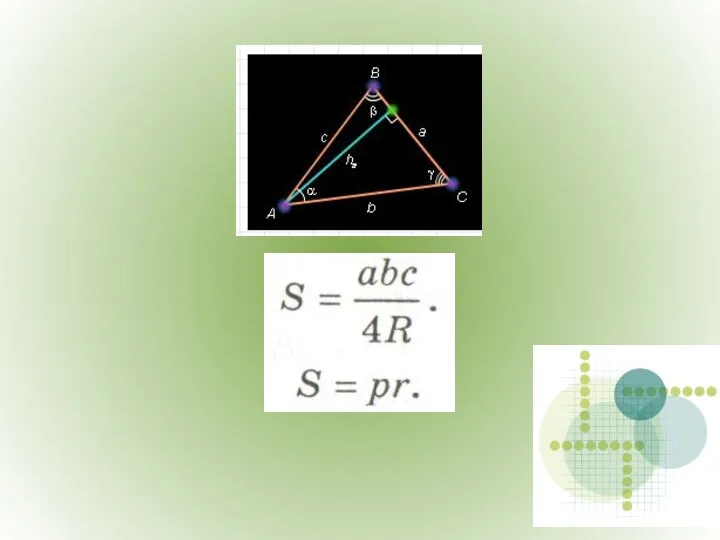
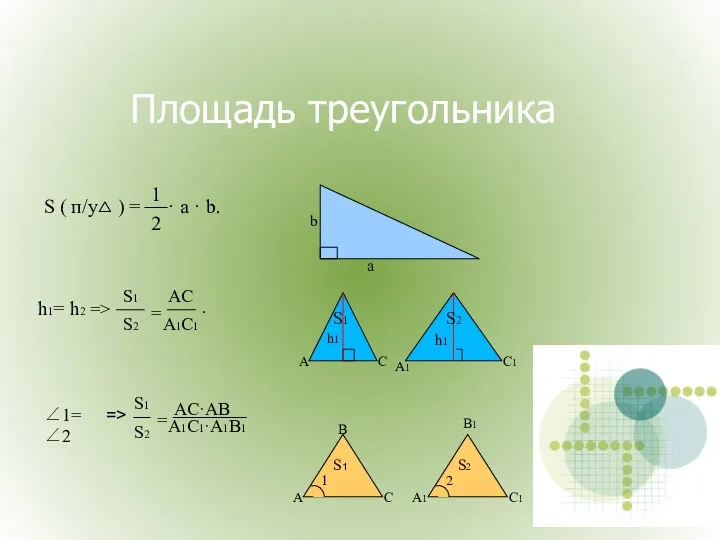
- 12. Площадь треугольника.
- 16. Площадь треугольника
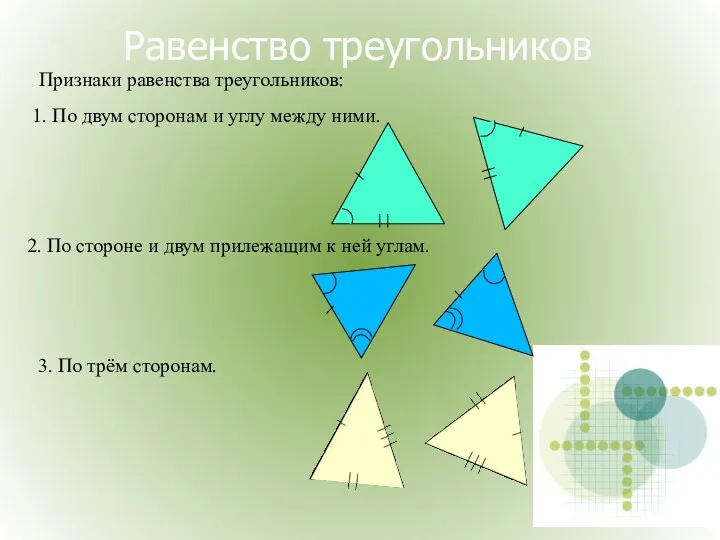
- 17. Равенство треугольников Признаки равенства треугольников: 2. По стороне и двум прилежащим к ней углам. 3. По
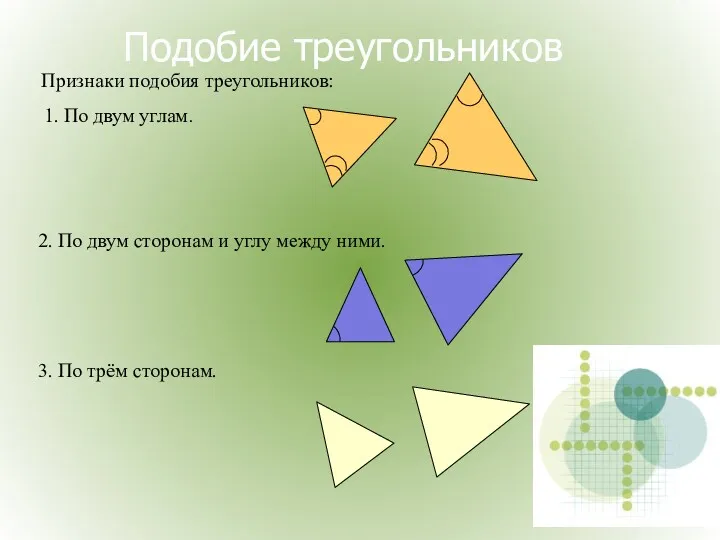
- 18. Подобие треугольников Признаки подобия треугольников: 1. По двум углам. 2. По двум сторонам и углу между
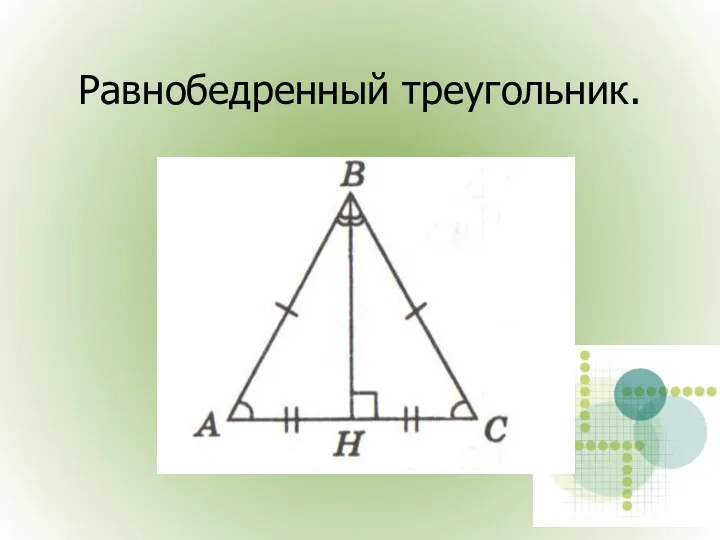
- 19. Равнобедренный треугольник.
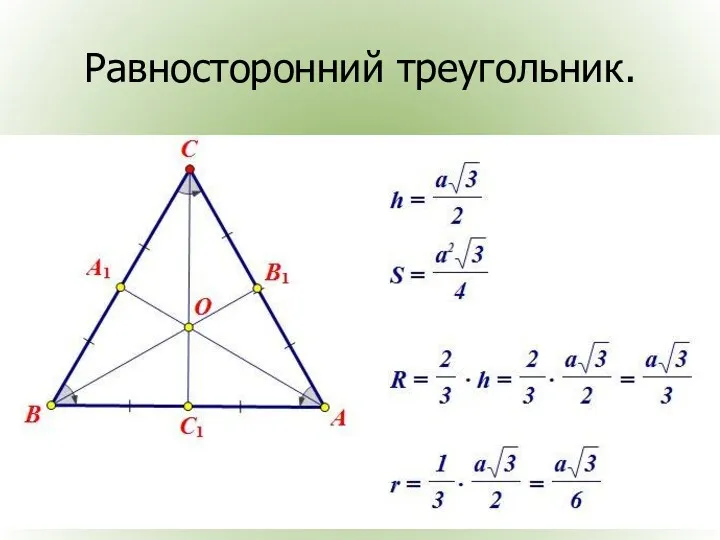
- 20. Равносторонний треугольник.
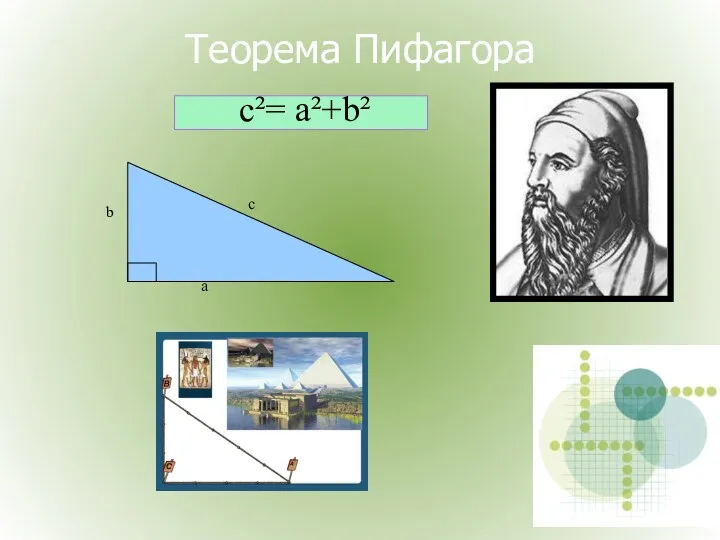
- 21. Теорема Пифагора c²= а²+b²
- 22. Доказательство теоремы Пифагора Дано: а,b- катеты, с-гипотенуза. Доказать: a2+b2=c2. Доказательство: Достроим до квадрата со стороной (a+b).
- 23. Вот задача индийского математика 12в. Бхаскары На берегу реки рос тополь одинокий. Вдруг ветра порыв его
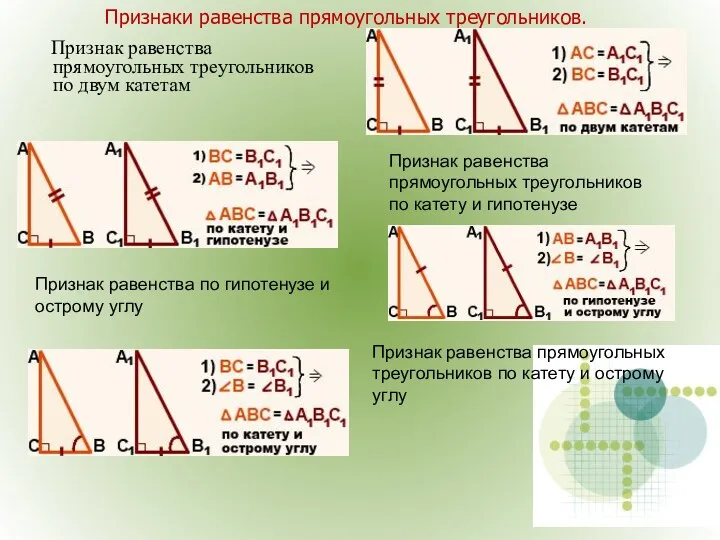
- 24. Признаки равенства прямоугольных треугольников. Признак равенства прямоугольных треугольников по двум катетам Признак равенства прямоугольных треугольников по
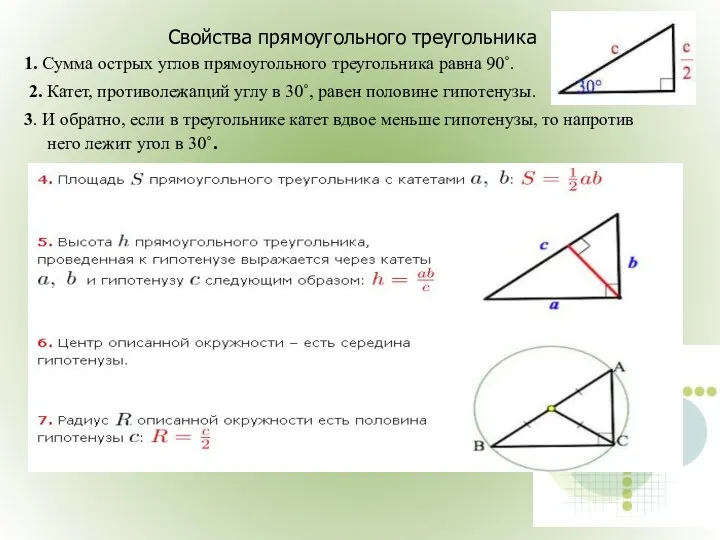
- 25. Свойства прямоугольного треугольника 1. Сумма острых углов прямоугольного треугольника равна 90˚. 2. Катет, противолежащий углу в
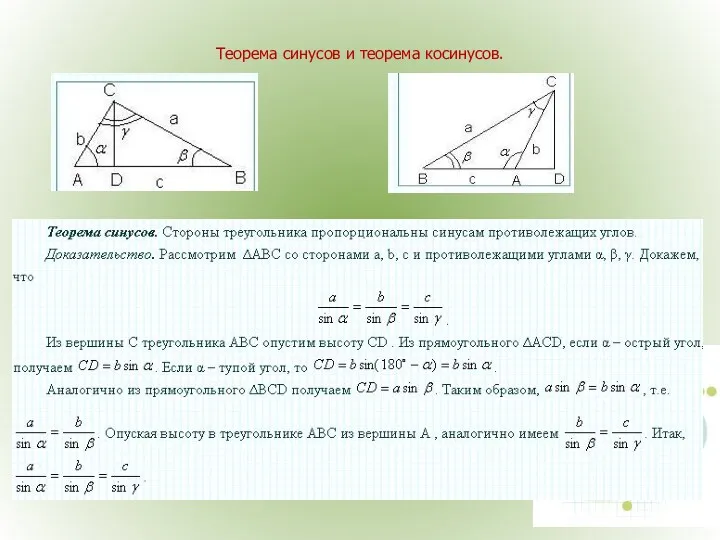
- 26. Теорема синусов и теорема косинусов.
- 27. Теорема косинусов.
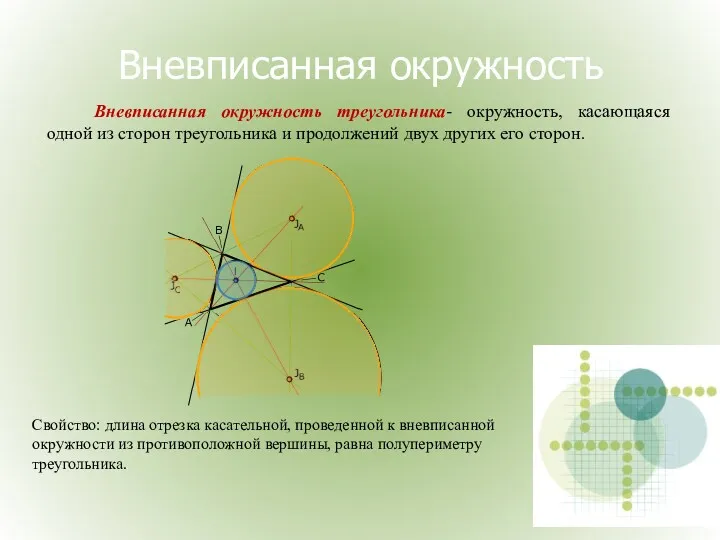
- 28. Вневписанная окружность Вневписанная окружность треугольника- окружность, касающаяся одной из сторон треугольника и продолжений двух других его
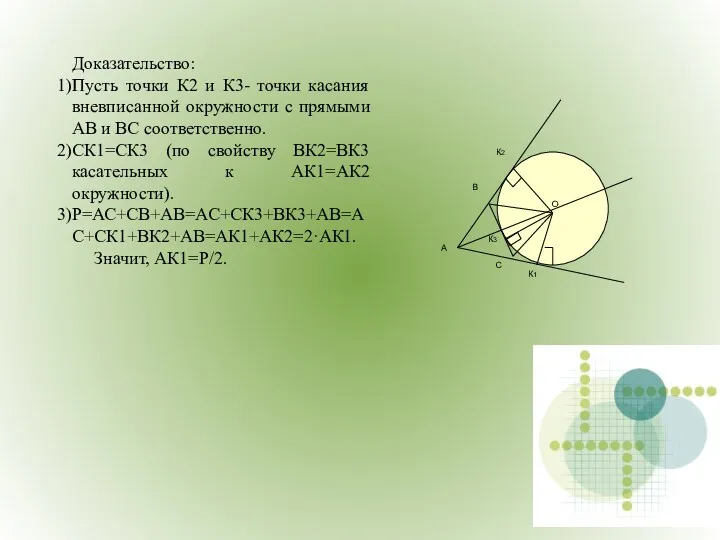
- 29. Доказательство: Пусть точки К2 и К3- точки касания вневписанной окружности с прямыми АВ и ВС соответственно.
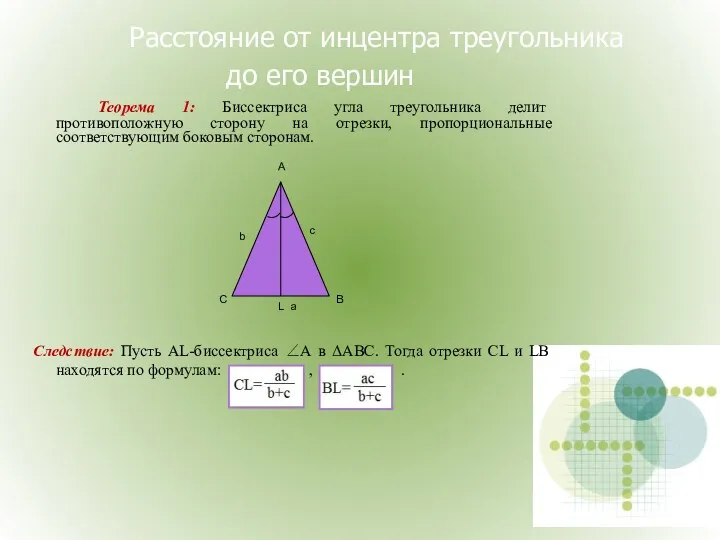
- 30. Расстояние от инцентра треугольника до его вершин Теорема 1: Биссектриса угла треугольника делит противоположную сторону на
- 31. Дано: ВК- биссектриса, СМ||ВК Доказательство: Так как ВК – биссектриса ∠АВС, то ∠АВК=∠КВС. Далее, ∠АВК=∠ВМС, как
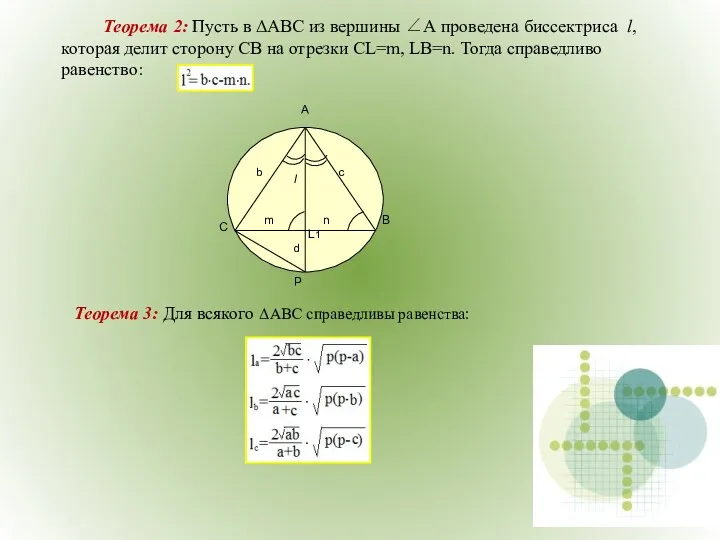
- 32. Теорема 2: Пусть в ΔАВС из вершины ∠А проведена биссектриса l, которая делит сторону СВ на
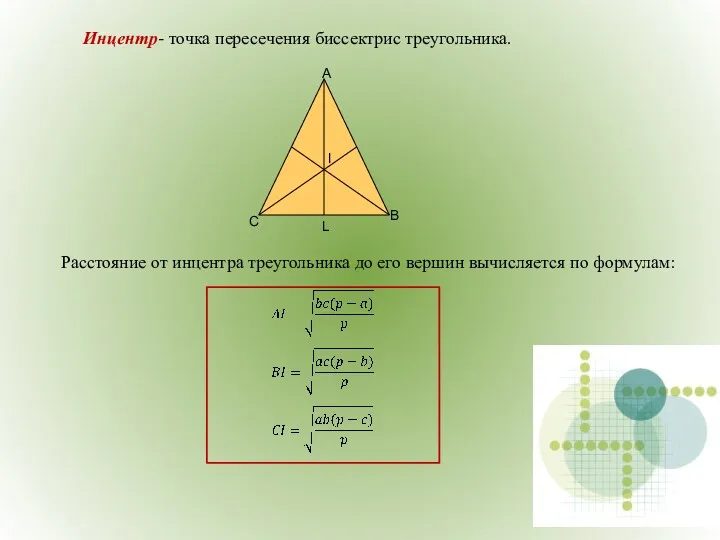
- 33. Инцентр- точка пересечения биссектрис треугольника. Расстояние от инцентра треугольника до его вершин вычисляется по формулам:
- 34. Свойства медиан Теорема: Если a, b, с- стороны ΔАВС (рис.34), ma, mb, mc- его медианы, проведенные
- 37. Задача
- 38. Спасибо за внимание!
- 40. Скачать презентацию











 Построение кусочно-линейной функции
Построение кусочно-линейной функции Порівняння десяткових дробів. Математика. 5 клас
Порівняння десяткових дробів. Математика. 5 клас система координат на плоскости
система координат на плоскости Преобразование Фурье. Лекция 20
Преобразование Фурье. Лекция 20 Презентация к уроку математики по теме Дроби 4 класс
Презентация к уроку математики по теме Дроби 4 класс Математика. 1 класс. Урок 71. Уравнение. Проверка решения уравнения - Презентация
Математика. 1 класс. Урок 71. Уравнение. Проверка решения уравнения - Презентация Введение в метрологию
Введение в метрологию Тренажёр В гости к Матроскину. Математика 1 класс
Тренажёр В гости к Матроскину. Математика 1 класс Первый признак подобия треугольников
Первый признак подобия треугольников Дидактическая игра по ФЭМП для детей во второй младшей группе
Дидактическая игра по ФЭМП для детей во второй младшей группе Числа от 1-8. УМК Школа 2100
Числа от 1-8. УМК Школа 2100 20231203_zadachi_na_rabotu
20231203_zadachi_na_rabotu Случаи сложения и вычитания, основанные на знании нумерации чисел
Случаи сложения и вычитания, основанные на знании нумерации чисел Формирование математических представлений детей дошкольного возраста посредством дидактических игр
Формирование математических представлений детей дошкольного возраста посредством дидактических игр Решение задач. Площади поверхности
Решение задач. Площади поверхности Сложение и вычитание двузначных чисел
Сложение и вычитание двузначных чисел Числа до 10 в порядке возрастания
Числа до 10 в порядке возрастания Теория вероятностей и комбинаторные правила для решения задачи ЕГЭ В6
Теория вероятностей и комбинаторные правила для решения задачи ЕГЭ В6 ПРИЕМ ПИСЬМЕННОГО ВЫЧИТАНИЯ ДЛЯ СЛУЧАЕВ ВИДА 7 000 – 345, 37 007 – 18 032
ПРИЕМ ПИСЬМЕННОГО ВЫЧИТАНИЯ ДЛЯ СЛУЧАЕВ ВИДА 7 000 – 345, 37 007 – 18 032 устный счет, переход через десяток
устный счет, переход через десяток Теория вероятностей. Простейшие правила и формулы вычисления вероятностей
Теория вероятностей. Простейшие правила и формулы вычисления вероятностей Квадратный трехчлен. 8 класс
Квадратный трехчлен. 8 класс Определение конуса
Определение конуса Математическое моделирование
Математическое моделирование Геометрия для малышей
Геометрия для малышей Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Случаи сложения и вычитания, основанные на знаниях нумерации
Случаи сложения и вычитания, основанные на знаниях нумерации Основные моменты тригонометрии
Основные моменты тригонометрии