Содержание
- 2. 1.Уравнение прямой с угловым коэффициентом: y=kx+b k- угловой коэффициент прямой α x y o b α
- 3. Уравнение прямой, проходящей через точку М1(х1;у1) с заданным угловым коэффициентом k, при α x y o
- 4. Уравнение прямой, проходящей через точку М1(х1;у1), но не имеющей углового коэффициента, при Х=Х1 x y o
- 5. Уравнение прямой, проходящей через две заданные точки М1(х1;у1) и М2(х2;у2) x y o y2 М1 x1
- 6. Уравнение прямой, проходящей через две заданные точки М1(х1;у1) и М2(х2;у2) x2 x1 y o М2 М1
- 7. Общее уравнение прямой на плоскости: Ax+By+C=0, где А,В,С – числа Если А=0 В=0 уравнение прямой принимает
- 8. 1. Угловой коэффициент прямой, проходящей через две точки М1(х1;у1) и М2(х2;у2) ПРИЛОЖЕНИЯ
- 9. 2. Острый угол φ между прямыми, заданными уравнениями y=k1x+b1 и y=k2x+b2 вычисляется по формуле: ПРИЛОЖЕНИЯ
- 10. 3. Точка пересечения прямых, заданных общими уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, находится как решение системы: ПРИЛОЖЕНИЯ
- 11. 4. Координаты x0 ,y0 середины отрезка M1 , M2 между точками М1(х1;у1) и М2(х2;у2) ПРИЛОЖЕНИЯ
- 12. 5. Расстояние |M1M2| между точками М1(х1;у1) и М2(х2;у2) ПРИЛОЖЕНИЯ
- 13. 6. Необходимое и достаточное условие параллельности двух прямых Необходимое и достаточное условие параллельности двух прямых, имеющих
- 14. 7. Необходимое и достаточное условие перпендикулярности двух прямых Необходимое и достаточное условие перпендикулярности двух прямых, имеющих
- 15. Примеры: П р и м е р 1. Дано общее уравнение прямой: Найти угловой коэффициент прямой.
- 16. Примеры: П р и м е р 2. Составить уравнение прямой, проходящей через точку А(-1;3) и
- 17. Примеры: П р и м е р 3. Составить уравнение прямой, проходящей через точку пересечения прямых:
- 18. Примеры: Найдем угловой коэффициент k1 прямой: Из условия параллельности двух прямых находим угловой коэффициент искомой прямой:
- 19. Нормальный вектор прямой Если вектор перпендикулярен направляющему вектору прямой , то он называется нормальным вектором прямой
- 20. Нормальный вектор прямой Найти уравнение прямой , которая проходит через точку и имеет нормальный вектор .
- 21. Расстояние от точки до прямой Теорема. Расстояние от точки до прямой, заданной общим уравнением вычисляется формулой
- 22. Расстояние от точки до прямой Найти расстояние от точки до прямой, заданной общим уравнением Решение. Ответ:
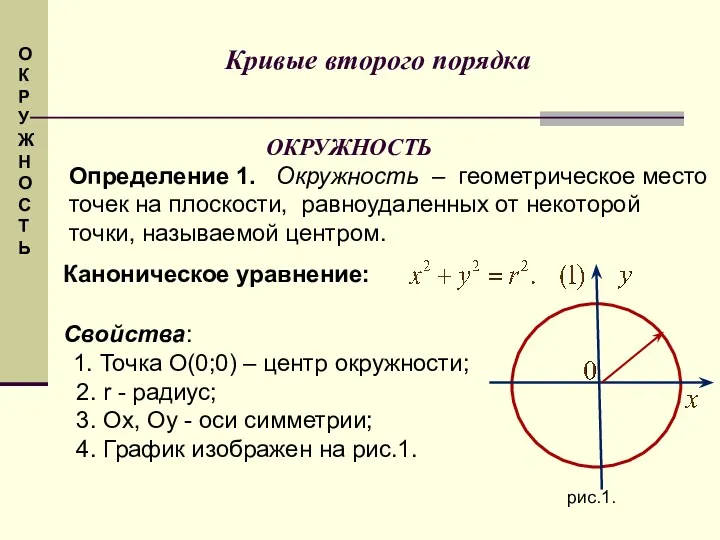
- 23. Кривые второго порядка ОКРУЖНОСТЬ Определение 1. Окружность – геометрическое место точек на плоскости, равноудаленных от некоторой
- 24. Кривые второго порядка О К Р У Ж Н О С Т Ь обладает свойствами: Окружность,
- 25. Определение. Эллипс – геометрическое место точек на плоскости, для каждой из которых сумма расстояний до двух
- 26. Свойства: 1. Центр эллипса − точка О(0;0); 2. Вершины эллипса − точки 3. − оси эллипса;
- 27. Кривые второго порядка Эллипс, задаваемый уравнением обладает свойствами: Э ллипс
- 28. Кривые второго порядка Определение. Гипербола – геометрическое место точек на плоскости, для каждой из которых модуль
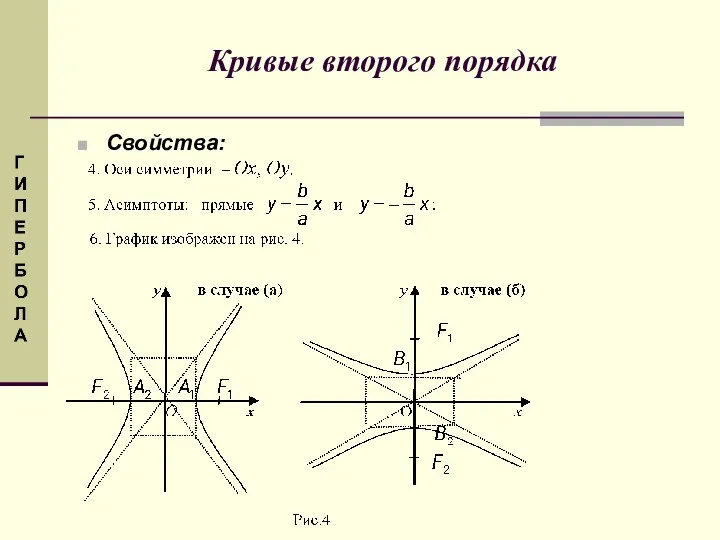
- 29. Свойства: Кривые второго порядка
- 30. Свойства: Кривые второго порядка
- 31. Гиперболы, задаваемые уравнениями: Кривые второго порядка Вершины:
- 32. Кривые второго порядка П А Р А Б О Л А где некоторое число, называемое параметром
- 33. Кривые второго порядка П А Р А Б О Л А Свойства: Вершина: О(0;0); Фокусы параболы:
- 34. Кривые второго порядка П А Р А Б О Л А ; Вершина: точка Фокусы параболы:
- 36. Скачать презентацию































 Теоремы дифференциального исчисления. Тема 10
Теоремы дифференциального исчисления. Тема 10 Задача по математике (4 класс)
Задача по математике (4 класс) Параллельные прямые
Параллельные прямые Алгебра. Лекция 3. Простые и составные числа. Основная теорема арифметики
Алгебра. Лекция 3. Простые и составные числа. Основная теорема арифметики Треугольники
Треугольники Золотое сечение
Золотое сечение Решение дробных рациональных уравнений
Решение дробных рациональных уравнений Элементы комбинаторики
Элементы комбинаторики Правила построения рядов динамики
Правила построения рядов динамики Площадь многоугольника. Единицы измерения площадей. Свойства площадей
Площадь многоугольника. Единицы измерения площадей. Свойства площадей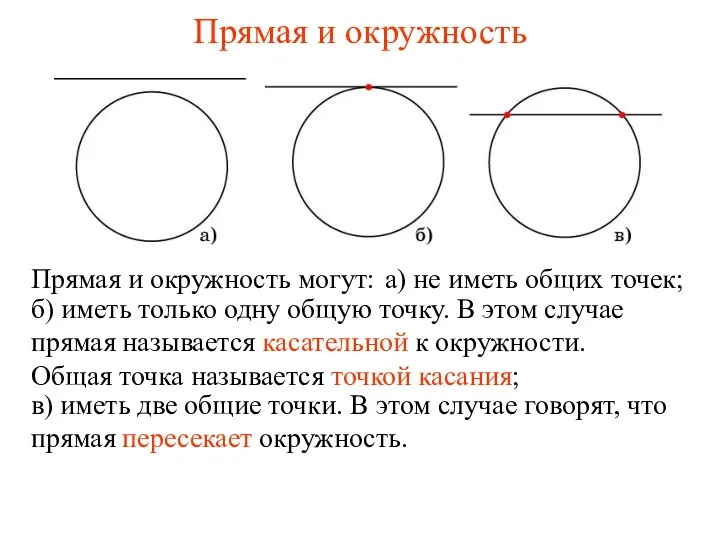 Прямая и окружность
Прямая и окружность Құрама есептер
Құрама есептер Случаи вычитания 11-
Случаи вычитания 11- Задания по математике. Вариант 4
Задания по математике. Вариант 4 Штангенциркуль. Измерение штангенциркулем
Штангенциркуль. Измерение штангенциркулем Математический кружок. Занятие 3. Инварианты
Математический кружок. Занятие 3. Инварианты Виды треугольников
Виды треугольников Математика 4 класс. Проектная работа Старинные меры длины
Математика 4 класс. Проектная работа Старинные меры длины Электронная презентация к уроку математики на тему: Треугольники.
Электронная презентация к уроку математики на тему: Треугольники. Учимся писать цифру 3
Учимся писать цифру 3 Преобразование графиков функции
Преобразование графиков функции Урок математики Распределительное свойство умножения относительно сложения 4 класс
Урок математики Распределительное свойство умножения относительно сложения 4 класс Многогранники и круглые тела
Многогранники и круглые тела Неопределенный интеграл. §1. Неопределенный интеграл и его свойства
Неопределенный интеграл. §1. Неопределенный интеграл и его свойства Вычисление площадей плоских фигур с помощью определенного интеграла
Вычисление площадей плоских фигур с помощью определенного интеграла Презентация по математике Произведение и множетели
Презентация по математике Произведение и множетели Поняття десяткового дробу
Поняття десяткового дробу Отчёт по проекту Учебный комплекс по математике для учащихся начальной школы.
Отчёт по проекту Учебный комплекс по математике для учащихся начальной школы.