Содержание
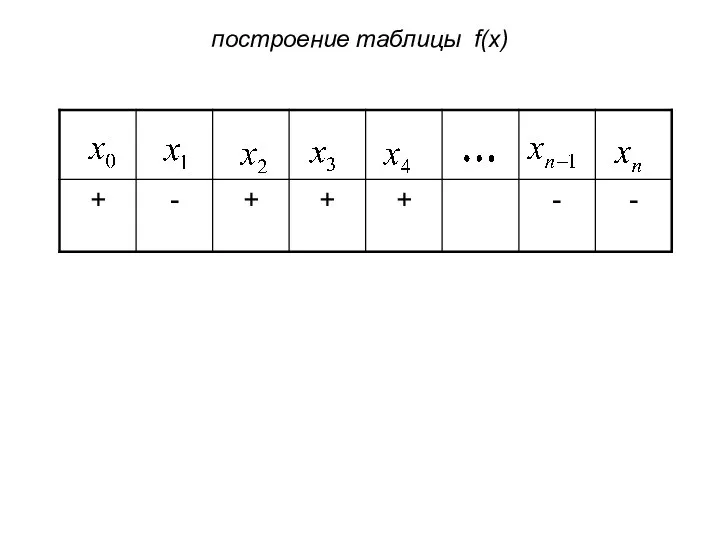
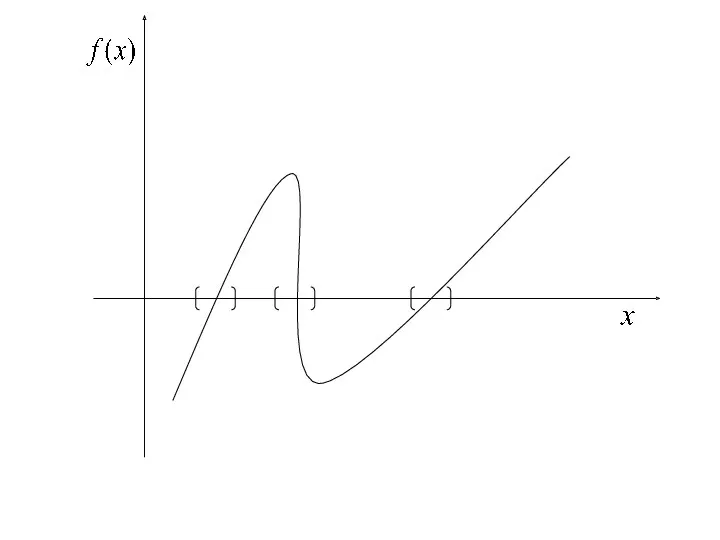
- 2. построение таблицы f(x)
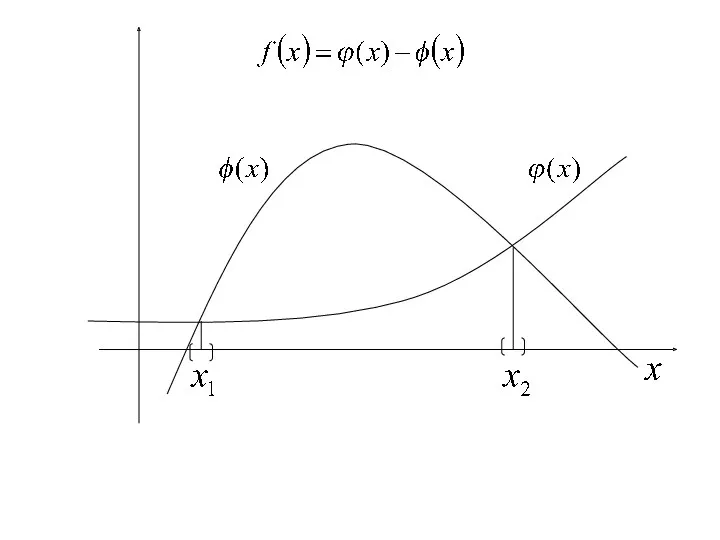
- 3. для многочлена если выполнены неравенства то положительные корни не превосходят действительно:
- 6. 1. Дихотомия Метод деления пополам Метод бисекции
- 7. 2. Метод простой итерации Исследуем условия сходимости:
- 8. метод не сходится вообще метод сходится при любом начальном приближении Пример
- 9. Условие окончания итерационного цикла если приближения то слева, то справа от корня тогда если приближения с
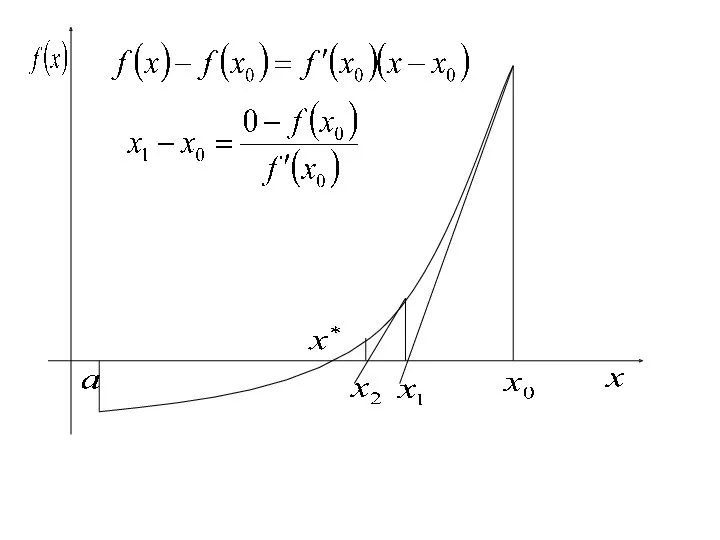
- 10. 3. Метод Ньютона Метод касательных Метод линеаризации
- 12. сходимость метода Ньютона скорость сходимости метода Ньютона
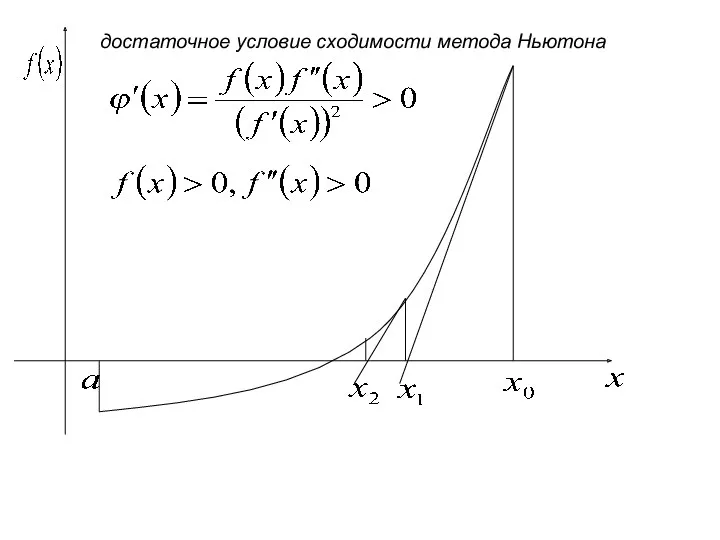
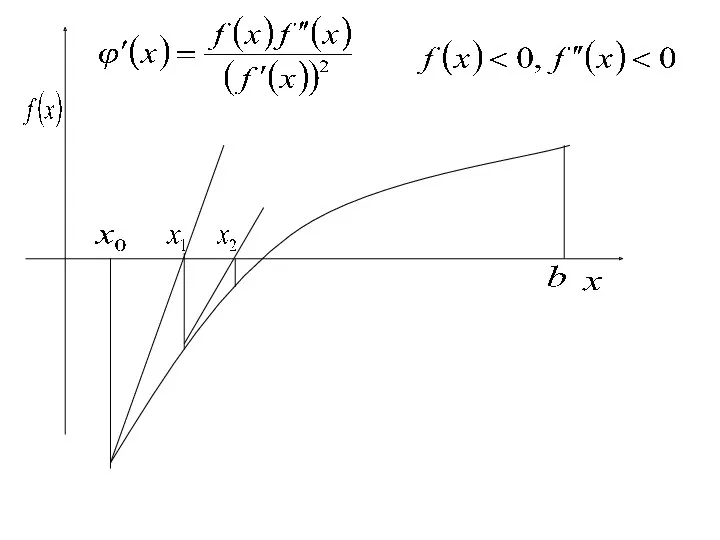
- 13. достаточное условие сходимости метода Ньютона
- 16. 4. Модифицированный метод Ньютона Если тогда для уменьшения количества арифметических операций на одном шаге итерации используется
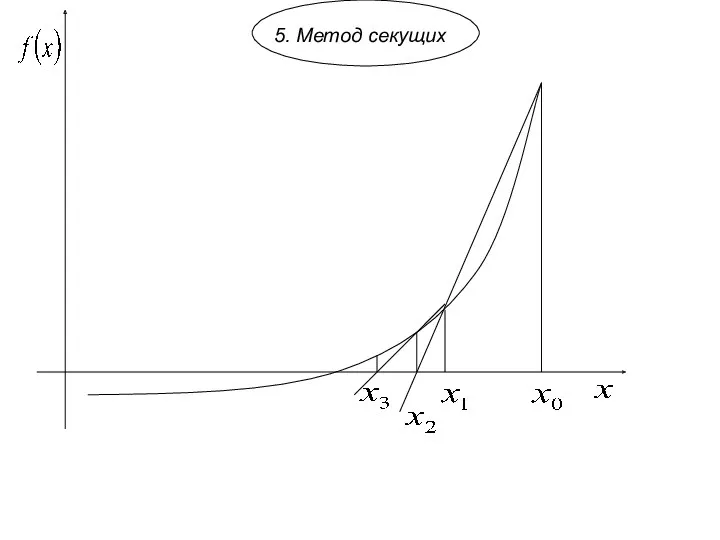
- 17. 5. Метод секущих
- 18. Уравнение прямой преимущества метода секущих: простота реализации нет производных недостатки метода секущих: неизбежные погрешности, возникающие при
- 20. но с другой стороны, по формуле Тейлора числитель равен следовательно
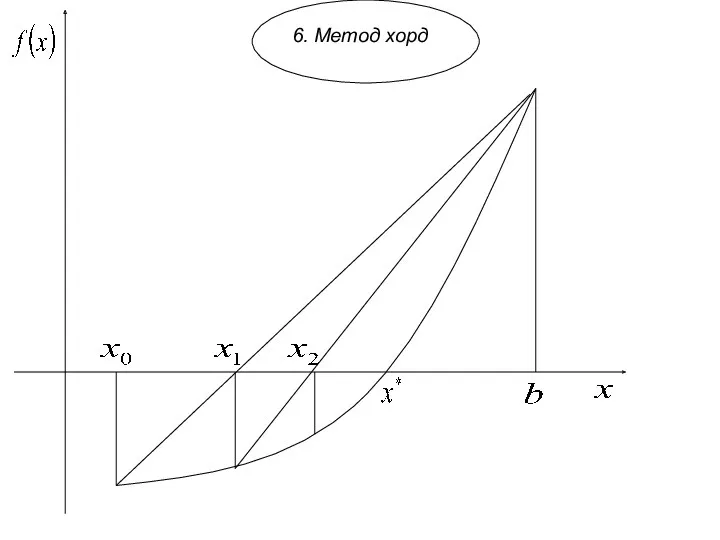
- 21. 6. Метод хорд
- 22. Уравнение хорды если неподвижный правый конец отрезка: в получаем ограниченную сверху монотонно возрастающую последовательность приближений
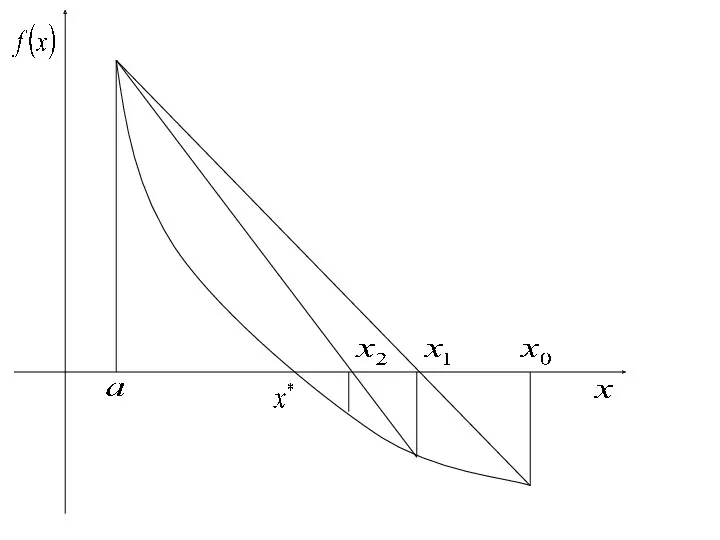
- 24. если неподвижный левый конец отрезка: а получаем ограниченную снизу монотонно убывающую последовательность приближений возможны варианты: 1.
- 25. Другие методы решения нелинейного уравнения Метод Шредера: Классификация методов решения Метод простой итерации, послед. приближений Метод
- 26. Метод Чебышёва построения итерационных процессов высшего порядка Предположим, что существует функция g(u), обратная к f(u). При
- 27. метод секущих – установление факта о сверхлинейной сходимости метода Вержбицкий В.М. Численные методы (линейная алгебра и
- 28. Продолжение рассмотрения метода Ньютона ≈ 300 лет назад Токакадзу ║ с Ньютоном открыл метод если х
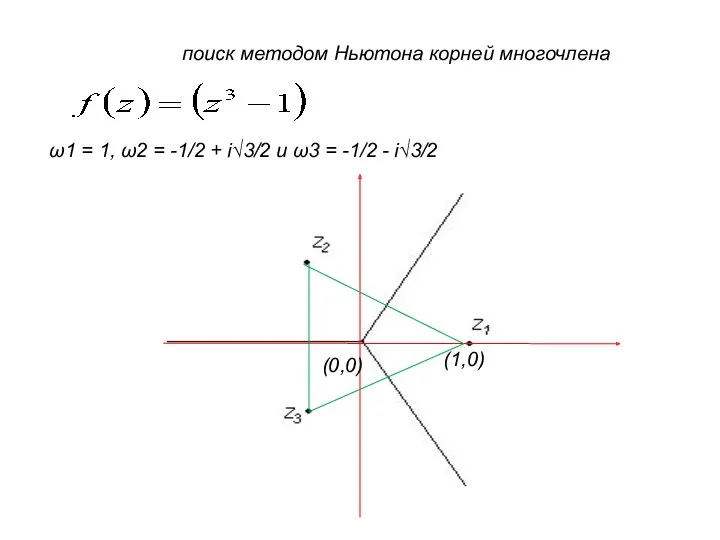
- 29. поиск методом Ньютона корней многочлена ω1 = 1, ω2 = -1/2 + i√3/2 и ω3 =
- 30. фрактал - бассейн Ньютона
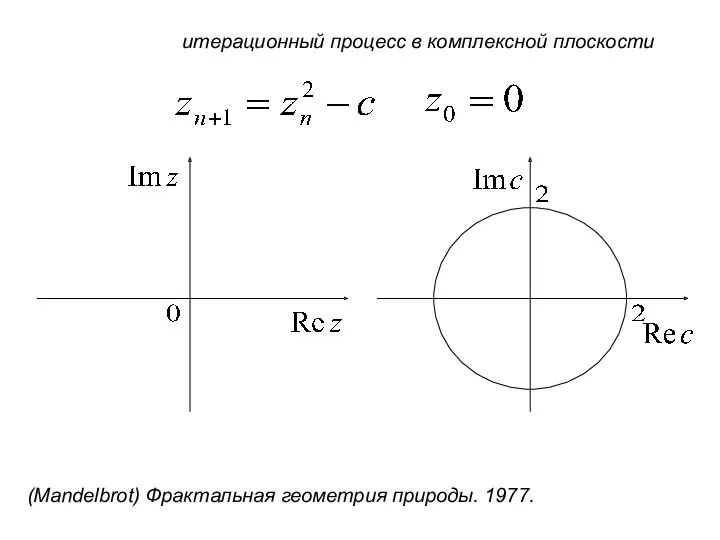
- 33. (Mandelbrot) Фрактальная геометрия природы. 1977. итерационный процесс в комплексной плоскости
- 35. Скачать презентацию







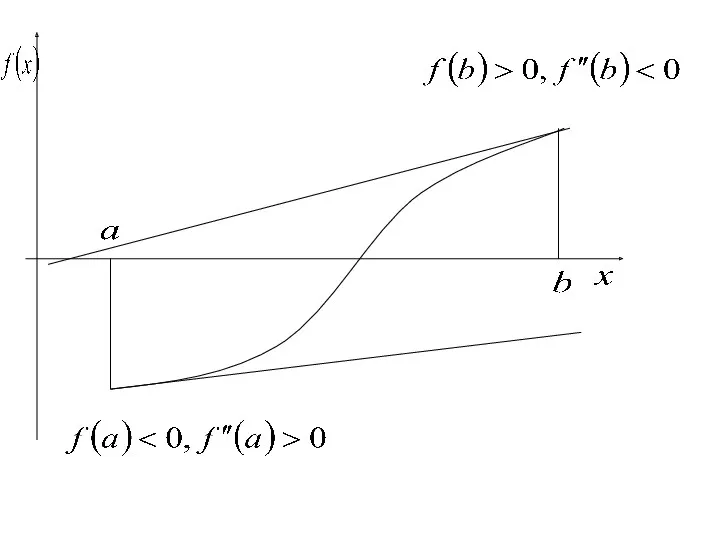


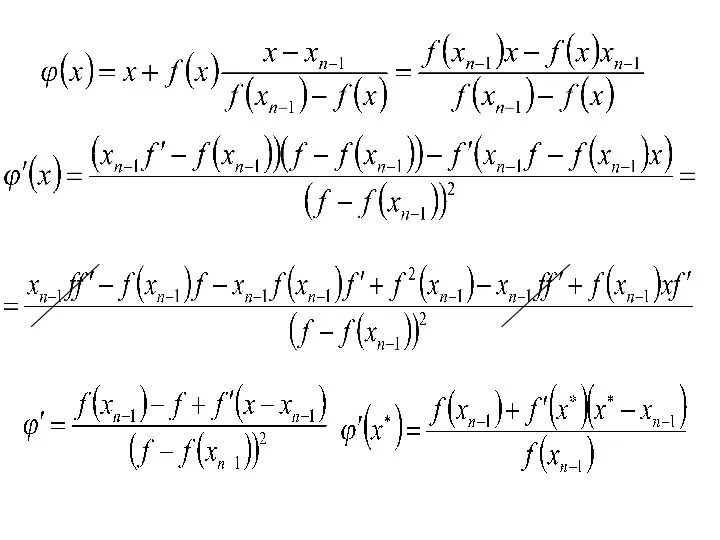










 Единицы площади (математика, 3 класс, УМК Гармония)
Единицы площади (математика, 3 класс, УМК Гармония) Ортогональная проекция многоугольника и ее площадь
Ортогональная проекция многоугольника и ее площадь Математика 2 класс Для устного счета
Математика 2 класс Для устного счета Понятие вектора в пространстве
Понятие вектора в пространстве Математика М.И.Моро. УМК Школа России 1 класс. Устный счёт.
Математика М.И.Моро. УМК Школа России 1 класс. Устный счёт. Понятие предела числовой последовательности. Предел функции в точке и на бесконечности. Теоремы о пределах функции
Понятие предела числовой последовательности. Предел функции в точке и на бесконечности. Теоремы о пределах функции Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов Вписанный в окружность треугольник
Вписанный в окружность треугольник Применение дифференциала в приближенных вычислениях
Применение дифференциала в приближенных вычислениях Памятка по оформлению краткой записи к задачам. 1-2 класс
Памятка по оформлению краткой записи к задачам. 1-2 класс Квадратные неравенства (8 класс)
Квадратные неравенства (8 класс) Развёрнутый конспект урока математики в 1 классе по программе Л.Г. Петерсон Равные фигуры
Развёрнутый конспект урока математики в 1 классе по программе Л.Г. Петерсон Равные фигуры Интегрированное занятие по ФЭМП в средней группе
Интегрированное занятие по ФЭМП в средней группе Треугольники. Классификация треугольников. 7 класс
Треугольники. Классификация треугольников. 7 класс Дискретные случайные величины
Дискретные случайные величины КВМ. Задачи. 6 класс
КВМ. Задачи. 6 класс Recall the definitions of position, distance, displacement, velocity and acceleration
Recall the definitions of position, distance, displacement, velocity and acceleration Объёмы геометрических тел
Объёмы геометрических тел Сокращение дробей. Задание для устного счета. Упражнение 6. 6 класс
Сокращение дробей. Задание для устного счета. Упражнение 6. 6 класс Метод математической индукции
Метод математической индукции урок по математике Письменное сложение трехзначных чисел
урок по математике Письменное сложение трехзначных чисел Функции, их свойства и графики. Урок – повторение в 9 классе
Функции, их свойства и графики. Урок – повторение в 9 классе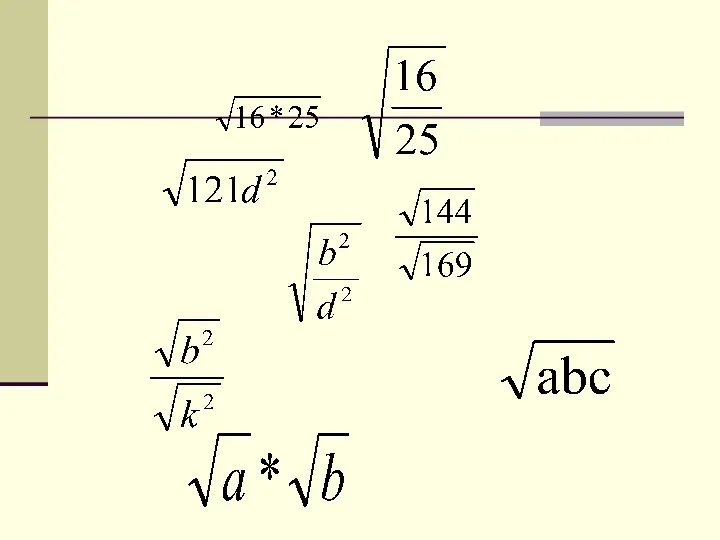 Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Быстрее, сильнее и правильнее. Пусть ум победит силу
Быстрее, сильнее и правильнее. Пусть ум победит силу Шар, конус, цилиндр
Шар, конус, цилиндр Сумма углов треугольника. Внешний угол треугольника (7 класс)
Сумма углов треугольника. Внешний угол треугольника (7 класс) Вторая производная и ее физический смысл
Вторая производная и ее физический смысл