Слайд 2

Вписанный шар в пирамиду.
1. В треугольную пирамиду можно вписать шар.
2. В пирамиду, у которой в основание можно вписать окружность, центр которой служит основанием высоты пирамиды, можно вписать шар.
Следствие. В любую правильную пирамиду можно вписать шар.
3. Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.
Слайд 3
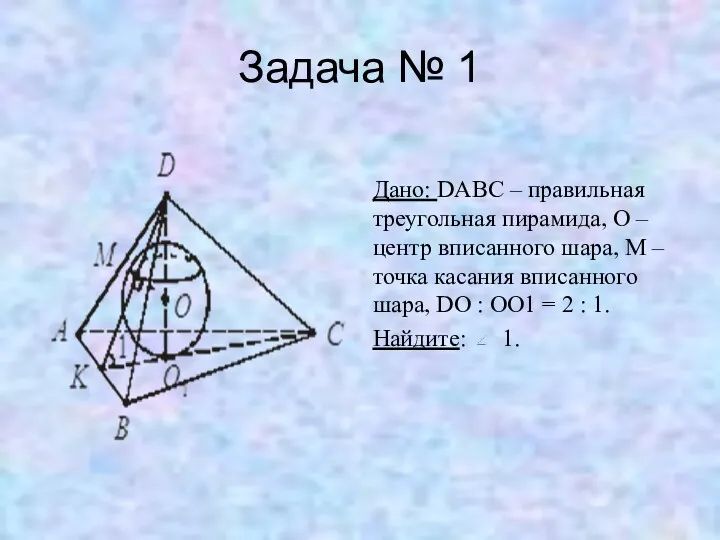
Задача № 1
Дано: DABC – правильная треугольная пирамида, O – центр
вписанного шара, M – точка касания вписанного шара, DO : OO1 = 2 : 1.
Найдите: 1.
Слайд 4
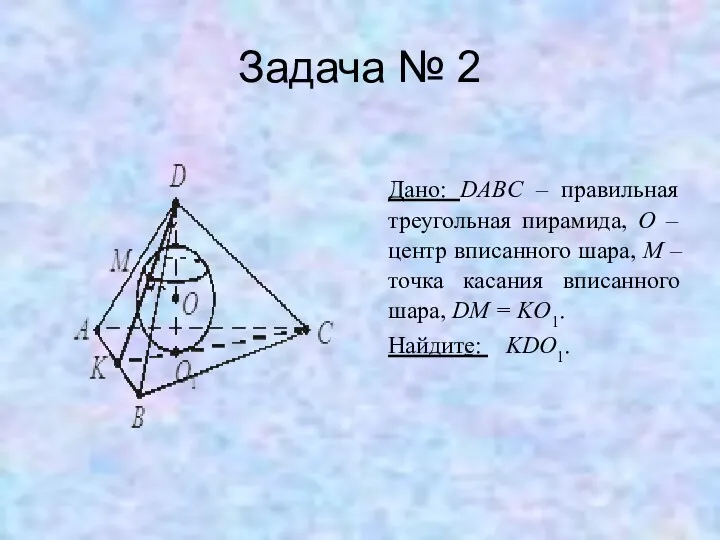
Задача № 2
Дано: DABC – правильная треугольная пирамида, O – центр
вписанного шара, M – точка касания вписанного шара, DM = KO1.
Найдите: KDO1.
Слайд 5
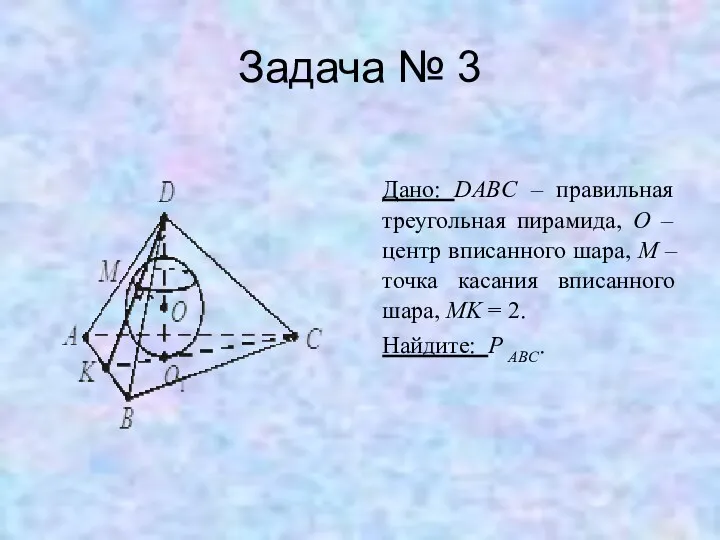
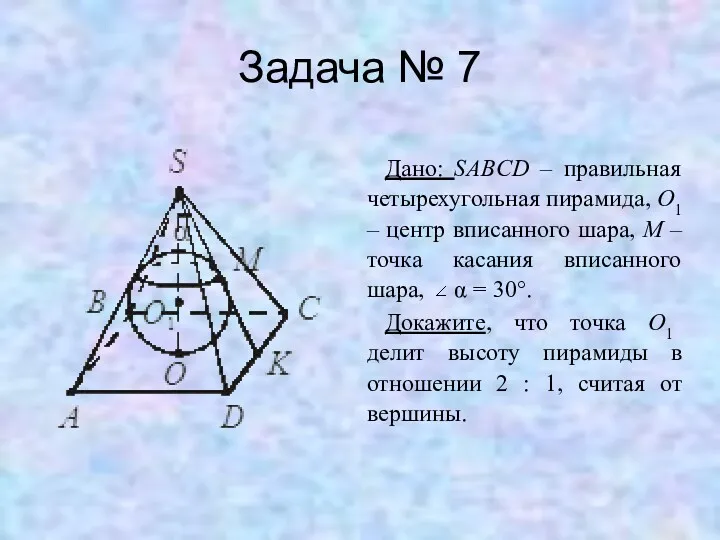
Задача № 3
Дано: DABC – правильная треугольная пирамида, O – центр
вписанного шара, M – точка касания вписанного шара, MK = 2.
Найдите: P ABC.
Слайд 6
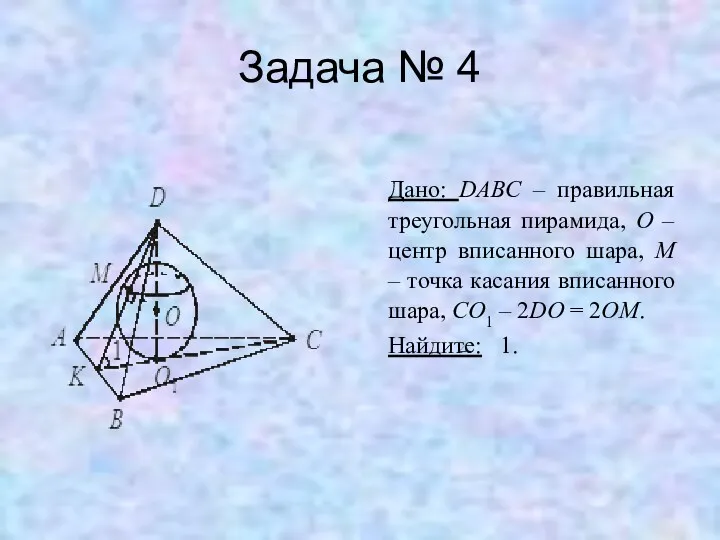
Задача № 4
Дано: DABC – правильная треугольная пирамида, O – центр
вписанного шара, M – точка касания вписанного шара, CO1 – 2DO = 2OM.
Найдите: 1.
Слайд 7
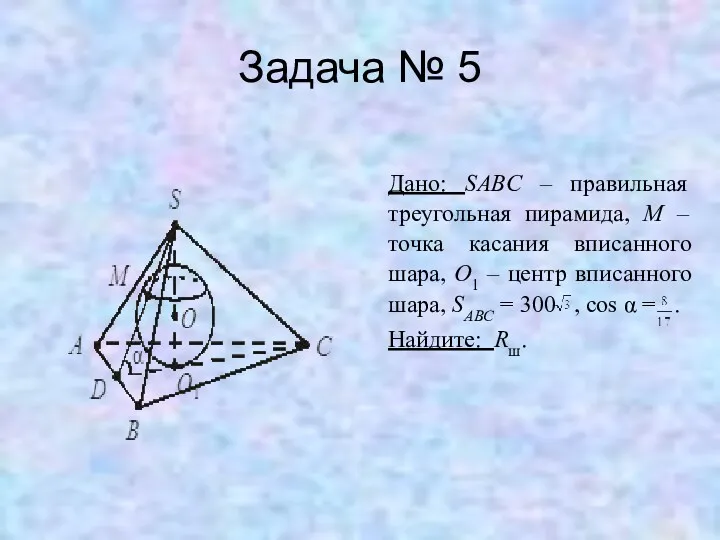
Задача № 5
Дано: SABC – правильная треугольная пирамида, M – точка
касания вписанного шара, O1 – центр вписанного шара, SABC = 300 , cos α = .
Найдите: Rш.
Слайд 8
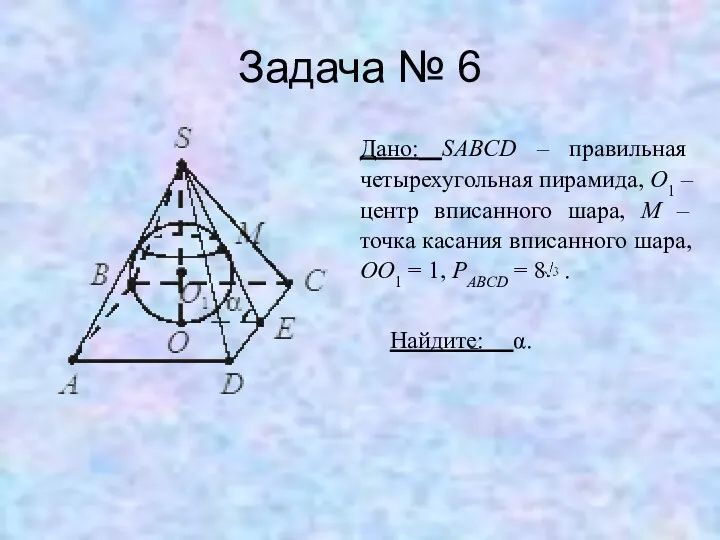
Задача № 6
Дано: SABCD – правильная четырехугольная пирамида, O1 – центр
вписанного шара, M – точка касания вписанного шара, OO1 = 1, PABCD = 8 .
Найдите: α.
Слайд 9
Слайд 10

Описанный около пирамиды шар.
1. Около треугольной пирамиды можно описать шар.
2. Если около основания пирамиды можно описать окружность, то около пирамиды можно описать шар.
Следствие. Около любой правильной пирамиды можно описать шар.
3. Центр шара, описанного около пирамиды, лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности, и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
Следствие. Центр описанной около правильной пирамиды сферы лежит на высоте этой пирамиды.
Слайд 11
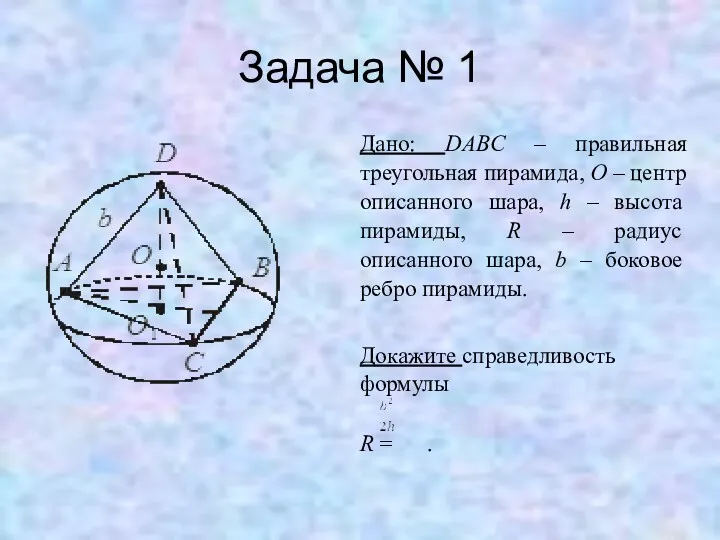
Задача № 1
Дано: DABC – правильная треугольная пирамида, O – центр
описанного шара, h – высота пирамиды, R – радиус описанного шара, b – боковое ребро пирамиды.
Докажите справедливость формулы
R = .
Слайд 12

Задача № 2.
Дано: DABC – правильная треугольная пирамида, O – центр
описанного шара,
DO1 : O1O = 2 : 1.
Найдите: DAO.
Слайд 13
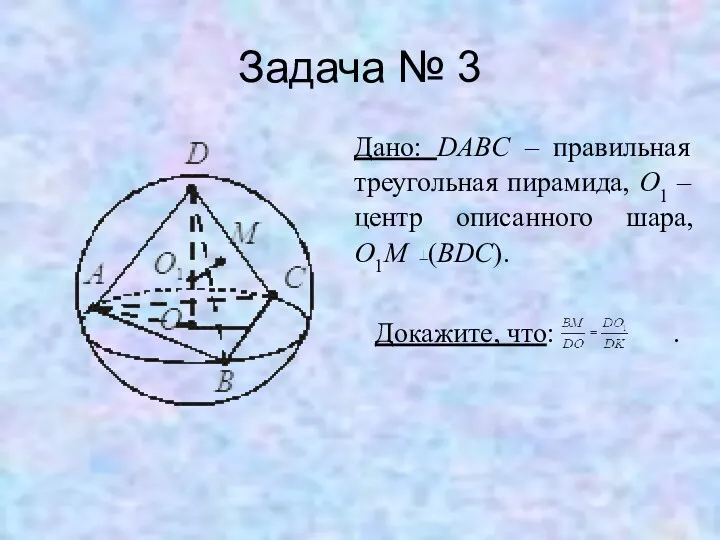
Задача № 3
Дано: DABC – правильная треугольная пирамида, O1 – центр
описанного шара,
O1M (BDC).
Докажите, что: .
Слайд 14

Задача № 4
Дано: DABC – правильная треугольная пирамида, O – центр
описанного шара,
DO1 = 4, DC = 5.
Найдите: Rш.
Слайд 15

Задача № 5.
Дано: SABCD – правильная треугольная пирамида, O1 – центр
описанного шара,
DS = DB.
Докажите, что α = 120°.














 Статистикалық жорамалдарды тексеру теориясының негіздері. Параметрлік критерийлер
Статистикалық жорамалдарды тексеру теориясының негіздері. Параметрлік критерийлер Подготовка к ЕГЭ, ГИА. Задачи на часы
Подготовка к ЕГЭ, ГИА. Задачи на часы Программа внеурочной деятельности учащихся начальной школы Загадочная геометрия
Программа внеурочной деятельности учащихся начальной школы Загадочная геометрия Алгоритм деления многозначного числа на однозначное
Алгоритм деления многозначного числа на однозначное Теорема о вероятности суммы событий
Теорема о вероятности суммы событий Golden Ratio
Golden Ratio Кітап беттері
Кітап беттері Состав числа
Состав числа презентация к уроку математики по теме Периметр 2 класс по программе Школа 2100
презентация к уроку математики по теме Периметр 2 класс по программе Школа 2100 Математический брейн-ринг 2 класс.
Математический брейн-ринг 2 класс. Производная. Понятие производной. Производная частных функций
Производная. Понятие производной. Производная частных функций Упрощение выражений
Упрощение выражений Измерение высоты дерева способом двух товарищей
Измерение высоты дерева способом двух товарищей Презентации к урокам Диск
Презентации к урокам Диск Презентация к уроку математики по теме Вместимость, 2 класс.
Презентация к уроку математики по теме Вместимость, 2 класс. Метрологические службы федеральных органов управления юридических лиц. (Лекция 3)
Метрологические службы федеральных органов управления юридических лиц. (Лекция 3) Вычисление производных
Вычисление производных Объём фигуры. Единицы объёма
Объём фигуры. Единицы объёма Моделирование систем защиты информации. (Лекция 1)
Моделирование систем защиты информации. (Лекция 1) Why did or didn’t you like Math at school?
Why did or didn’t you like Math at school? Прямоугольный параллелепипед
Прямоугольный параллелепипед Урок математики в 8 классе по теме Многоугольники
Урок математики в 8 классе по теме Многоугольники Проверка значимости в парной линейной регрессии
Проверка значимости в парной линейной регрессии Столбчатые диаграммы
Столбчатые диаграммы тест по математике для 2 класса, конец года
тест по математике для 2 класса, конец года Chapter 3. Polynomial and Rational Functions. 3.4 Zeros of Polynomial Functions
Chapter 3. Polynomial and Rational Functions. 3.4 Zeros of Polynomial Functions Виды параллелограммов. Ромб. Квадрат
Виды параллелограммов. Ромб. Квадрат Прикладная математика. Угол
Прикладная математика. Угол