Слайд 2

Long. And trans. Resonance frequencies
Resonance frequency of the system:
Beam full round-trip
↔ phase 2πq (where q is an integer)
In the FP case this leads to:
Слайд 3

Long. And trans. Resonance frequencies
In FP the mirrors are flat ?
plane waves
For curved mirrors the beams have transversal profile
How does it change the solutions?
Слайд 4

Long. And trans. Resonance frequencies
Reminder: beams and mirrors curvatures are matched
This
means that solving for r=0 is enough
Слайд 5

Long. And trans. Resonance frequencies
The phase condition for half cycle is
thus:
The z-dependent phase of the beam is:
Слайд 6

Long. And trans. Resonance frequencies
Thus we get:
Слайд 7

Long. And trans. Resonance frequencies
From this equation we learn:
The phase depends
on q
The phase depends on transverse characteristics (l,m)
Слайд 8

Long. And trans. Resonance frequencies
We divide the solution into 2 cases:
Constant
l,m
Constant q
Слайд 9

Constant l,m – Longitudinal modes
We write the equation for q and
q+1:
Слайд 10

Constant l,m – Longitudinal modes
We got:
Which is exactly the FSR of
a FP resonator
These modes depend only on the length of the resonator
?they are called, thus, Longitudinal modes
Слайд 11

Constant q – Transverse modes
We write the equation for 2 gaussian
modes:
Слайд 12

Constant q – Transverse modes
We got:
The result is invariant to switching
l and m
Depends on difference in transverse profile (subtraction of l+m)
?they are called, thus, Transverse modes
Слайд 13

Examples – symmetric resonator
Symmetric resonator:
Thus we have:
Слайд 14

Examples – confocal symmetric resonator
Confocal symmetric resonator:
If the resonator is also
confocal:
Слайд 15

Examples – confocal symmetric resonator
Solving L as a function of z0:
Слайд 16

Examples – confocal symmetric resonator
Since the resonator is symmetric:
Слайд 17

Examples – confocal symmetric resonator
Resonance frequencies can:
Coincide with original modes
Be between
two modes
The number of modes in a section is doubled
Слайд 18

Examples – nearly planar resonator
We assume:
Thus we have:
This leads to either:
Слайд 19

Examples – nearly planar resonator
The first option is impossible since by
definition
Thus given we have:
Слайд 20

Examples – nearly planar resonator
So the resonance frequencies are:
Since z0>>L we
have many frequencies between long. freqs.
This is undesirable since quality and coherence are determined by the number of operating modes
Слайд 21

A circular resonator
Given by 3 mirrors on the vertices of an
equilateral triangle
Слайд 22

A circular resonator
The upper (entrance) and left (exit) mirrors are dielectric
mirrors with: r=-r’
The right mirror is fully reflective with R=1
Notice that reflections add π phase and the perimeter of the triangle is L
Слайд 23

A circular resonator
What are the transmission intensity and the resonance frequencies?
Слайд 24

A circular resonator
We calculate the transmission by adding transmitted waves as
we did for FP:
And so on
Слайд 25

A circular resonator
Summing over all the partial waves:
Слайд 26

A circular resonator
The resonance frequencies depend on the cosine of the
phase, not on the sine as in FP
Слайд 27

A circular resonator
Thus the resonance frequencies are shifted, but the FSR
is not changed:
Слайд 28

A circular resonator
We add a mirror between the lower mirrors. Find
the waist of the beam in the resonator
Слайд 29

A circular resonator
We use the analogy to curved mirrors resonators:
L
L/3
Слайд 30

A circular resonator
We can calculate the size as in the curved
mirrors resonator with R=2f:
Слайд 31

A circular resonator
Find νqlm for the first 6 modes for f=L
We
begin with finding the nonlinear phase from the relation of L and z0
Слайд 32

A circular resonator
We notice that the output should gain a phase
of some multiple of 2π over a distance L (not 2L!)
We should also add a π phase on each round due to reflection
Слайд 33

Слайд 34

A circular resonator
The first 6 modes:

































 Решение нестандартных уравнений
Решение нестандартных уравнений Угол между векторами. Скалярное произведение
Угол между векторами. Скалярное произведение Сложение и вычитание смешанных дробей
Сложение и вычитание смешанных дробей Путешествие с цифрами. Тренажёр по математике для 1 класса
Путешествие с цифрами. Тренажёр по математике для 1 класса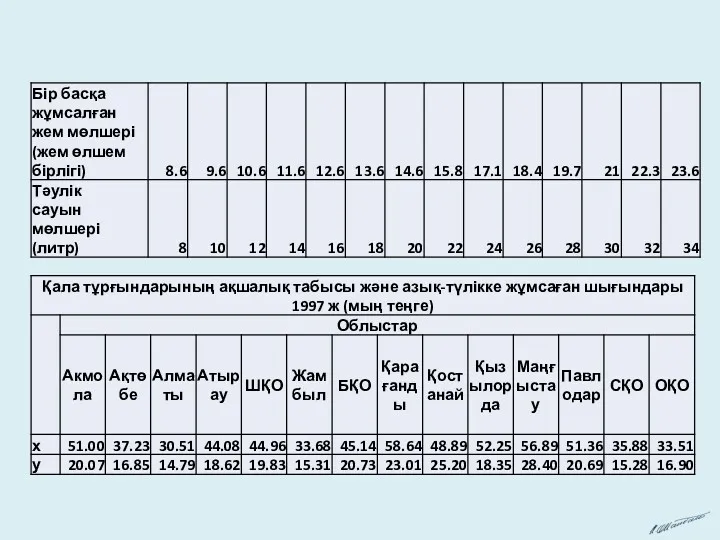 Примеры
Примеры Стереометрические задачи
Стереометрические задачи Положительные и отрицательные числа. Координатная прямая
Положительные и отрицательные числа. Координатная прямая Теорема синусов и косинусов
Теорема синусов и косинусов НОД
НОД Solution methods for bilevel optimization
Solution methods for bilevel optimization Формирование элементарных математических представлений у старших дошкольников с ЗПР.
Формирование элементарных математических представлений у старших дошкольников с ЗПР. Геометрическая алгебра Древней Греции
Геометрическая алгебра Древней Греции Алгебраические и геометрические прогрессии на примере решения практических задач
Алгебраические и геометрические прогрессии на примере решения практических задач Письменное умножение
Письменное умножение Геометрия архитектурной гармонии
Геометрия архитектурной гармонии Подготовка к ЕГЭ по математике. Задание В6 – базовые задачи
Подготовка к ЕГЭ по математике. Задание В6 – базовые задачи Применение производной к исследованию функции
Применение производной к исследованию функции Сумма углов треугольника
Сумма углов треугольника Многогранники. Види многогранників
Многогранники. Види многогранників Урок по математике для 1 класса. Программа Школа России
Урок по математике для 1 класса. Программа Школа России Конкурс красоты, ума и таланта. Мисс Математика
Конкурс красоты, ума и таланта. Мисс Математика Эрудит-марафон
Эрудит-марафон Одночлены. Арифметические операции над одночленами
Одночлены. Арифметические операции над одночленами Деление с остатком. 5 класс
Деление с остатком. 5 класс Қысқаша көбейту формулалары
Қысқаша көбейту формулалары Натуральные числа
Натуральные числа Дискретная математика
Дискретная математика Задачи на движение в разных направлениях (схемы)
Задачи на движение в разных направлениях (схемы)