Содержание
- 2. Bounded Model Checking (BMC) A.I. Planning problems: can we reach a desired state in k steps?
- 3. What is SAT? SATisfying assignment! Given a propositional formula in CNF, find if there exists an
- 4. BMC idea Given: transition system M, temporal logic formula f, and user-supplied time bound k Construct
- 5. BMC idea (cont’d) AG p means p must hold in every state along any path of
- 6. Safety-checking as BMC p is preserved up to k-th transition iff Ω(k) is unsatisfiable: If satisfiable,
- 7. Example: a two bit counter Safety property: AG Ω(2) is unsatisfiable. Ω(3) is satisfiable. Initial state:
- 8. Example: another counter Liveness property: AF Ω(2) is satisfiable Check: EG where Satisfying assignment gives counterexample
- 9. What BMC with SAT Can Do All LTL ACTL and ECTL In principle, all CTL and
- 10. How big should k be? For every model M and LTL property ϕ there exists k
- 11. How big should k be? Diameter d = longest shortest path from an initial state to
- 12. How big should k be? Theorem: for Gp properties CT = d
- 13. How big should k be? Theorem: for Fp properties CT= rd Open Problem: The value of
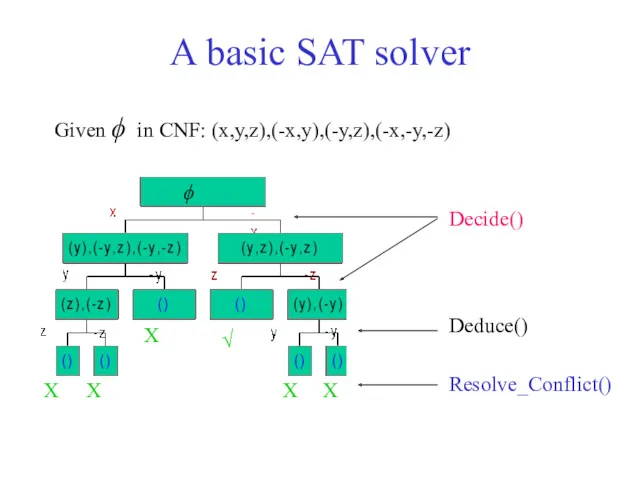
- 14. Given ϕ in CNF: (x,y,z),(-x,y),(-y,z),(-x,-y,-z) Decide() Deduce() Resolve_Conflict() √ X X X X X ϕ A
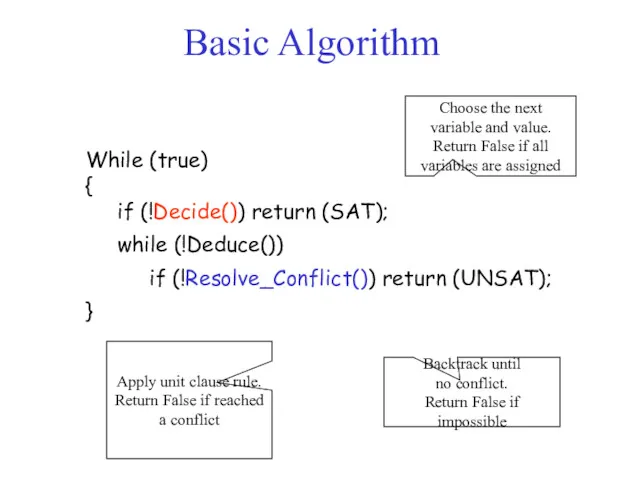
- 15. While (true) { if (!Decide()) return (SAT); while (!Deduce()) if (!Resolve_Conflict()) return (UNSAT); } Choose the
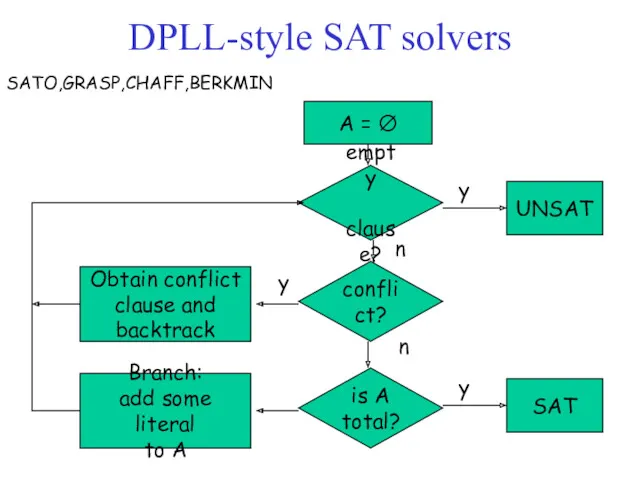
- 16. A = ∅ empty clause? y UNSAT conflict? Obtain conflict clause and backtrack y n is
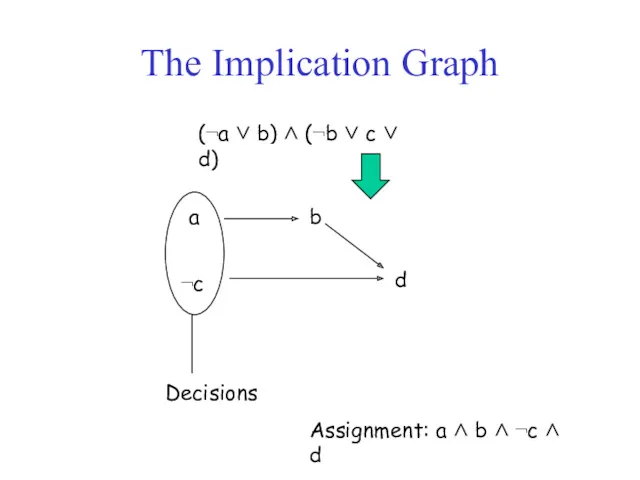
- 17. The Implication Graph (¬a ∨ b) ∧ (¬b ∨ c ∨ d) Assignment: a ∧ b
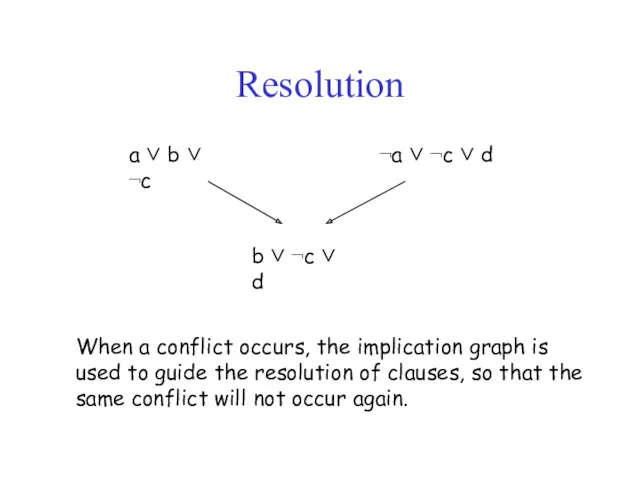
- 18. Resolution a ∨ b ∨ ¬c ¬a ∨ ¬c ∨ d b ∨ ¬c ∨ d
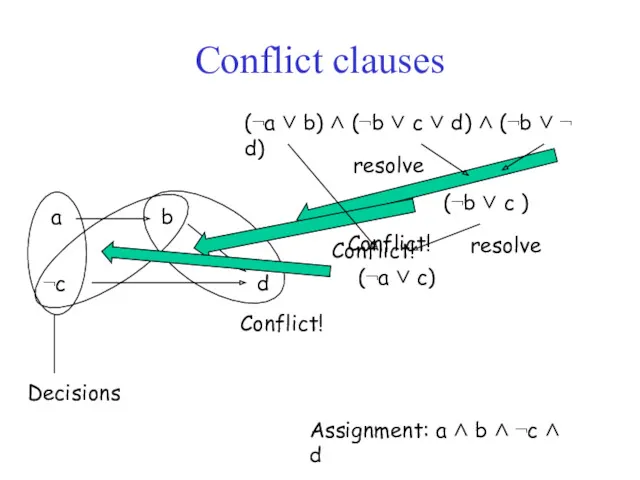
- 19. Conflict clauses (¬a ∨ b) ∧ (¬b ∨ c ∨ d) ∧ (¬b ∨ ¬ d)
- 20. Conflict Clauses (cont.) Conflict clauses: Are generated by resolution Are implied by existing clauses Are in
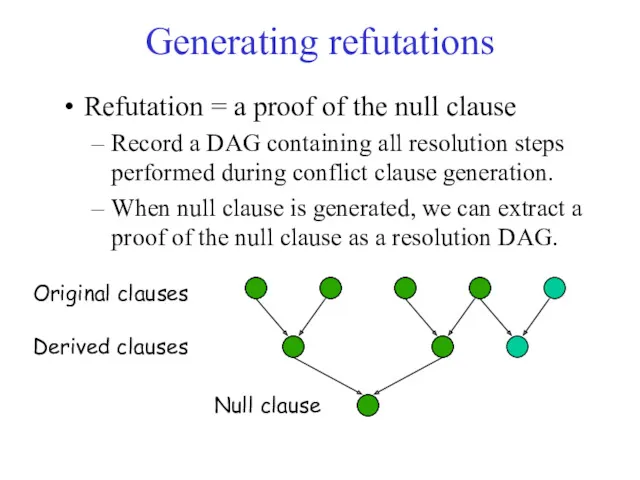
- 21. Generating refutations Refutation = a proof of the null clause Record a DAG containing all resolution
- 22. Unbounded Model Checking A variety of methods to exploit SAT and BMC for unbounded model checking:
- 23. Conclusions: BDDs vs. SAT Many models that cannot be solved by BDD symbolic model checkers, can
- 25. Скачать презентацию















 Белочка в стране Веселая математика
Белочка в стране Веселая математика Письменное сложение двузначных чисел без перехода через десяток
Письменное сложение двузначных чисел без перехода через десяток Задачи с экономическим содержанием
Задачи с экономическим содержанием Весёлая математика
Весёлая математика Решение логарифмических неравенств
Решение логарифмических неравенств Конспект урока по математике 4 класс Школа России Письменное деление
Конспект урока по математике 4 класс Школа России Письменное деление Анимашки для презентаций в Microsoft PowerPoint - 5
Анимашки для презентаций в Microsoft PowerPoint - 5 Неопределенный интеграл
Неопределенный интеграл Математика (початкова школа)
Математика (початкова школа) Презентация по математике Калькулятор
Презентация по математике Калькулятор Критерий согласия распределений χ 2
Критерий согласия распределений χ 2 Угол между прямыми
Угол между прямыми Интерактивный кроссворд: Стереометрия
Интерактивный кроссворд: Стереометрия Перестановки. Размещения. Сочетания. комбинаторика
Перестановки. Размещения. Сочетания. комбинаторика Деление десятичных дробей
Деление десятичных дробей Сложение и вычитание в пределах 10. 1 класс
Сложение и вычитание в пределах 10. 1 класс Среднее арифметическое. Деление десятичной дроби на натуральное число
Среднее арифметическое. Деление десятичной дроби на натуральное число Школа Квентин – подготовка к ЕГЭ
Школа Квентин – подготовка к ЕГЭ Математика. 1 класс. Урок 51. Число 10 - Презентация
Математика. 1 класс. Урок 51. Число 10 - Презентация прибавление и вычитание 2 и 3
прибавление и вычитание 2 и 3 Симметричные фигуры
Симметричные фигуры Численные методы алгебры
Численные методы алгебры Вычитание числа с переходом через десяток, вида 13-
Вычитание числа с переходом через десяток, вида 13- Множественная линейная регрессия
Множественная линейная регрессия Презентация к уроку математики в 4 классе по теме ПОСТРОЕНИЕ ТОЧЕК ПО ИХ КООРДИНАТАМ.
Презентация к уроку математики в 4 классе по теме ПОСТРОЕНИЕ ТОЧЕК ПО ИХ КООРДИНАТАМ. счёт в пределах 10.
счёт в пределах 10.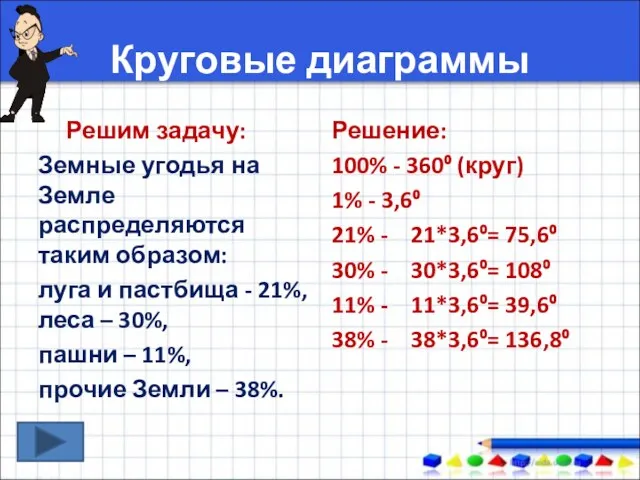 Круговые диаграммы
Круговые диаграммы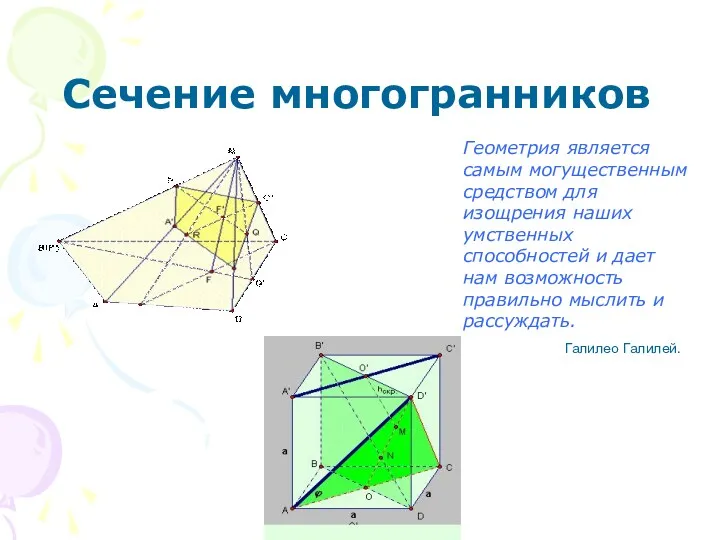 Сечение многогранников
Сечение многогранников