Приказ командира: брить тех и только тех,
кто не бреется сам.
А
= {те и только те, кто не бреется сам}
Вопрос: брадобрей ∈ А?
Другая формулировка парадокса брадобрея
Прилагательное называется рефлексивным, если оно само обладает свойством, которое определяет
Примеры рефлексивных прилагательных: «русский», «трёхсложный»
Примеры нерефлексивных прилагательных: «английский», «четырёхсложный»
Вопрос. Если В ={все рефлексивные прилагательные}, то прилагательное «нерефлексивный» ∈ В или нет?
Вопрос-шутка: «трудновыговариваемый» ∈ В или нет?
Парадокс брадобрея



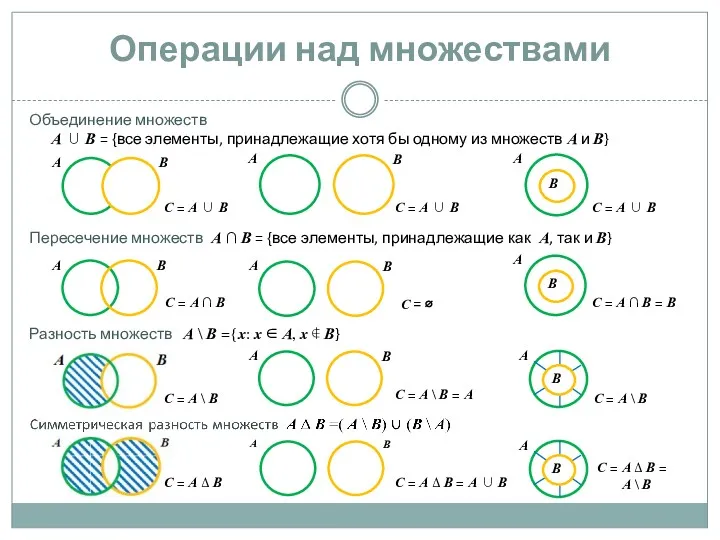

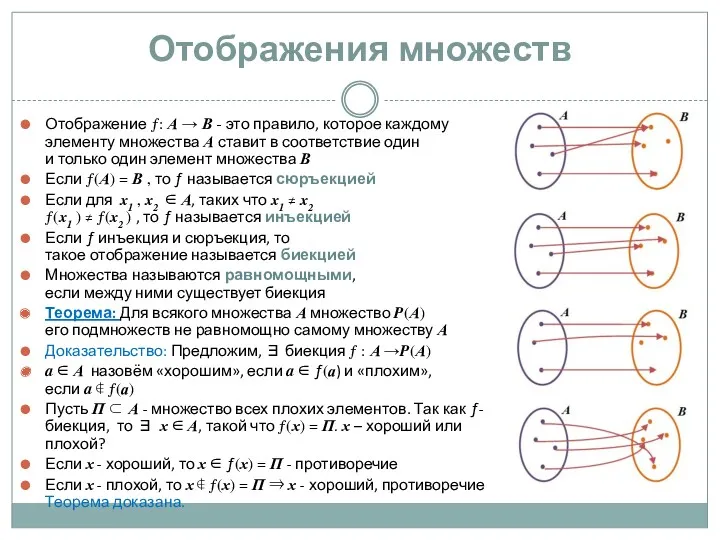

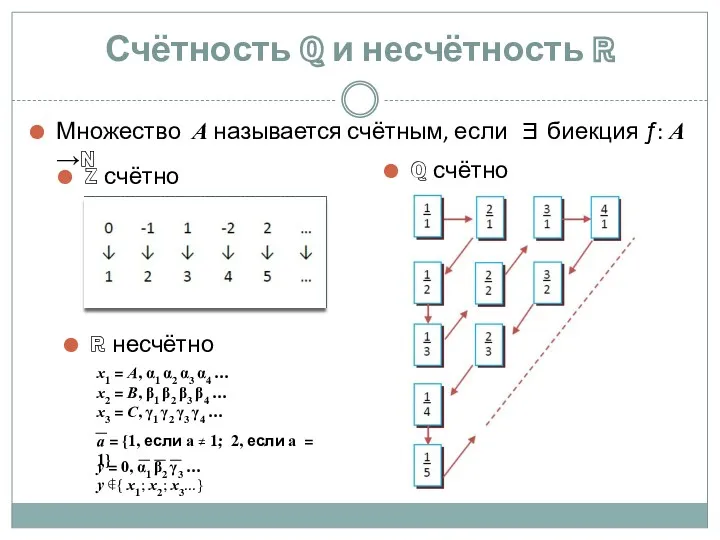

 Числовые и буквенные выражения
Числовые и буквенные выражения Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными Умножение натуральных чисел
Умножение натуральных чисел Теорема Чевы
Теорема Чевы Неделя математики
Неделя математики Симметрия в природе, технике, быту, искусстве, русском языке, математике
Симметрия в природе, технике, быту, искусстве, русском языке, математике Теорема про три перпендикуляри
Теорема про три перпендикуляри Открытый урок в 7 классе
Открытый урок в 7 классе События
События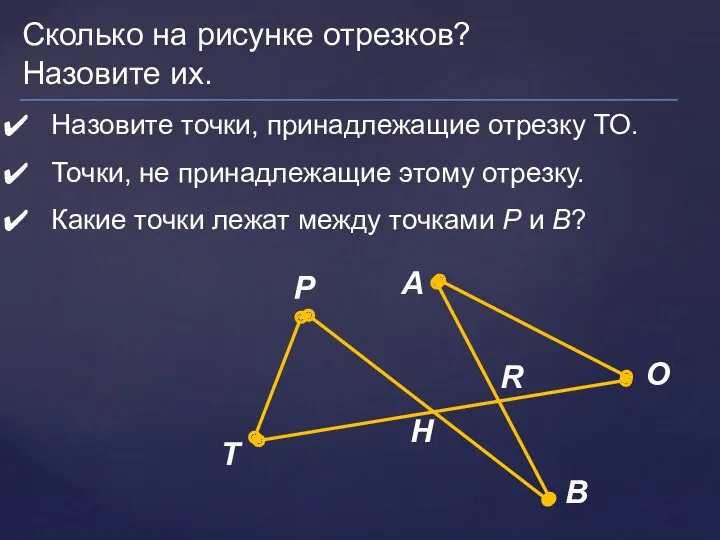 Сравнение отрезков
Сравнение отрезков Порядок выполнения действий в примерах
Порядок выполнения действий в примерах Теория информационных процессов и систем. Лекция 1. Информационный процесс
Теория информационных процессов и систем. Лекция 1. Информационный процесс Алгоритм вычитания трехзначных чисел
Алгоритм вычитания трехзначных чисел Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Задачи на построение сечений. 10 класс
Задачи на построение сечений. 10 класс Векторы в пространстве
Векторы в пространстве Раскрась флажки игра-тренажёр по математике 2 класс по теме Уравнение
Раскрась флажки игра-тренажёр по математике 2 класс по теме Уравнение Правильные многогранники
Правильные многогранники конспект урока по математике во 2 классе. УМК Перспективная начальная школа. Тема урока Периметр многоугольника.
конспект урока по математике во 2 классе. УМК Перспективная начальная школа. Тема урока Периметр многоугольника. Действия с целыми числами. 6 класс
Действия с целыми числами. 6 класс Деление на десятичную дробь. Устный счет
Деление на десятичную дробь. Устный счет Наибольший общий делитель. Взаимно простые числа. 6 класс
Наибольший общий делитель. Взаимно простые числа. 6 класс Презентация к уроку Письменное умножение на двузначное число
Презентация к уроку Письменное умножение на двузначное число Модуль числа. Противоположные числа
Модуль числа. Противоположные числа Счет предметов в пределах десяти.
Счет предметов в пределах десяти. Математический КВН
Математический КВН Алгебра логики
Алгебра логики Координатная плоскость. Обобщение и систематизация изученного материала. 6 класс
Координатная плоскость. Обобщение и систематизация изученного материала. 6 класс