Содержание
- 2. Цель работы: знакомство с различными способами решения квадратных уравнений. Задачи: изучить исторические сведения; приобрести новые знания;
- 3. Гипотеза: существуют ли другие способы решения квадратных уравнений и как они используются в современном мире. Методы
- 4. Исторические сведения Квадратные уравнения могли решать ещё 2000 лет до н.э. вавилоняне. Во всех обнаруженных текстах
- 5. Вклад математиков Диофант Брахмагупта Мухаммед аль – Хорезми
- 6. Вклад математиков Леонардо Фибоначчи Михаель Штифель Франсуа Виет
- 7. Это интересно
- 8. Учёные, изучающие квадратные уравнения Тарталья Кардано Бомбелли Жирар Ньютон Декарт
- 9. Появление значка корень √ - радикал radix – латинское «корень» r -
- 10. Квадратное уравнение и его виды Квадратное уравнение – уравнение вида ax2 + bx + c =
- 11. Способы решения квадратных уравнений Способ разложения на множители 7х2 + 9х + 2 = 0 7х2
- 12. Способы решения квадратных уравнений Способом выделения квадрата двучлена х2 +4х - 12 =0 ( х2+4х+4) -
- 13. Способы решения квадратных уравнений По теореме Виета (обратной) Для приведённого квадратного уравнения x2 + px +
- 14. Способы решения квадратных уравнений Используя свойства коэффициентов Пусть ах2 + bх + с = 0, где
- 15. Способы решения квадратных уравнений Решение по формулам Где D – дискриминант Если D Если D=0, то
- 16. Способы решения квадратных уравнений Способ переброски ах2 + bх + с = 0 Умножая обе его
- 17. Способы решения квадратных уравнений Способ переброски 2х2 + 3х – 2 = 0, умножим обе части
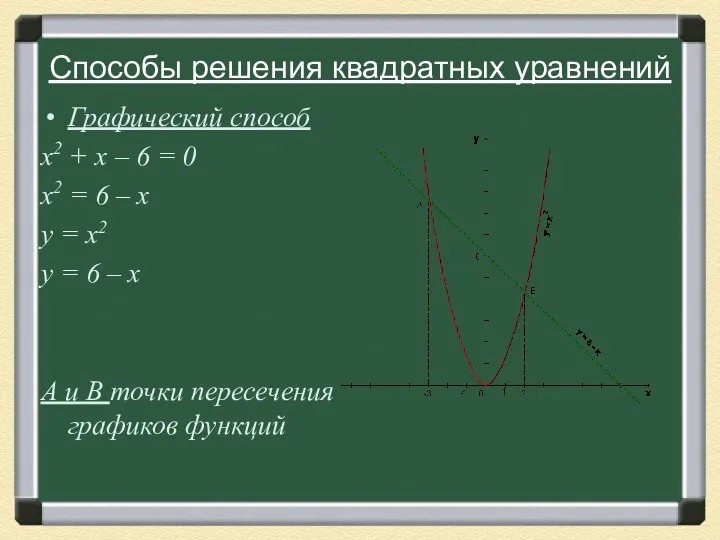
- 18. Способы решения квадратных уравнений Графический способ Если в уравнении x2 +px +q= 0 перенести второй и
- 19. Способы решения квадратных уравнений Графический способ х2 + х – 6 = 0 х2 = 6
- 20. Способы решения квадратных уравнений Графический способ С помощью программы «Advanced Grapher» Решим уравнения: 1)2х2 -9х+7=0 2)4х2
- 21. Способы решения квадратных уравнений С помощью циркуля и линейки
- 22. Корни квадратного уравнения ах²+bx+c=0 (а≠0) можно рассматривать как абсциссы точек пересечения окружности с центром Q ,
- 23. 1 случай Если QA> то окружность пересекает ось Ох в двух точках М(х1 ; 0) и
- 24. 2 случай Если QA= то окружность касается оси Ох в точке М(х1 ; 0), уравнение имеет
- 25. 3 случай Если QA
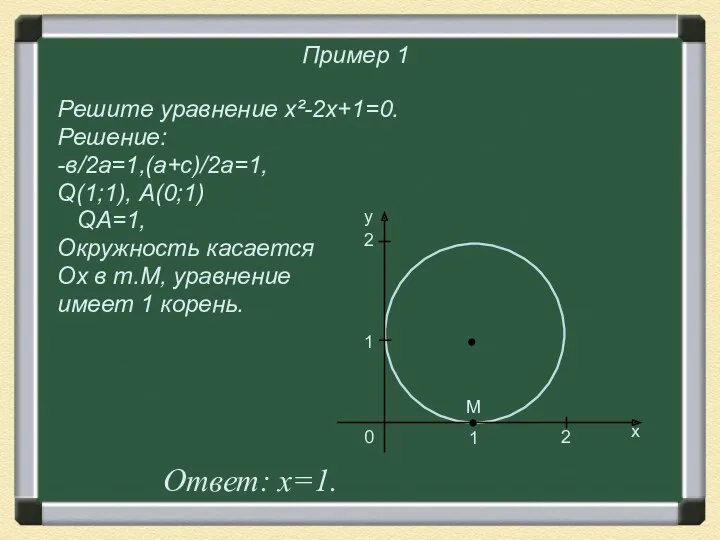
- 26. Пример 1 Решите уравнение х²-2x+1=0. Решение: -в/2а=1,(а+с)/2а=1, Q(1;1), А(0;1) QА=1, Окружность касается Ох в т.М, уравнение
- 27. Пример 2 Решите уравнение х²+4x-5=0. Решение:-в/2а=-2; (а+с)/2а=-2 Q(-2;-2),А(0;1) QА>-2,окружность пересекает ох в двух точках, уравнение имеет
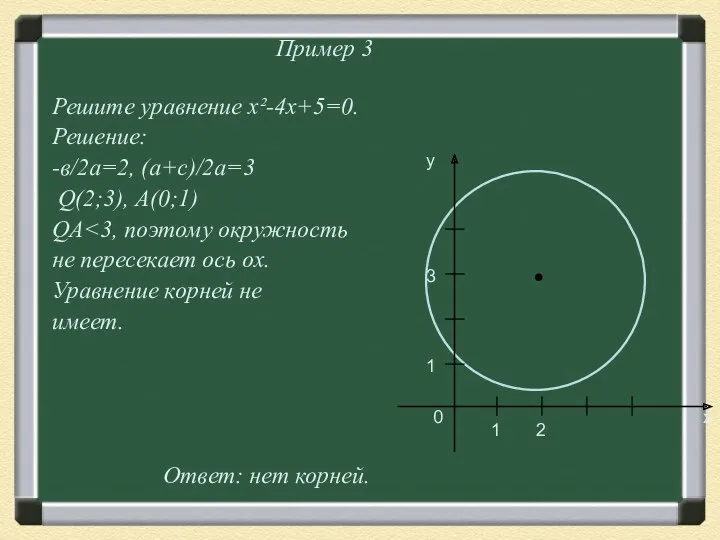
- 28. Пример 3 Решите уравнение х²-4x+5=0. Решение: -в/2а=2, (а+с)/2а=3 Q(2;3), А(0;1) QА не пересекает ось ох. Уравнение
- 29. Способы решения квадратных уравнений Использование языков программирования Program kwur; var a,b,c,d,x1,x2: real; begin write('введите коэффициенты уравнения
- 30. Заключение В процессе изучения данной темы, я ознакомилась с дополнительной литературой по истории математики, со способами
- 32. Скачать презентацию

























 Формулы косинуса суммы и разности двух аргументов. 10 класс
Формулы косинуса суммы и разности двух аргументов. 10 класс Есептерді салыстыру
Есептерді салыстыру Призма и ее виды. Сечения призм
Призма и ее виды. Сечения призм Порядок выполнения действий в выражениях (математика, 3 класс, УМК Гармония).
Порядок выполнения действий в выражениях (математика, 3 класс, УМК Гармония). Цилиндр. Площадь его поверхности
Цилиндр. Площадь его поверхности Презентация урока-сказки по математике, тема Связь умножения и деления, 3 класс
Презентация урока-сказки по математике, тема Связь умножения и деления, 3 класс Практикум №2 по решению стереометрических задач (базовый уровень)
Практикум №2 по решению стереометрических задач (базовый уровень) Приближенные значения действительных чисел
Приближенные значения действительных чисел Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3)
Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3)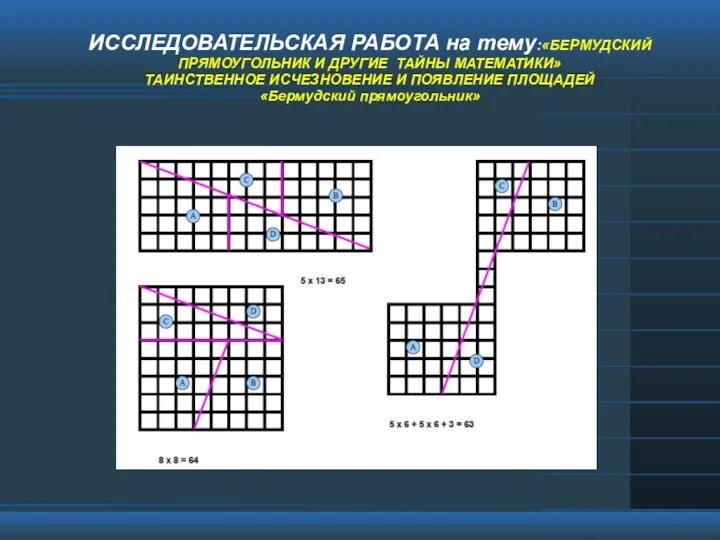 Бермудский прямоугольник и другие тайны математики, таинственное исчезновение и появление площадей
Бермудский прямоугольник и другие тайны математики, таинственное исчезновение и появление площадей Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Равнобедренный треугольник
Равнобедренный треугольник Формулы сокращенного умнажения
Формулы сокращенного умнажения Урок математики в 3 классе УМК Планета знаний
Урок математики в 3 классе УМК Планета знаний Кривые второго порядка
Кривые второго порядка А. С. Пушкин и математика. Совет мудрецов
А. С. Пушкин и математика. Совет мудрецов Решение показательных уравнений
Решение показательных уравнений Тренажёр-раскраска по таблице умножения
Тренажёр-раскраска по таблице умножения Вписанные и описанные окружности
Вписанные и описанные окружности волшебная полянка 1
волшебная полянка 1 Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Теория вероятностей; геометрическая вероятность; неравенство Чебышева
Теория вероятностей; геометрическая вероятность; неравенство Чебышева Сложение и вычетание двузначные чисел
Сложение и вычетание двузначные чисел Элементы комбинаторики: перестановки, сочетания и размещения
Элементы комбинаторики: перестановки, сочетания и размещения Построение сечений многогранников
Построение сечений многогранников Скорость движения
Скорость движения Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс