Содержание
- 2. ИГРА «НАЗОВИ ФИГУРУ»
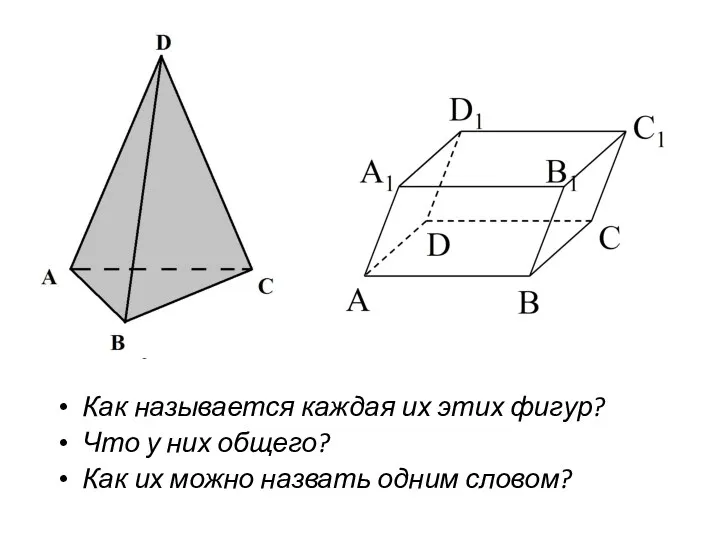
- 4. Как называется каждая их этих фигур? Что у них общего? Как их можно назвать одним словом?
- 5. МНОГОГРАННИКИ .
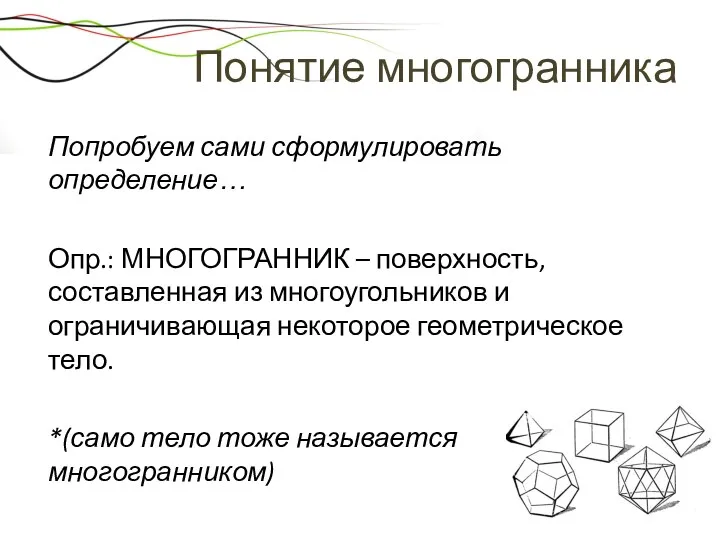
- 6. Понятие многогранника Попробуем сами сформулировать определение… Опр.: МНОГОГРАННИК – поверхность, составленная из многоугольников и ограничивающая некоторое
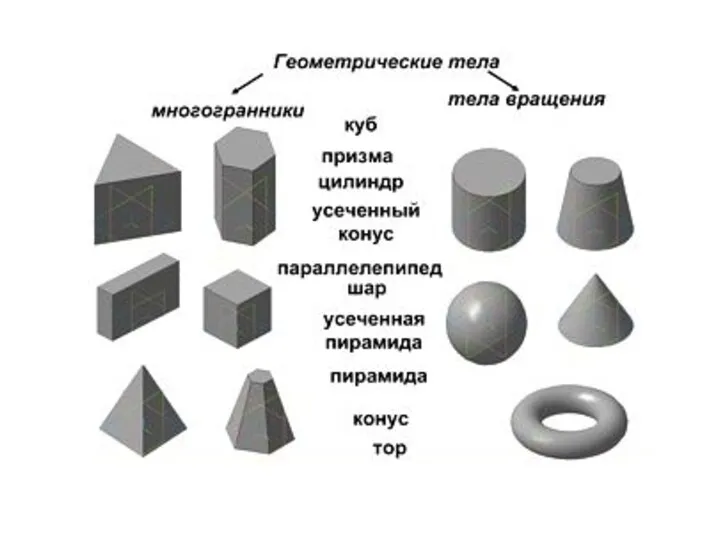
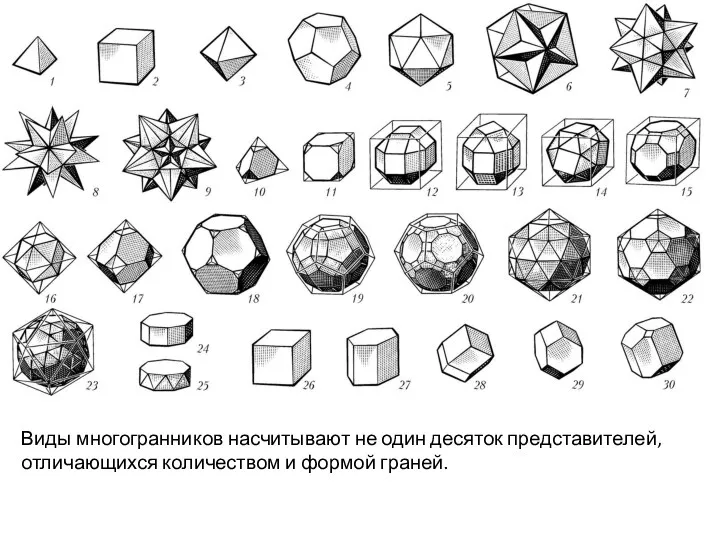
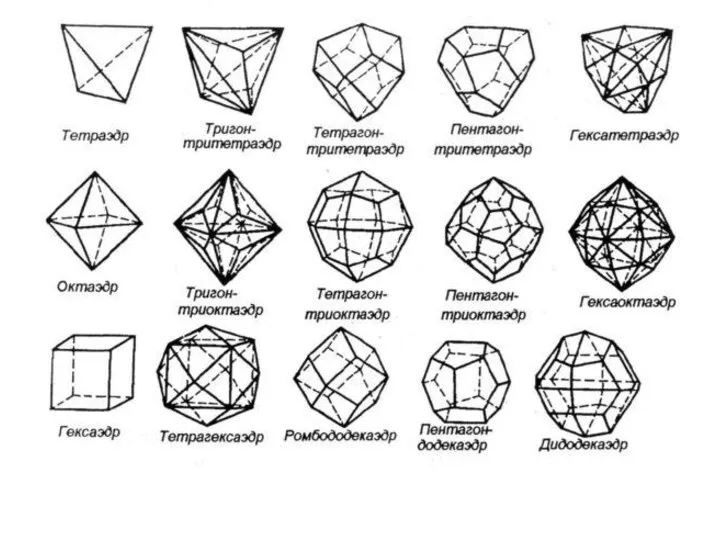
- 7. Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.
- 9. Многогранники делятся на: Выпуклые Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой
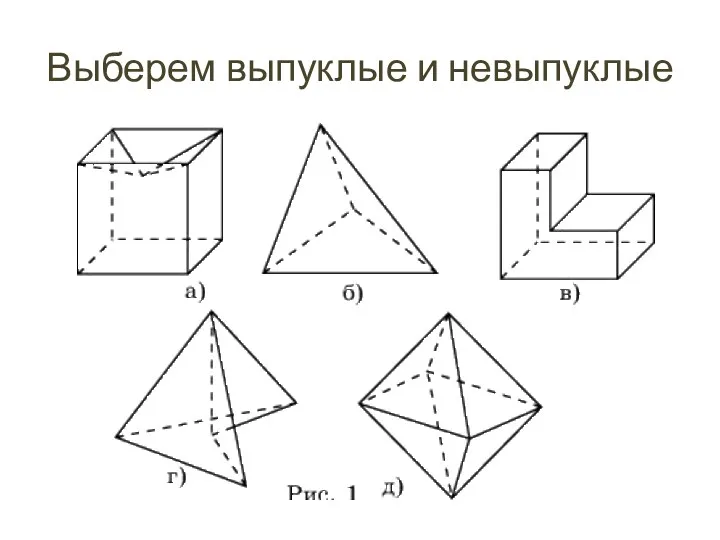
- 10. Выберем выпуклые и невыпуклые
- 11. Общие свойства многогранников: Все они имеют 3 неотъемлемых компонента: грани – многоугольники, из которых составлен многогранник;
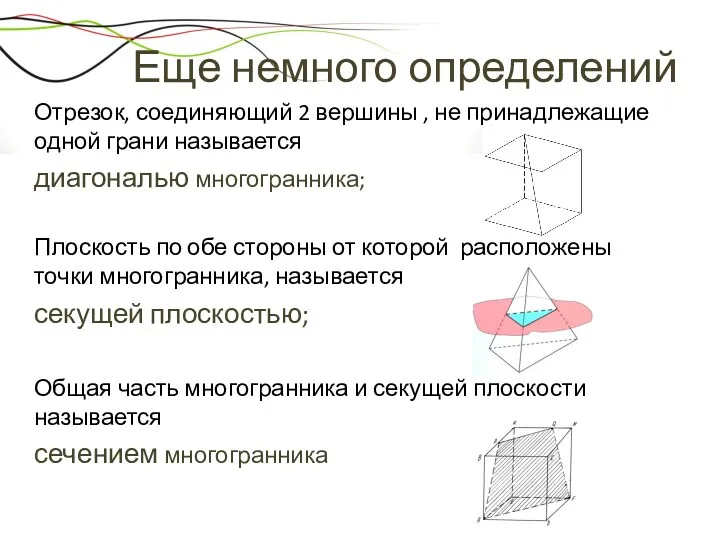
- 12. Еще немного определений Отрезок, соединяющий 2 вершины , не принадлежащие одной грани называется диагональю многогранника; Плоскость
- 13. Теорема Эйлера Леонард Эйлер (1707 - 1783) Th: В любом выпуклом многограннике сумма числа граней и
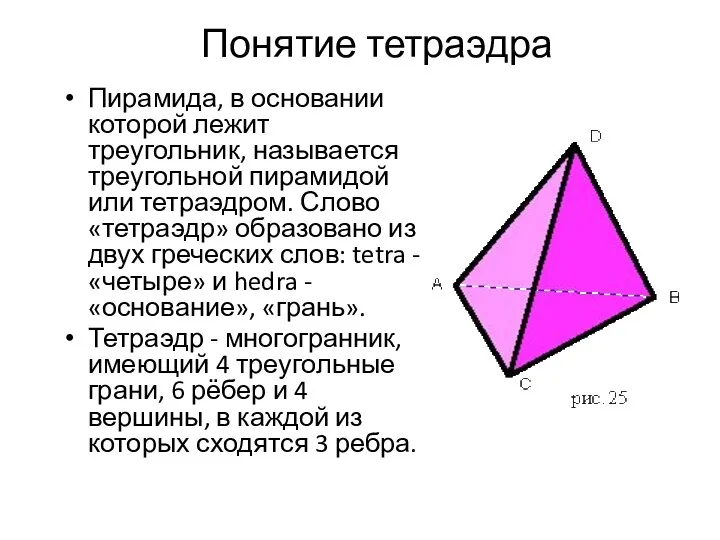
- 14. Понятие тетраэдра Пирамида, в основании которой лежит треугольник, называется треугольной пирамидой или тетраэдром. Слово «тетраэдр» образовано
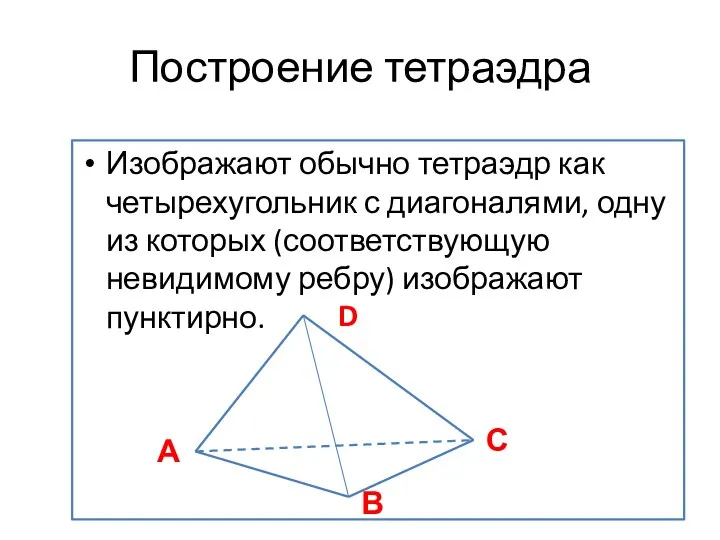
- 15. Построение тетраэдра Изображают обычно тетраэдр как четырехугольник с диагоналями, одну из которых (соответствующую невидимому ребру) изображают
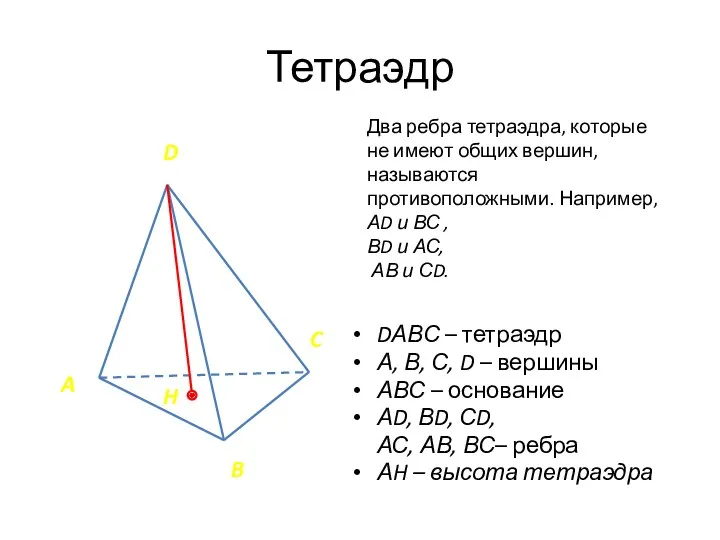
- 16. Тетраэдр DАВС – тетраэдр А, В, С, D – вершины АВС – основание АD, ВD, СD,
- 17. ПРИЗМА
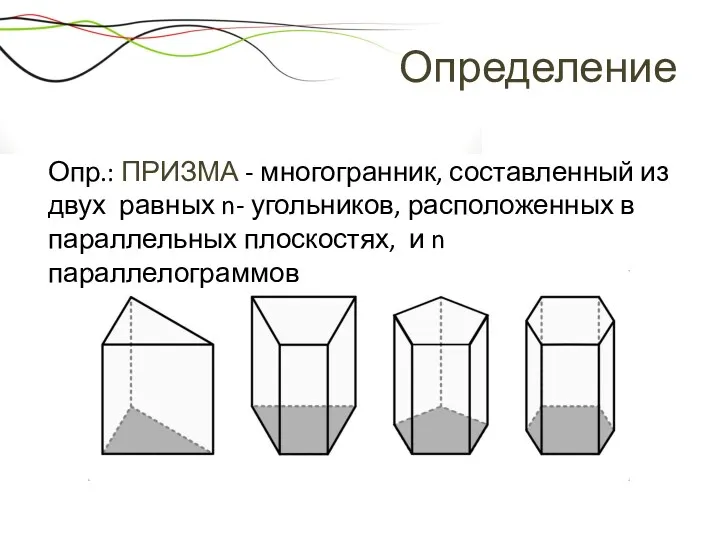
- 18. Определение Опр.: ПРИЗМА - многогранник, составленный из двух равных n- угольников, расположенных в параллельных плоскостях, и
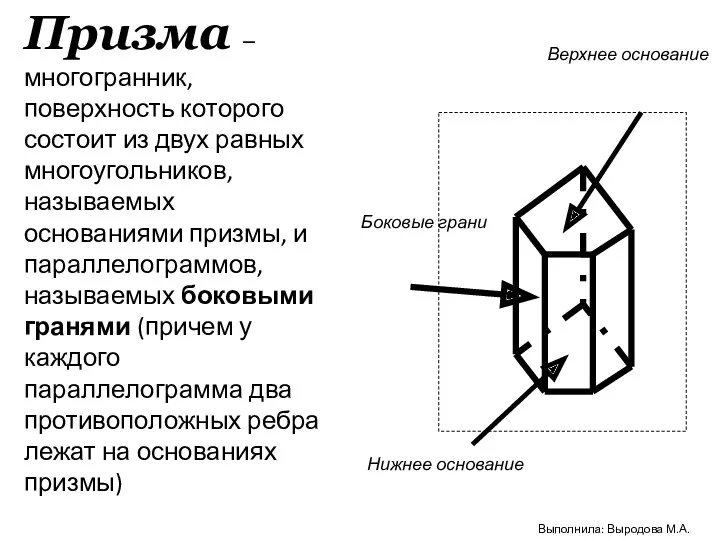
- 19. Призма – многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов, называемых
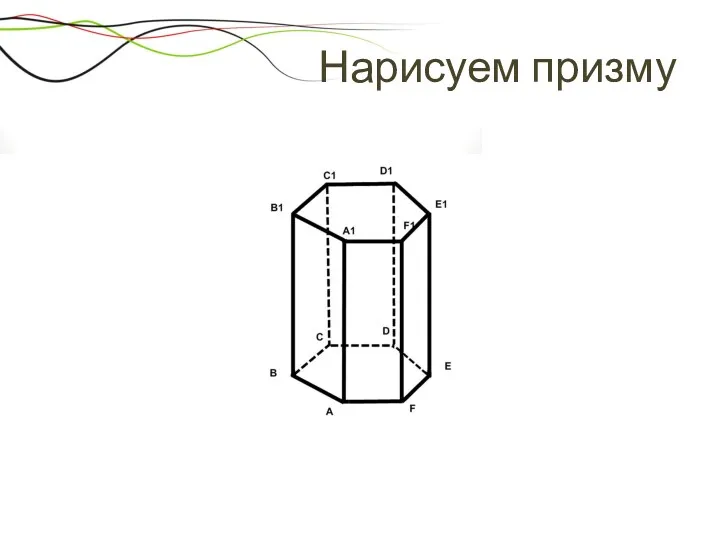
- 20. Нарисуем призму
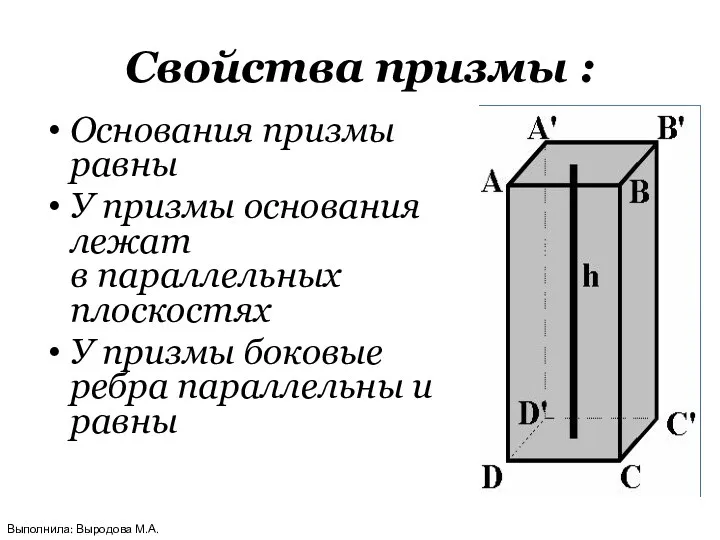
- 21. Свойства призмы : Основания призмы равны У призмы основания лежат в параллельных плоскостях У призмы боковые
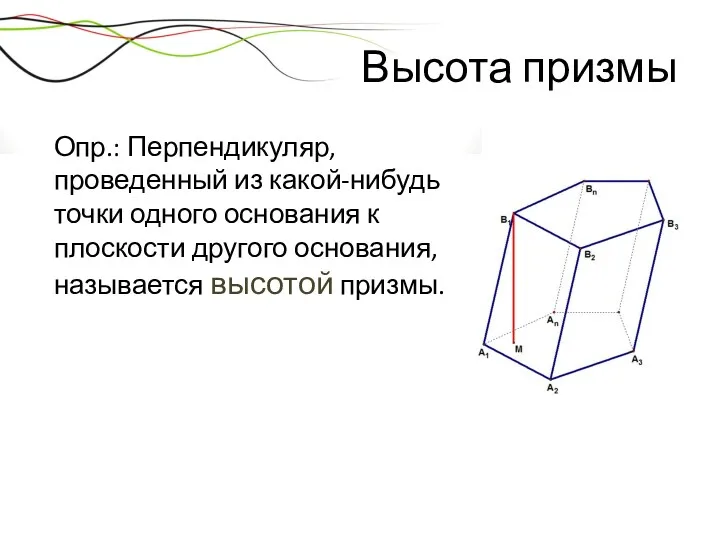
- 22. Высота призмы Опр.: Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой
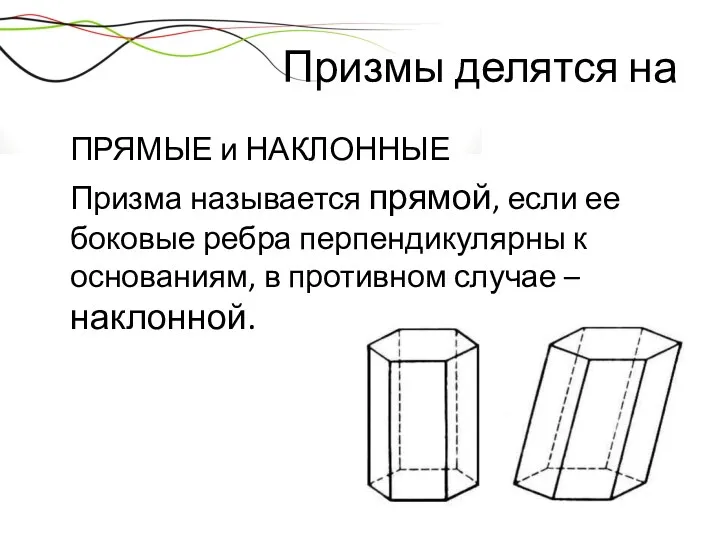
- 23. Призмы делятся на ПРЯМЫЕ и НАКЛОННЫЕ Призма называется прямой, если ее боковые ребра перпендикулярны к основаниям,
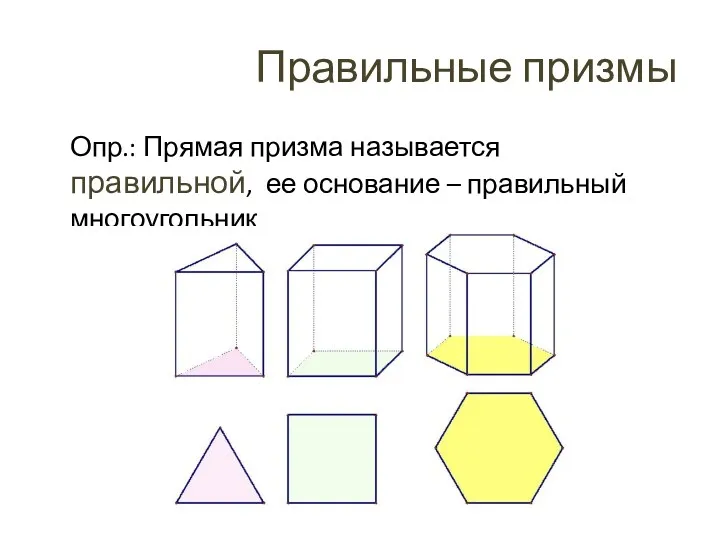
- 24. Правильные призмы Опр.: Прямая призма называется правильной, ее основание – правильный многоугольник
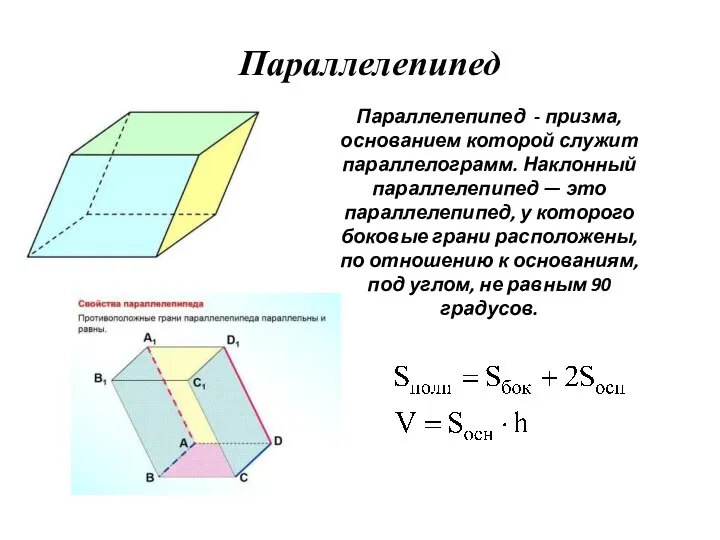
- 25. Параллелепипед Параллелепипед - призма, основанием которой служит параллелограмм. Наклонный параллелепипед — это параллелепипед, у которого боковые
- 26. Прямоугольный параллелепипед Прямоугольный параллелепипед – это такой прямой параллелепипед, у которого все грани являются прямоугольниками.
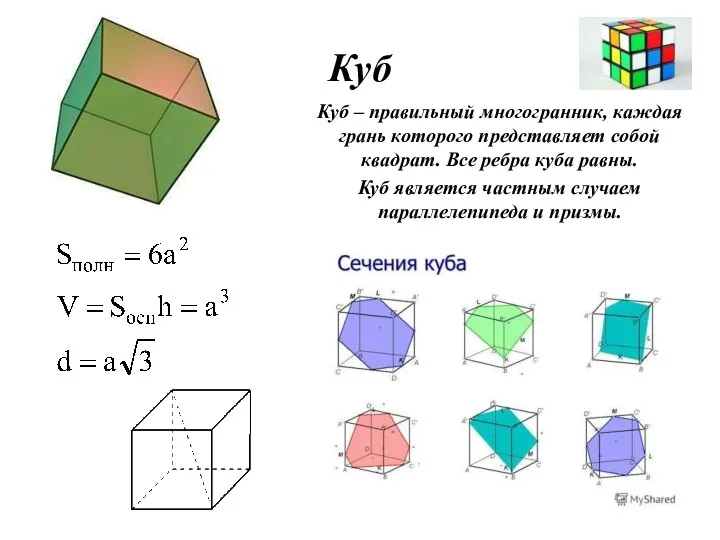
- 27. Куб Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб
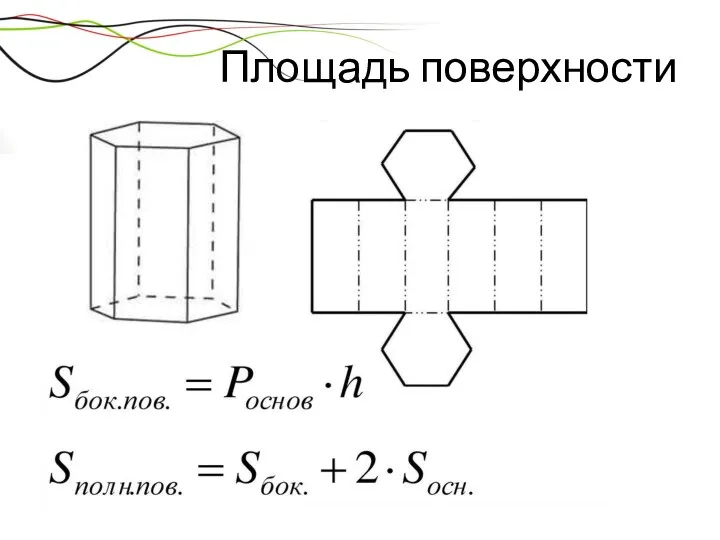
- 28. Площадь поверхности
- 29. ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ
- 30. Многие художники, искажая законы перспективы, рисуют необычные картины. Кстати, эти рисунки очень популярны среди математиков. В
- 31. Жос де Мей "Такое может нарисовать только тот, кто делает дизайн, не зная перспективы..."
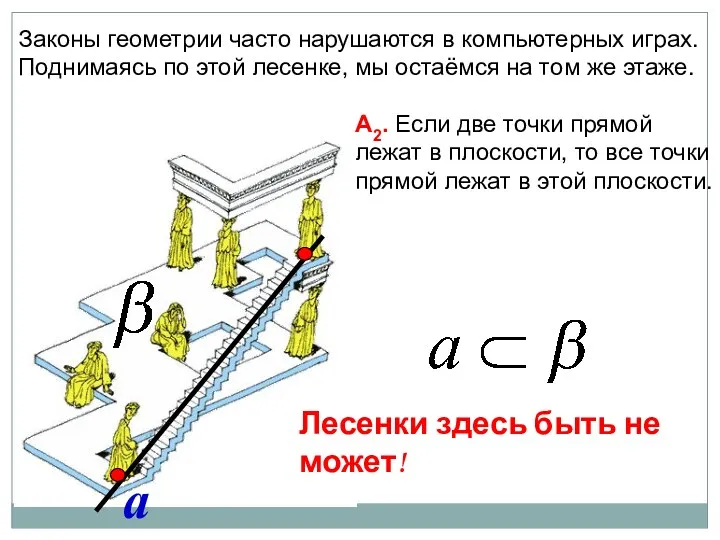
- 32. Законы геометрии часто нарушаются в компьютерных играх. Поднимаясь по этой лесенке, мы остаёмся на том же
- 33. "Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса
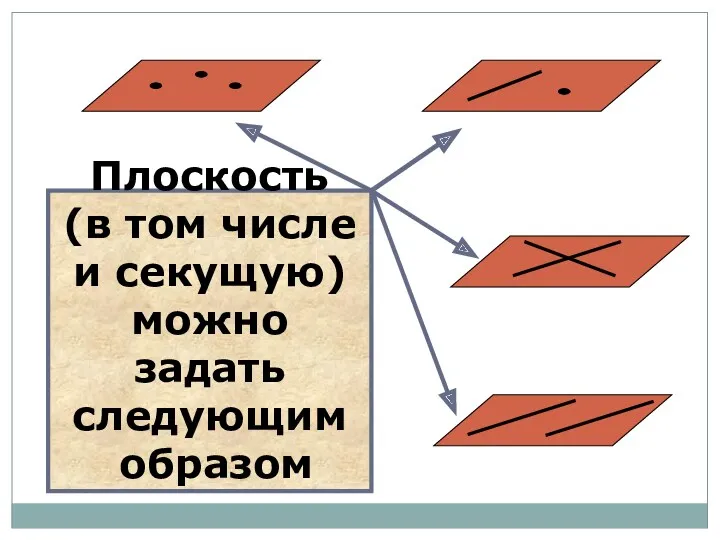
- 34. Плоскость (в том числе и секущую) можно задать следующим образом
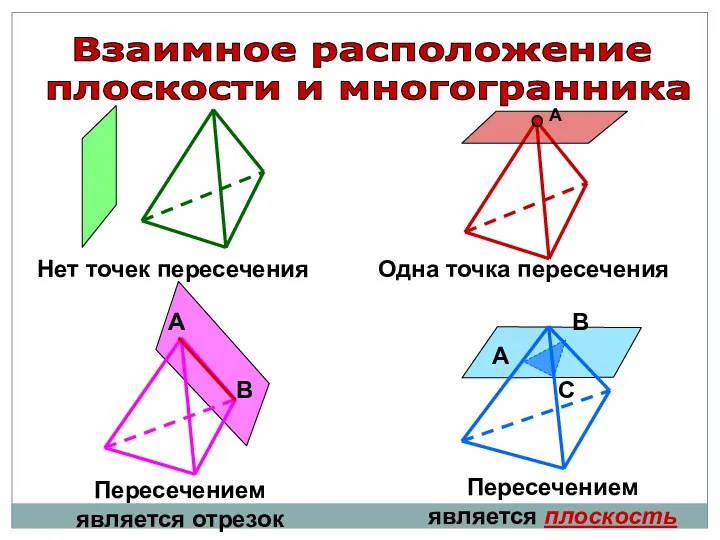
- 35. Взаимное расположение плоскости и многогранника В А Нет точек пересечения Одна точка пересечения Пересечением является отрезок
- 36. Определения. 1.Секущая плоскость тетраэдра(параллепипеда)-это любая плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллепипеда).
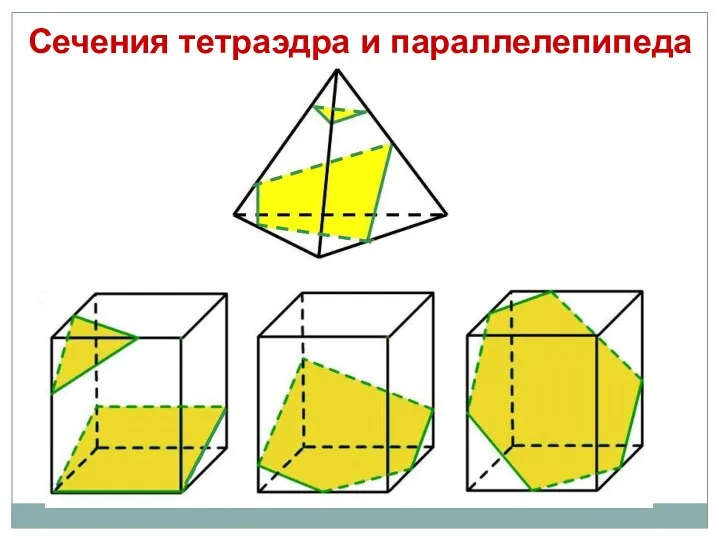
- 37. Сечения тетраэдра и параллелепипеда
- 38. Построить сечение многогранника плоскостью – это значит указать точки пересечения секущей плоскости с ребрами многогранника и
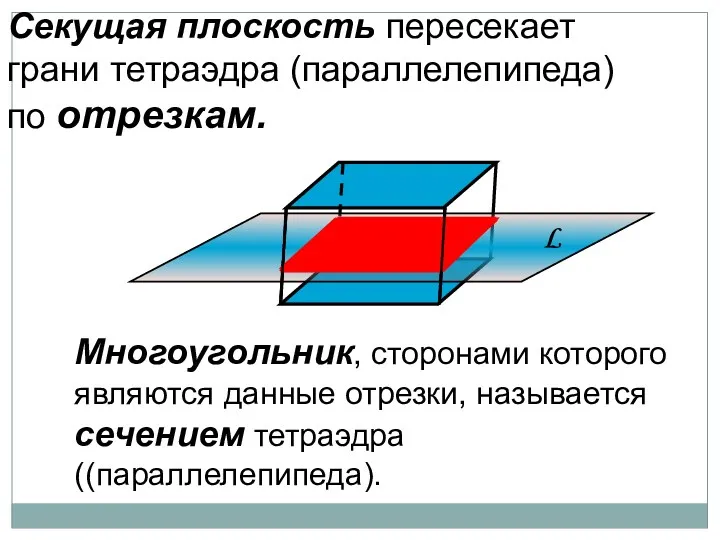
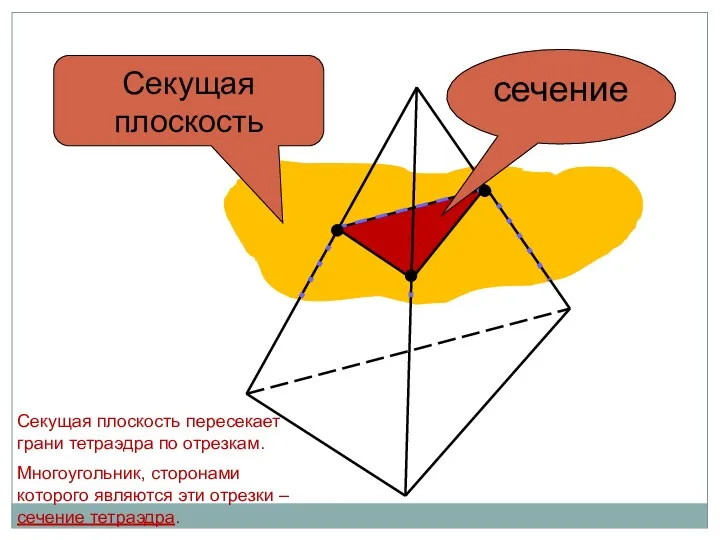
- 39. Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам. Многоугольник, сторонами которого являются данные отрезки, называется сечением
- 40. Секущая плоскость сечение Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки
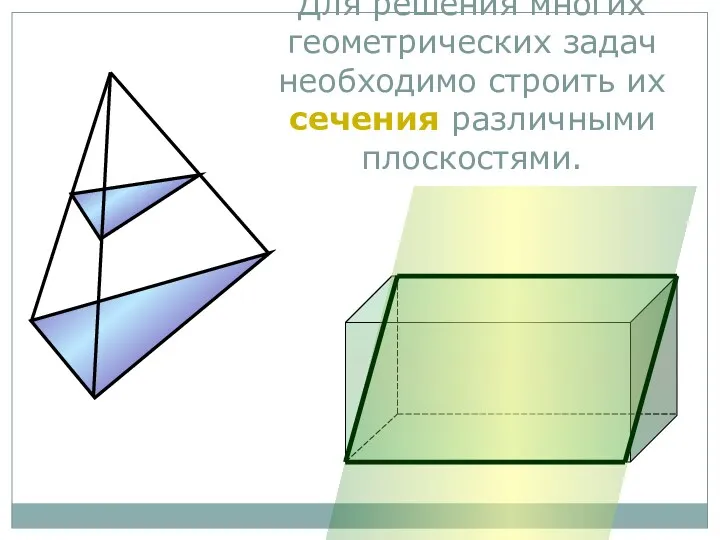
- 41. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.
- 42. АКСИОМЫ планиметрия стереометрия 1. Каждой прямой принадлежат по крайней мере две точки 2. Имеются по крайней
- 43. При этом необходимо учитывать следующее: 1. Соединять можно только две точки, лежащие в плоскости одной грани.
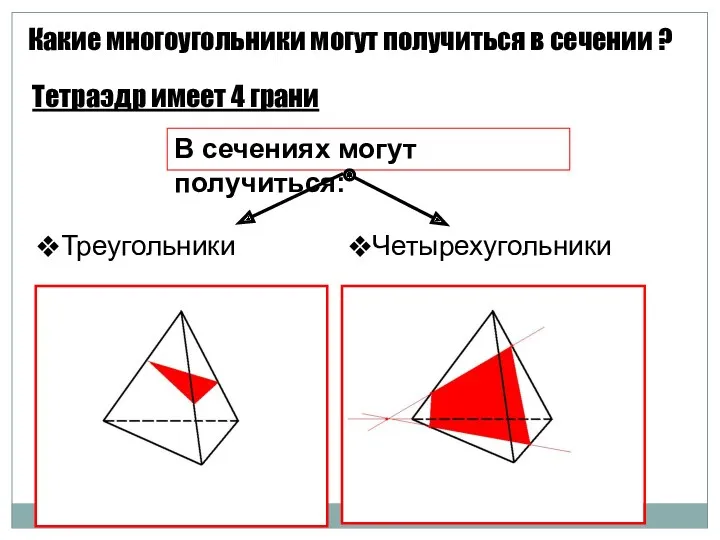
- 44. Какие многоугольники могут получиться в сечении ? Тетраэдр имеет 4 грани В сечениях могут получиться: Четырехугольники
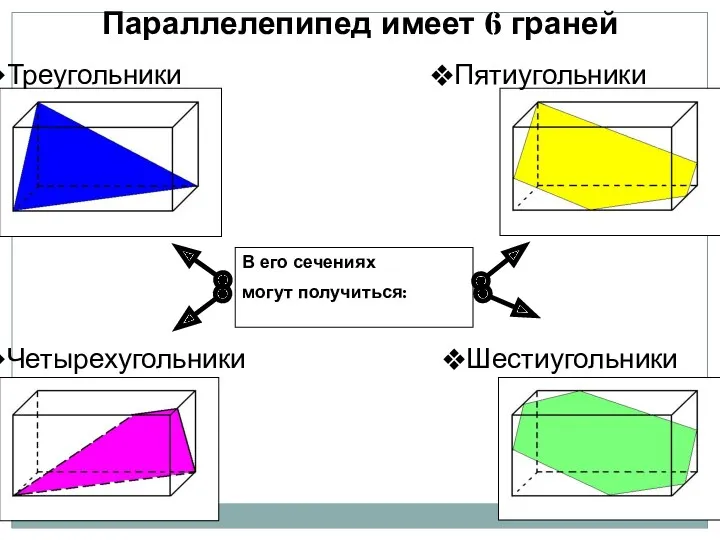
- 45. Треугольники Параллелепипед имеет 6 граней Четырехугольники Шестиугольники Пятиугольники В его сечениях могут получиться:
- 46. Блиц - опрос Задача блиц – опроса: ответить на вопросы и обосновать ответ с помощью аксиом,
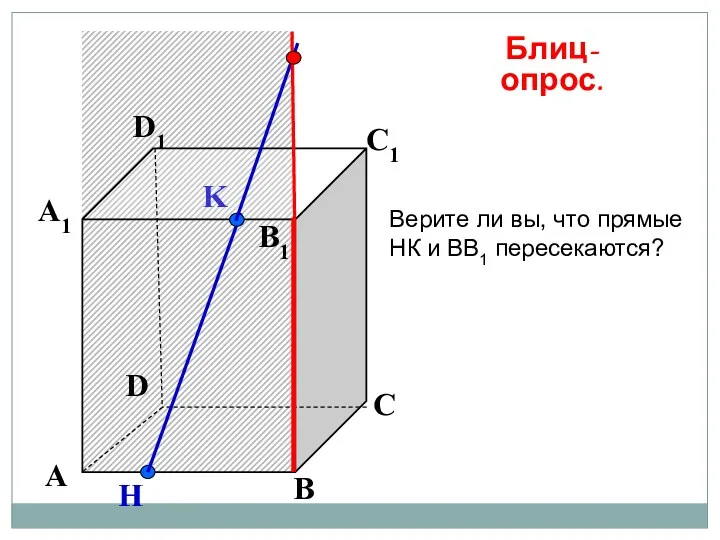
- 47. K А В С D А1 D1 С1 B1 H Блиц-опрос. Верите ли вы, что прямые
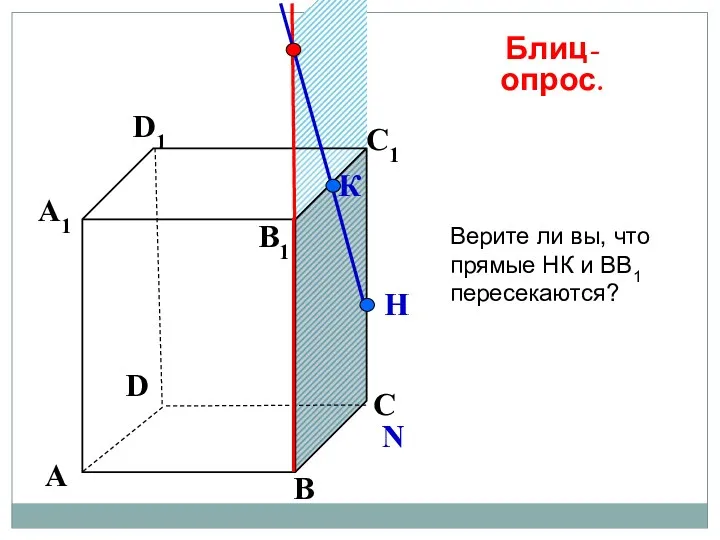
- 48. А В С D А1 D1 С1 B1 N К Н Блиц-опрос. Верите ли вы, что
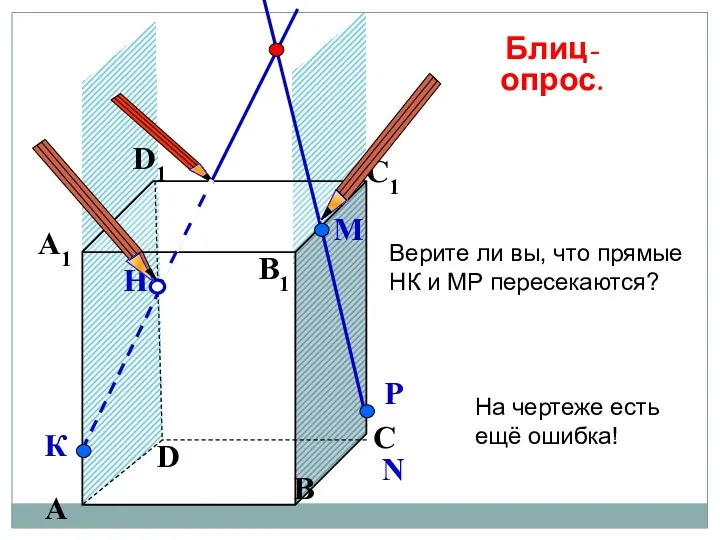
- 49. А В С D А1 D1 С1 B1 Верите ли вы, что прямые НК и МР
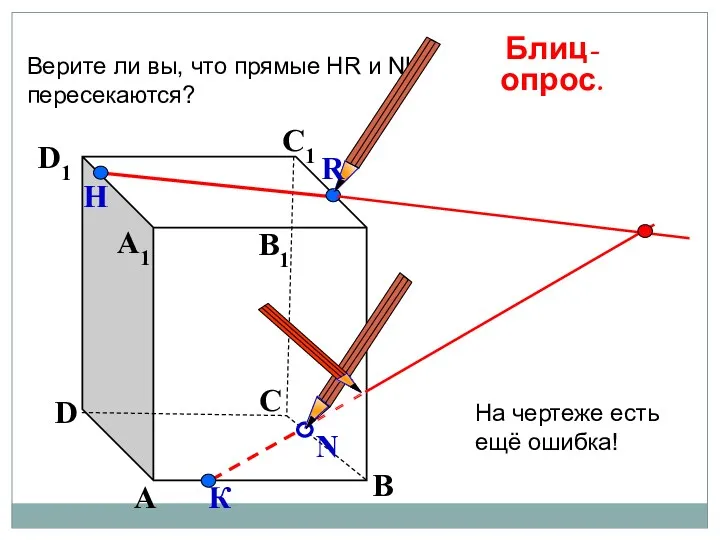
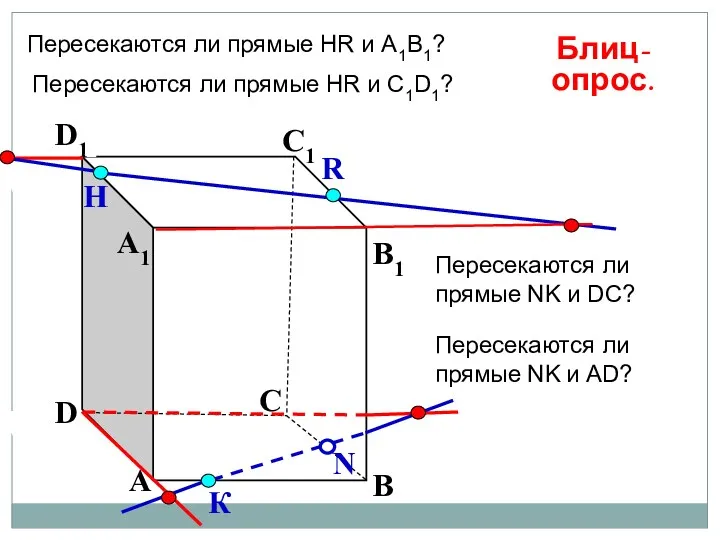
- 50. А В С D А1 D1 С1 B1 Верите ли вы, что прямые НR и NK
- 51. А В С D А1 D1 С1 B1 Пересекаются ли прямые НR и А1В1? N Н
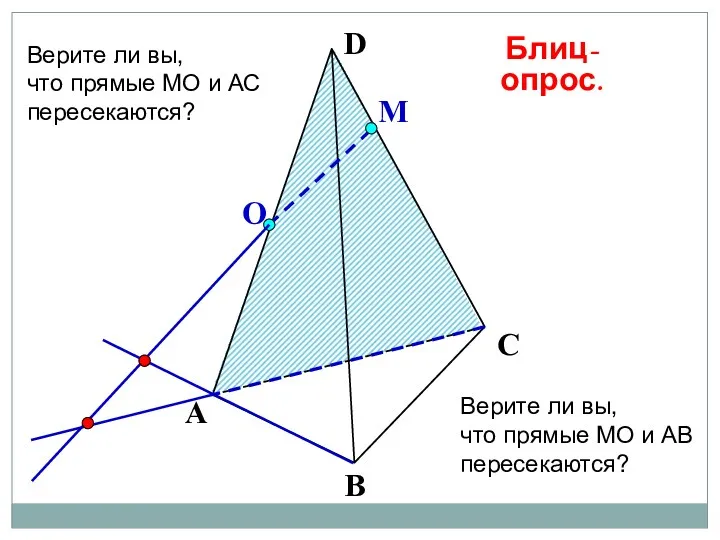
- 52. О М А В С D Верите ли вы, что прямые МО и АС пересекаются? Блиц-опрос.
- 53. Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах … : научиться этому
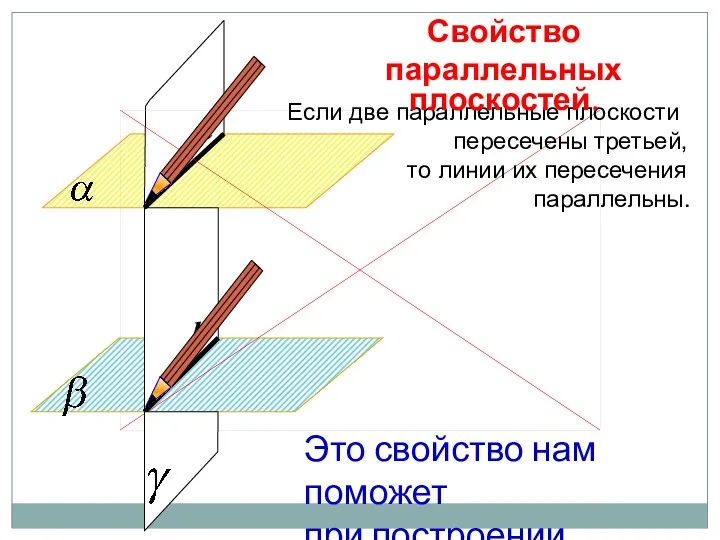
- 54. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Свойство параллельных плоскостей. Это свойство
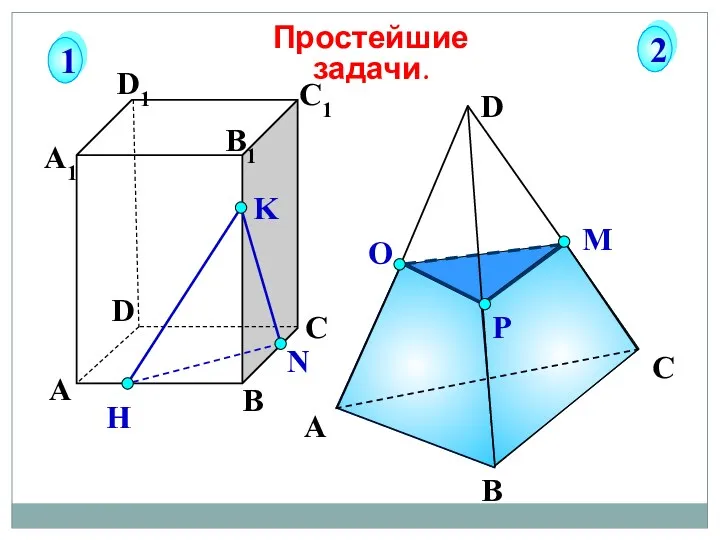
- 55. А В С D А1 D1 С1 B1 N H K Простейшие задачи. 1 2
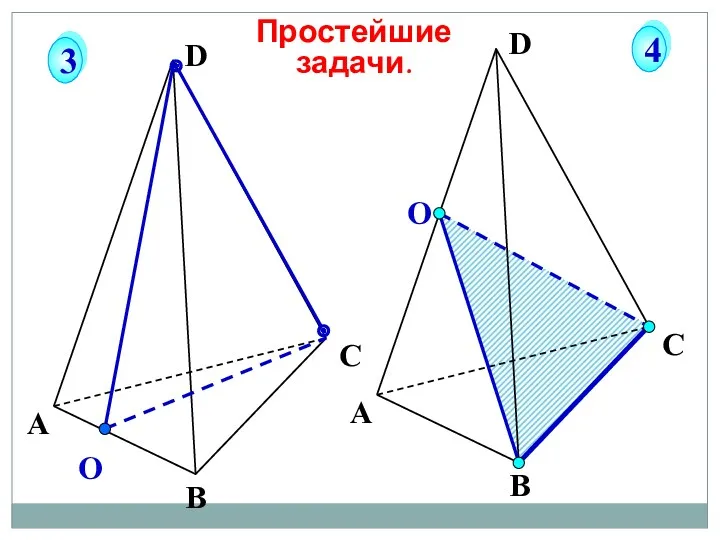
- 56. О А В С D Простейшие задачи. 3 4 О А В С D
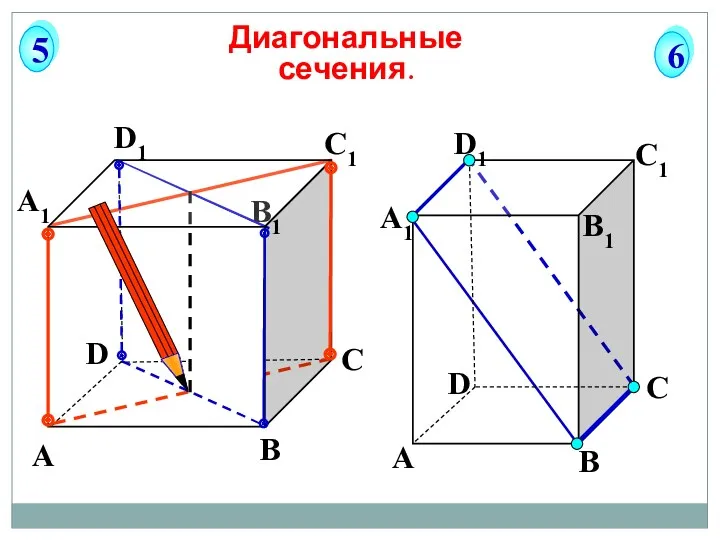
- 57. А В С D А1 D1 С1 B1 Диагональные сечения. 5 6
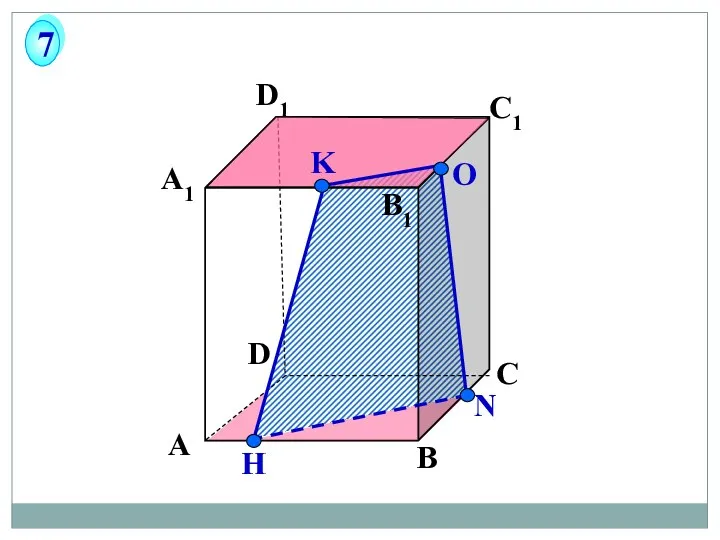
- 58. А В С D А1 D1 С1 B1 N H О 7 K
- 59. Аксиоматический метод Метод следов Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей
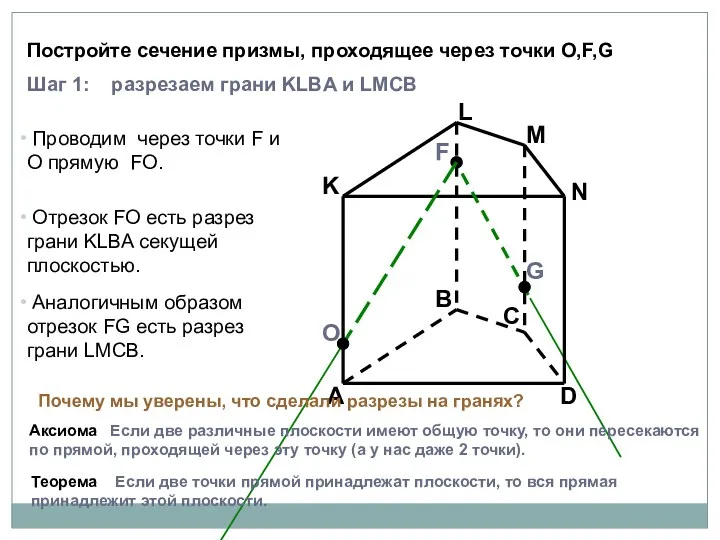
- 60. A B C D K L M N F G Проводим через точки F и O
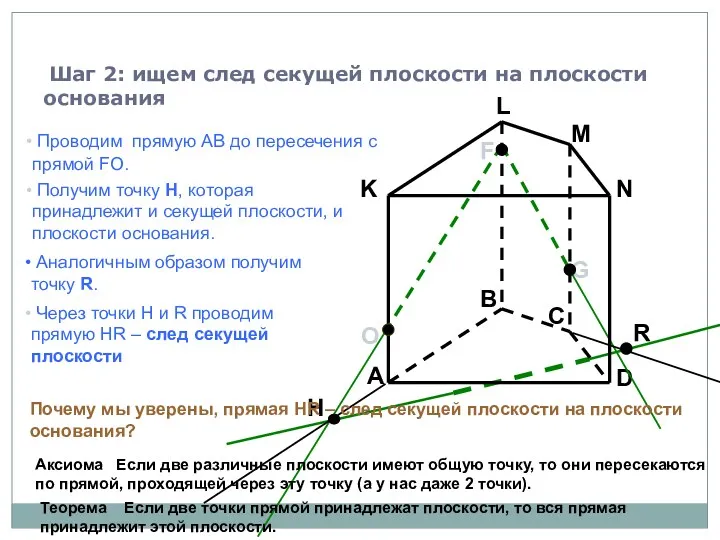
- 61. A B C D K L M N F G Шаг 2: ищем след секущей плоскости
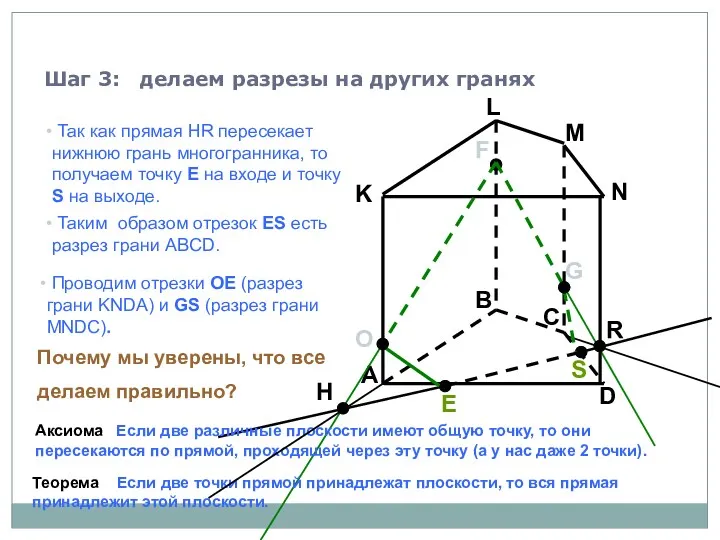
- 62. A B C D K L M N F G Шаг 3: делаем разрезы на других
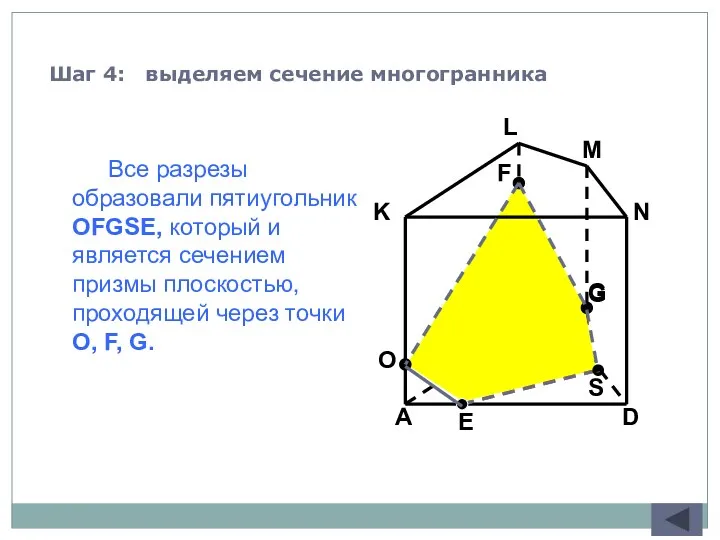
- 63. C B A D K L M N F G Шаг 4: выделяем сечение многогранника Все
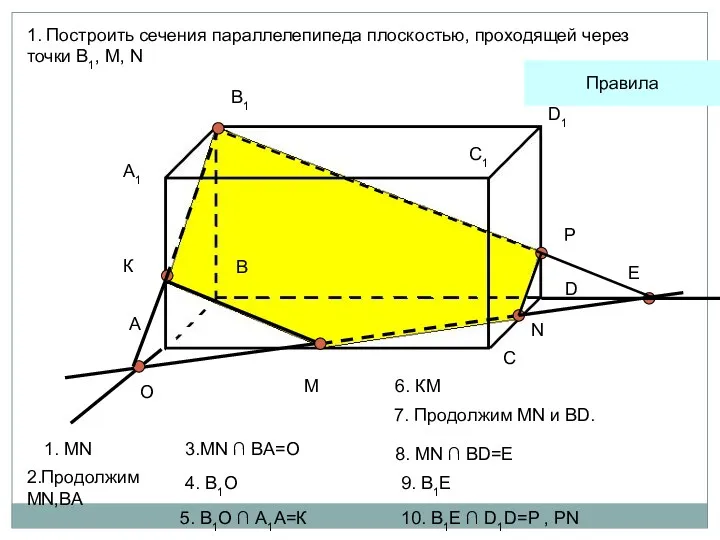
- 64. A1 А В В1 С С1 D D1 M N 1. Построить сечения параллелепипеда плоскостью, проходящей
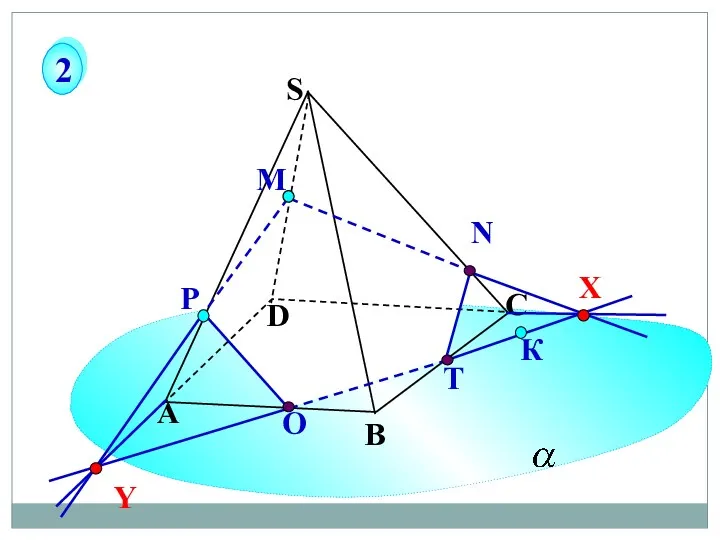
- 65. Р О Т А В С S D К М 2 X
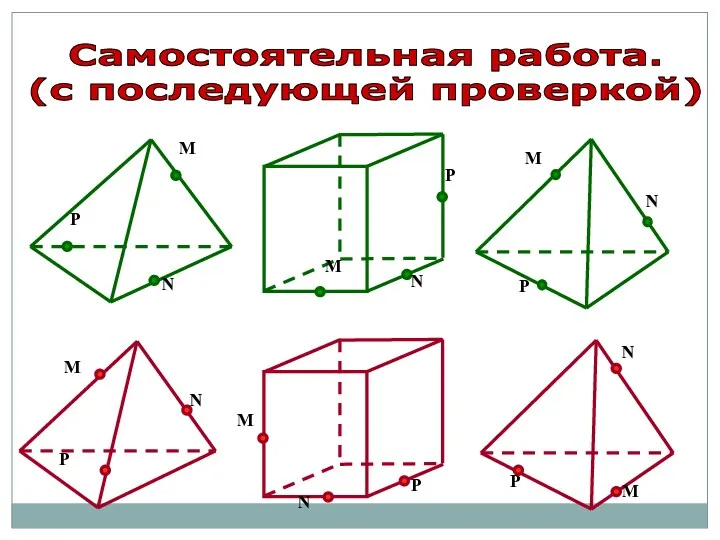
- 66. Самостоятельная работа. (с последующей проверкой)
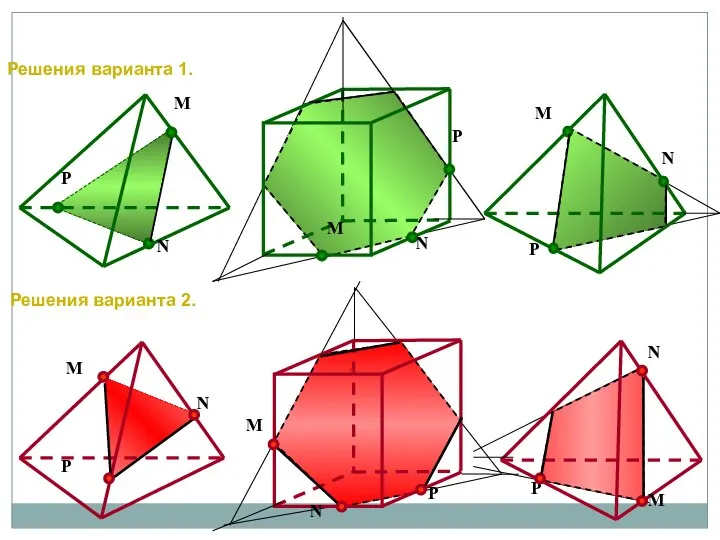
- 67. P N M N P M N P M Решения варианта 1. Решения варианта 2. M
- 68. Правила для самоконтроля: Вершины сечения находятся только на ребрах. Стороны сечения находятся только на грани многогранника.
- 69. Составить две задачи на построение сечений многогранников с использованием полученных знаний. Творческое домашнее задание
- 70. Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи,
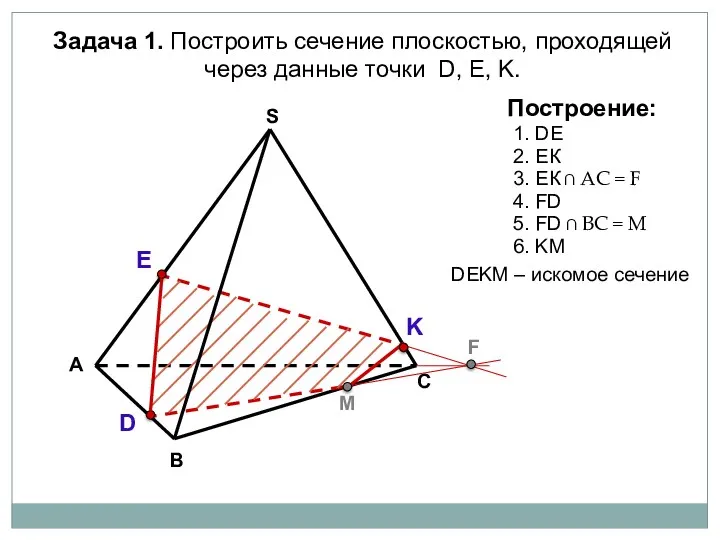
- 71. А В С S Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K.
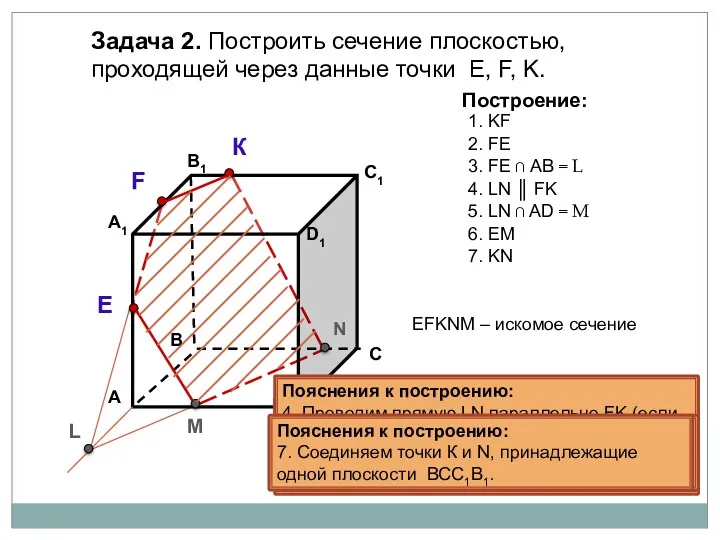
- 72. Пояснения к построению: 1. Соединяем точки K и F, принадлежащие одной плоскости А1В1С1D1. Задача 2. Построить
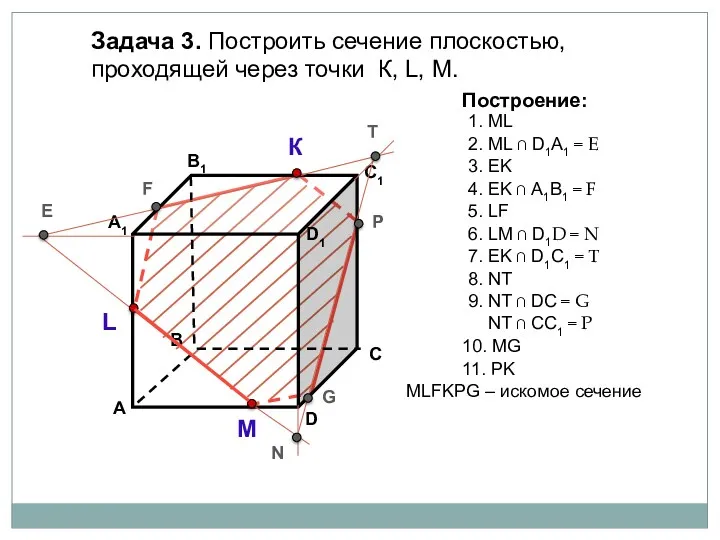
- 73. Задача 3. Построить сечение плоскостью, проходящей через точки К, L, М. К L М Построение: 1.
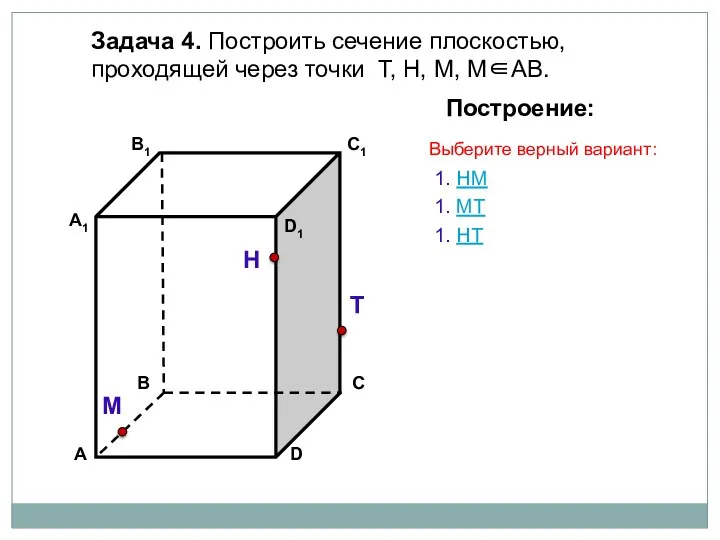
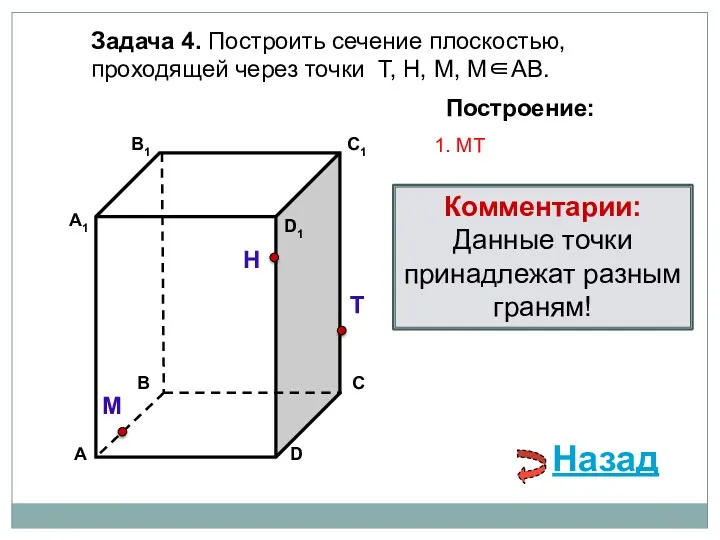
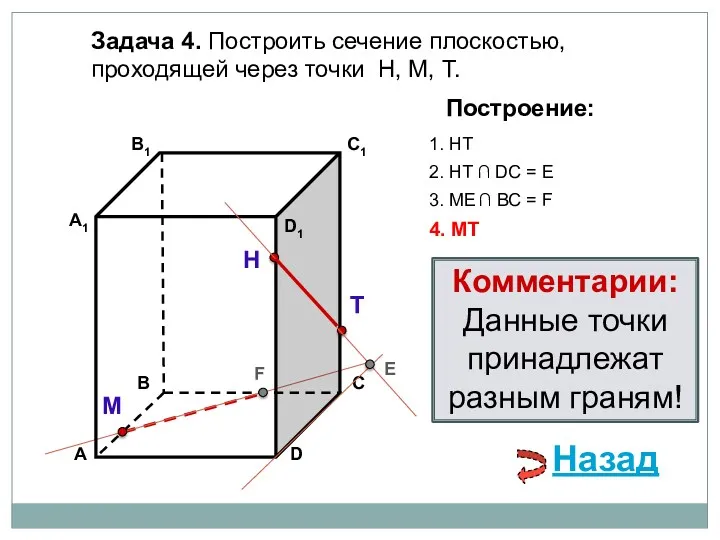
- 74. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
- 75. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
- 76. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
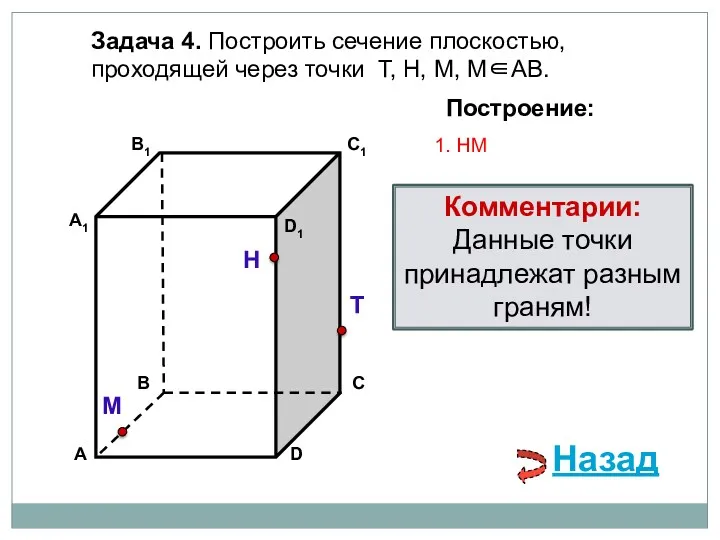
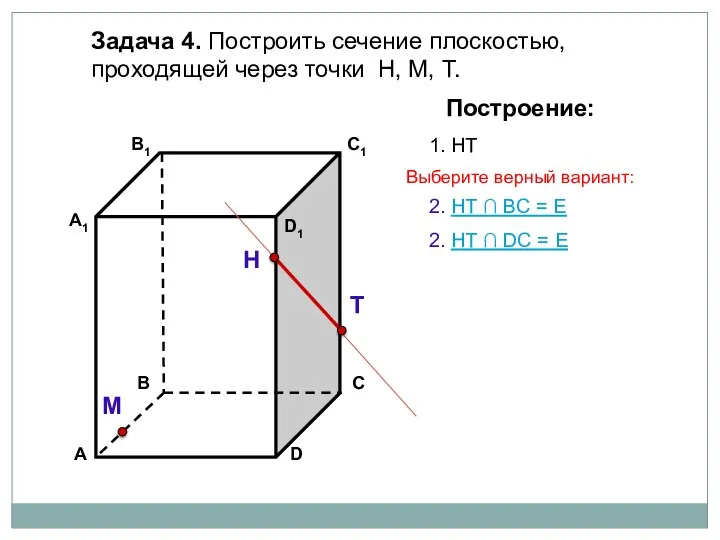
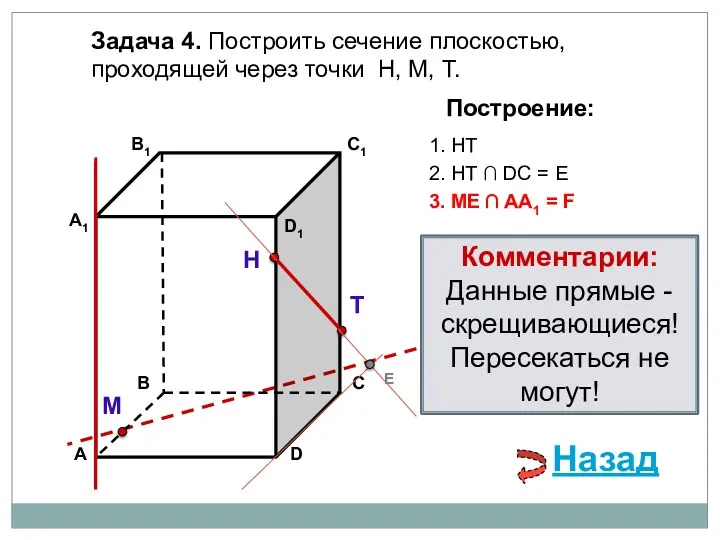
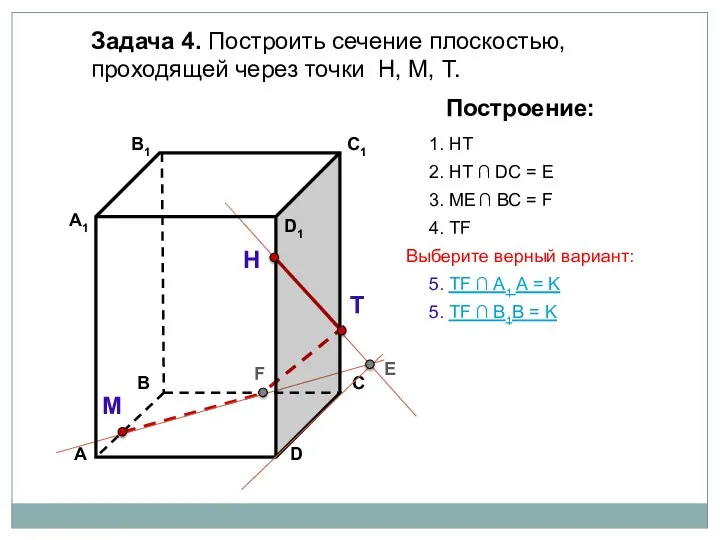
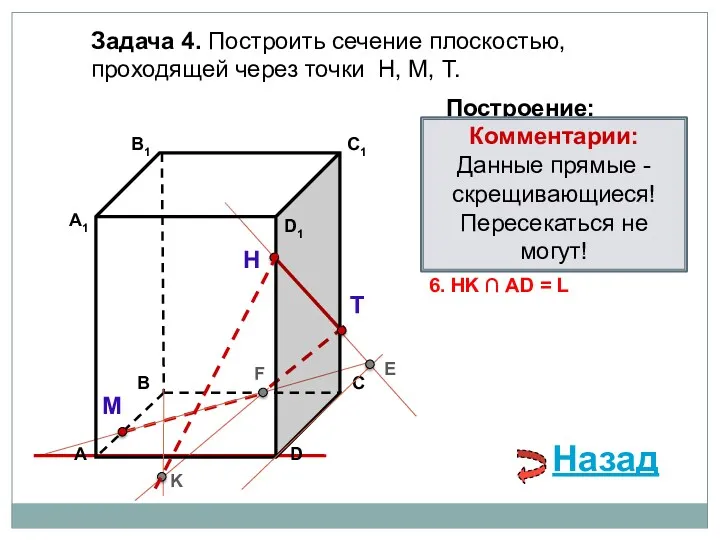
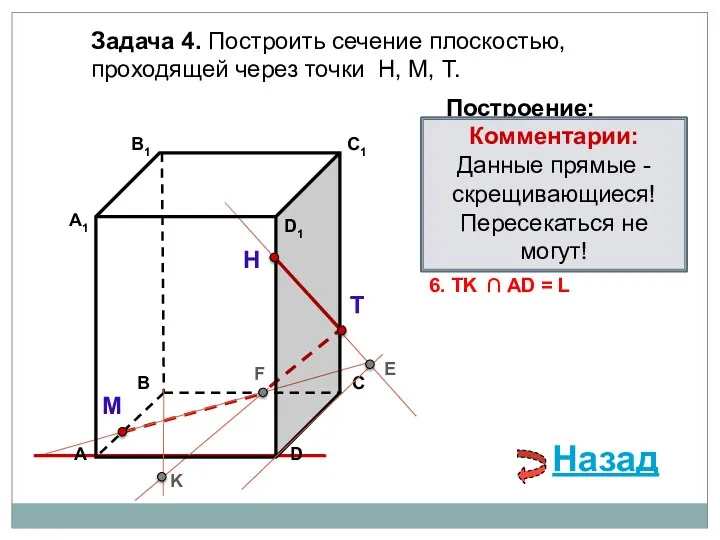
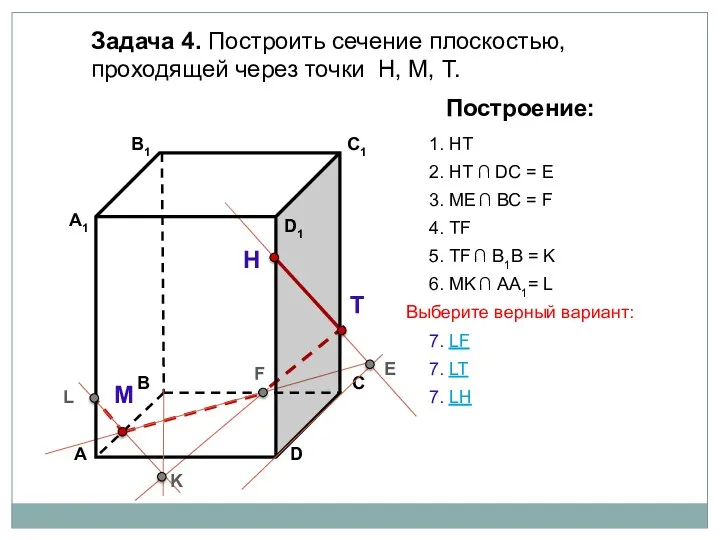
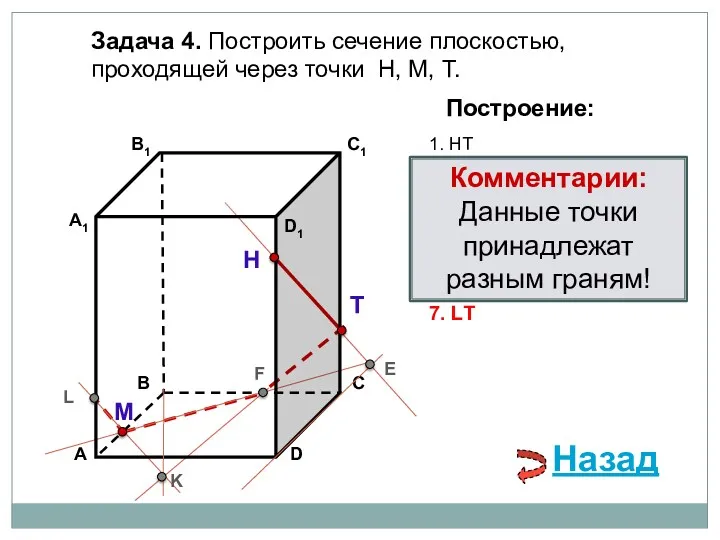
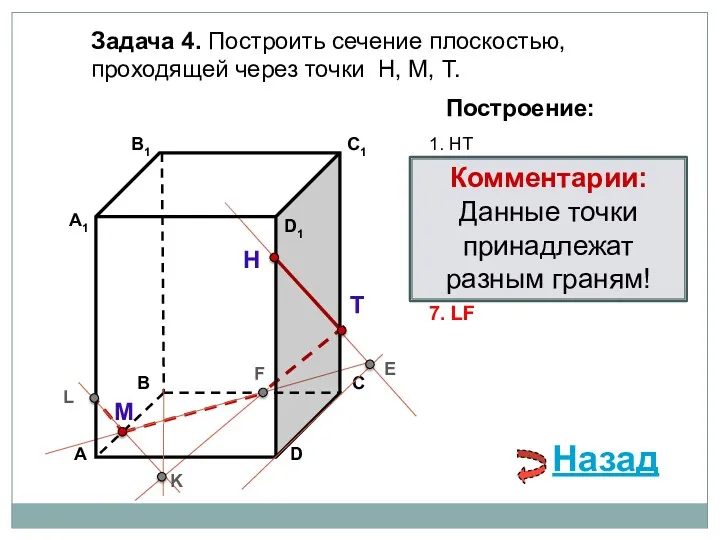
- 77. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 78. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
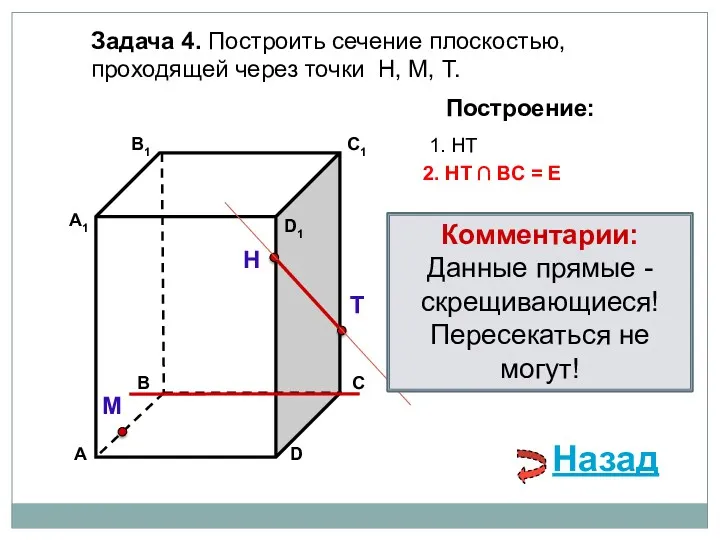
- 79. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
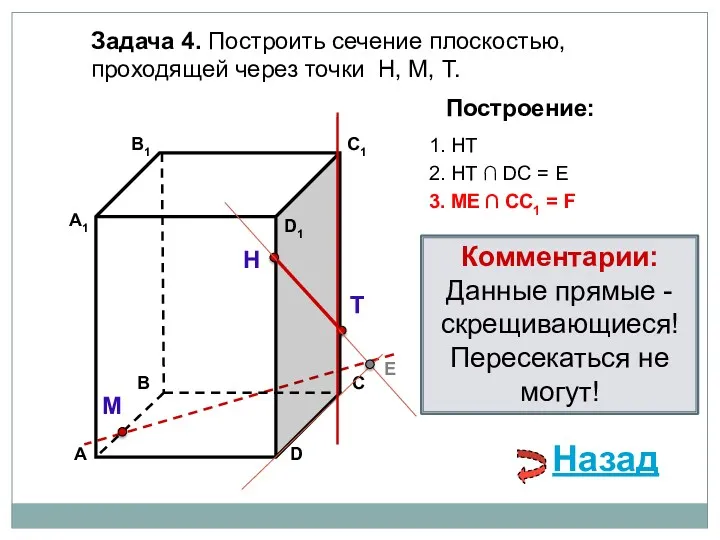
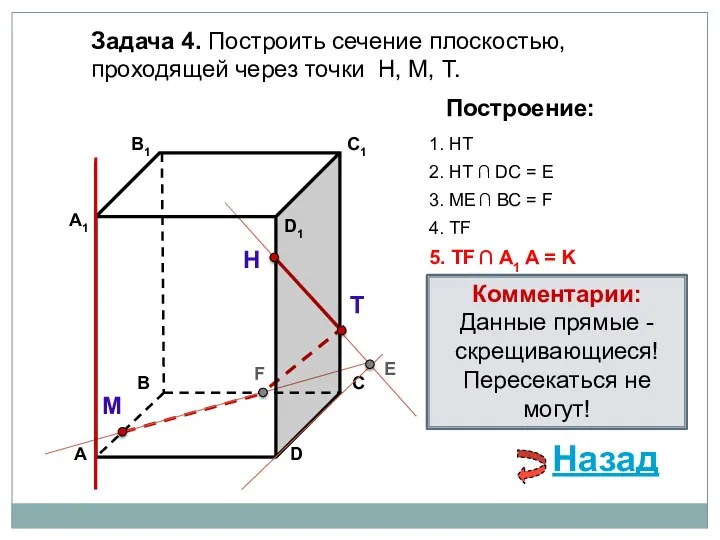
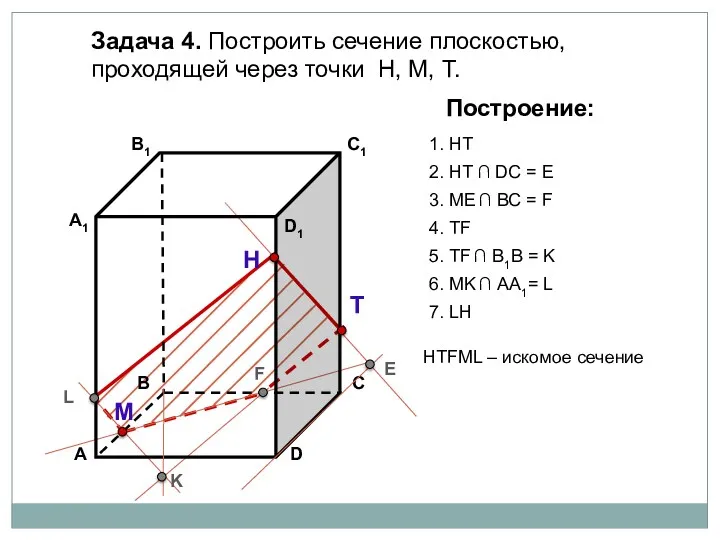
- 80. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 81. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
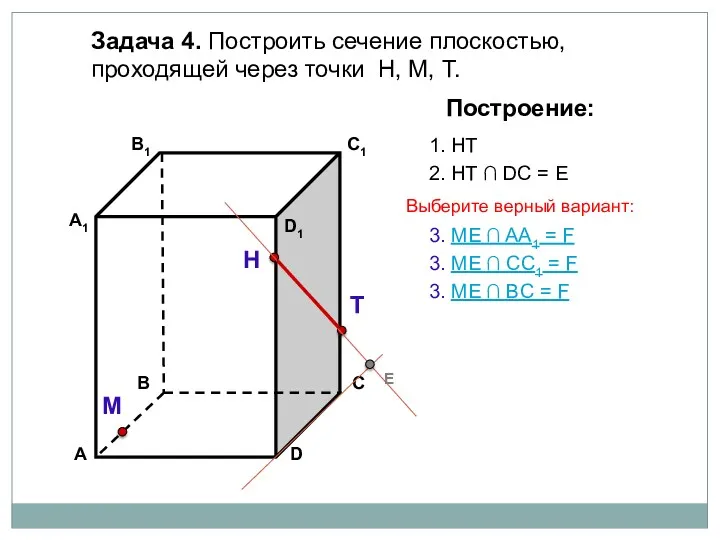
- 82. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
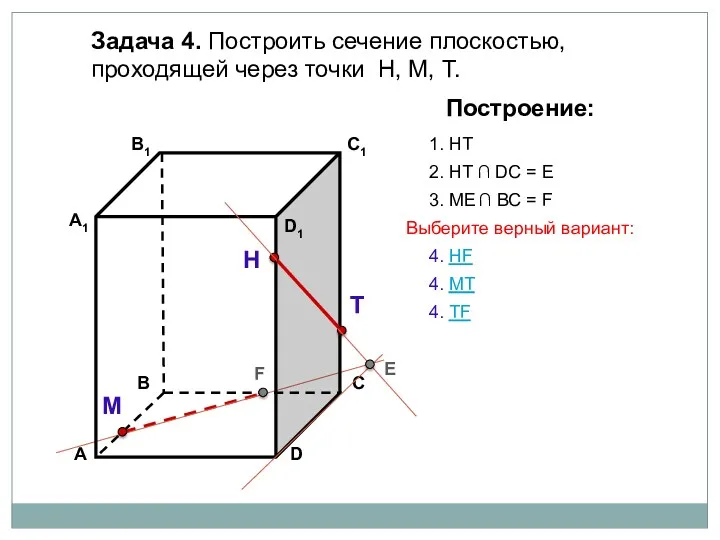
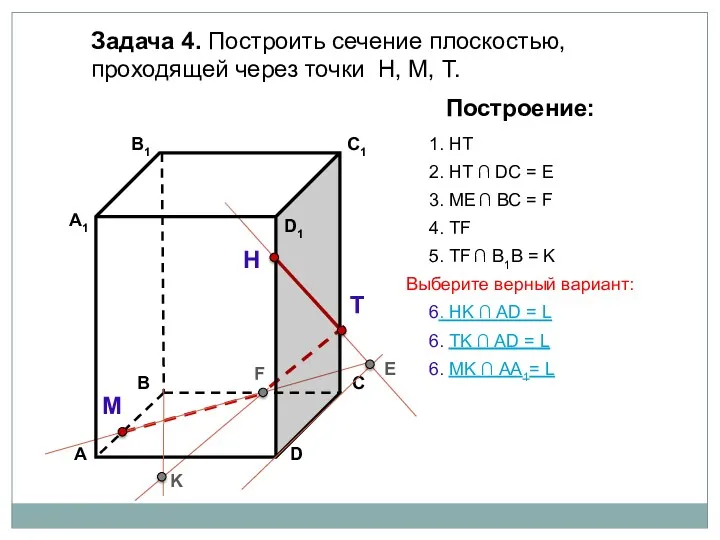
- 83. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 84. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 85. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
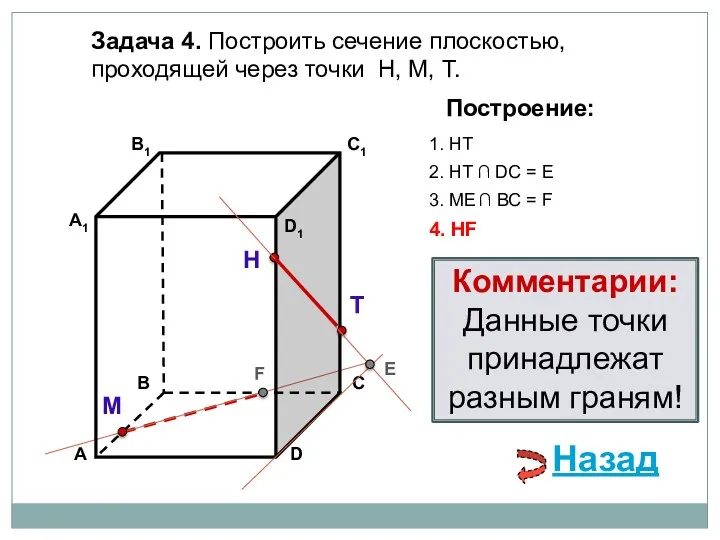
- 86. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 87. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 88. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 89. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 90. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 91. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 92. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 93. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
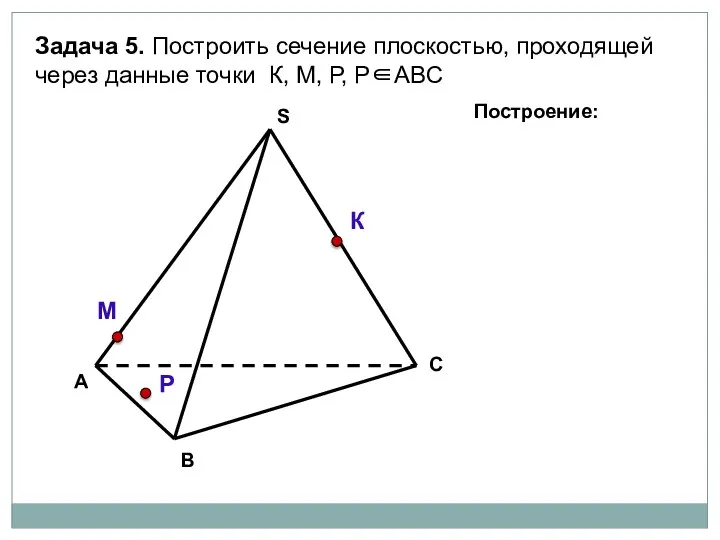
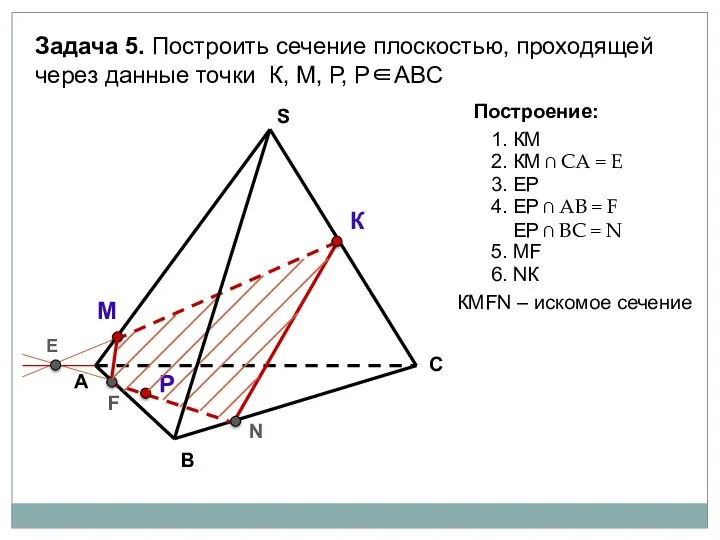
- 94. А В С S Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 95. А В С S Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 97. Скачать презентацию


















 Отношения и пропорции. Обобщающий урок в 6 классе
Отношения и пропорции. Обобщающий урок в 6 классе Решение треугольников. Теоремы синусов и косинусов
Решение треугольников. Теоремы синусов и косинусов Обратная функция
Обратная функция Сфера и шар. Вывод уравнения сферы
Сфера и шар. Вывод уравнения сферы Смешанные числа. Задачи
Смешанные числа. Задачи Дидактические игры на развитие элементарных математических представлений
Дидактические игры на развитие элементарных математических представлений Письменное деление многозначных чисел на однозначное число.
Письменное деление многозначных чисел на однозначное число. Занимательная математика.
Занимательная математика. Решение линейных уравнений с параметрами
Решение линейных уравнений с параметрами Свойства арифметического квадратного корня
Свойства арифметического квадратного корня Урок математики в 3 классе по теме: Единицы массы: грамм УМК Школа России.
Урок математики в 3 классе по теме: Единицы массы: грамм УМК Школа России. XIX ғасырдағы математиканың алпауыттары
XIX ғасырдағы математиканың алпауыттары Округление результатов расчета доверительного интервала
Округление результатов расчета доверительного интервала Числові множини. Ірраціональні та дійсні числа
Числові множини. Ірраціональні та дійсні числа Итоговый тест по математике. 5 класс
Итоговый тест по математике. 5 класс Тест по математике 4 класс Диск
Тест по математике 4 класс Диск Замечательные кривые
Замечательные кривые Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Сложение вида +2, +3
Сложение вида +2, +3 презентация найди цифру
презентация найди цифру Формула одновременного движения. Задачи на встречное движение.
Формула одновременного движения. Задачи на встречное движение. Кому нужна математика
Кому нужна математика Задачи для самостоятельной работы по начертательной геометрии
Задачи для самостоятельной работы по начертательной геометрии Презентация по математике Положение предметов на плоскости
Презентация по математике Положение предметов на плоскости Задачи на построение с помощью циркуля и линейки. 7 класс
Задачи на построение с помощью циркуля и линейки. 7 класс Решение задач на движение. Урок математики в 5 классе
Решение задач на движение. Урок математики в 5 классе Приемы умножения и деления на 10
Приемы умножения и деления на 10 Математическая викторина (8 класс)
Математическая викторина (8 класс)