Содержание
- 2. Содержание Теоретические факты: а) пропорциональные отрезки в треугольниках б) отношение площадей треугольников. Теорема Менелая. Применение теоремы
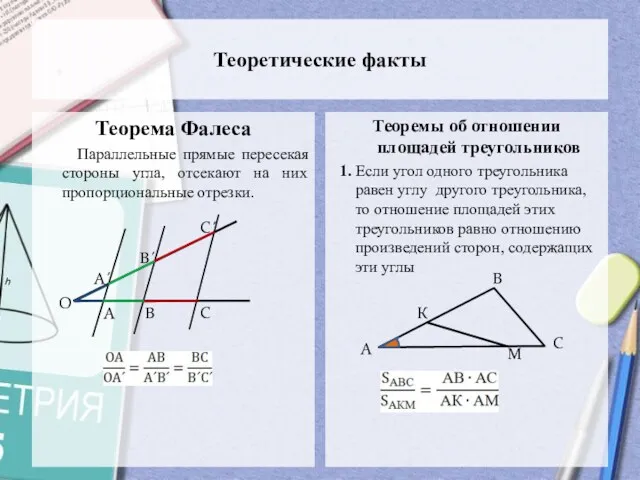
- 3. Теоретические факты Теорема Фалеса Параллельные прямые пересекая стороны угла, отсекают на них пропорциональные отрезки. Теоремы об
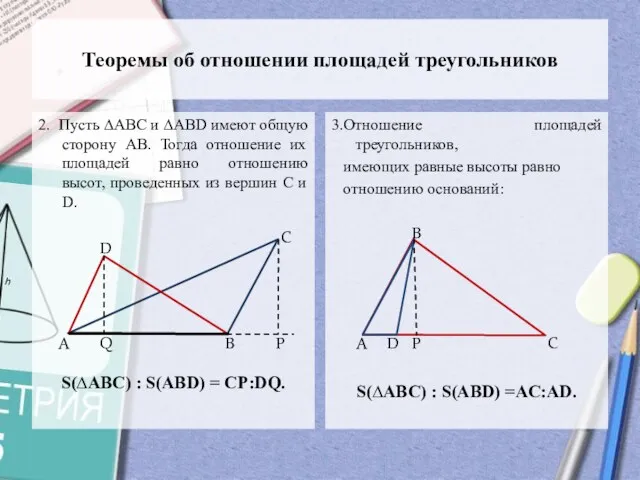
- 4. Теоремы об отношении площадей треугольников 2. Пусть ∆АВС и ∆АВD имеют общую сторону АВ. Тогда отношение
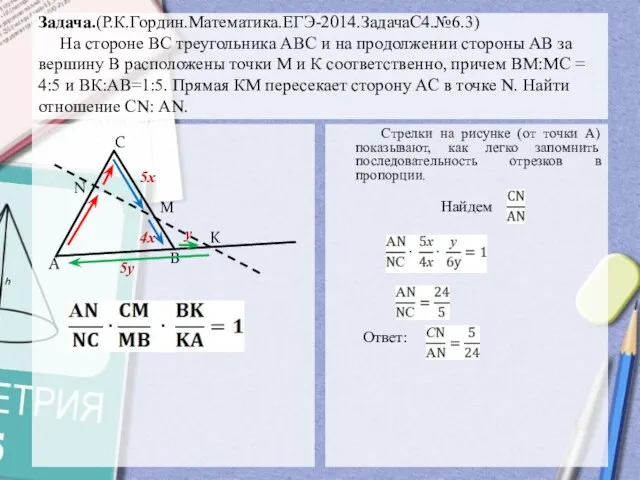
- 5. Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки
- 6. Предложенный вариант решения задачи – один из традиционных, без применения теоремы Менелая. Рассмотрим другой (более рациональный)
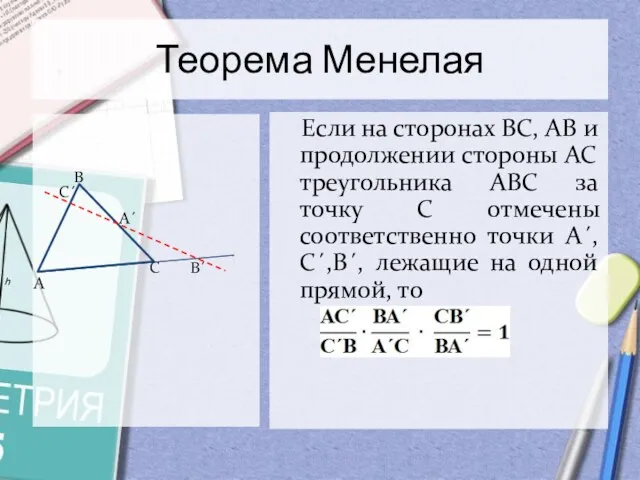
- 7. Теорема Менелая Если на сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С
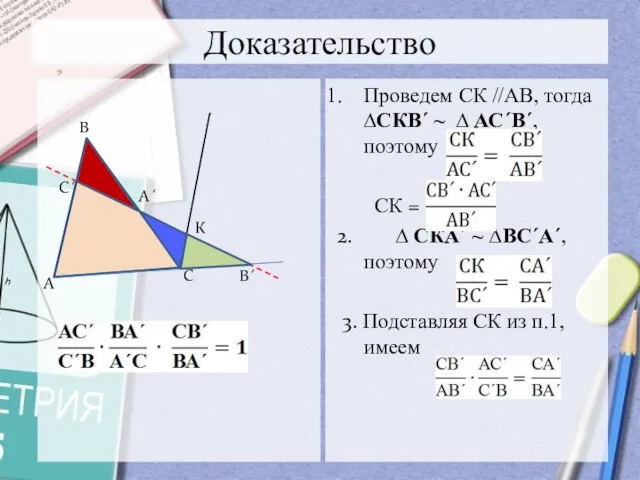
- 8. Доказательство Проведем СК //АВ, тогда ∆СКВ´ ~ ∆ АС´В´, поэтому СК = 2. ∆ СКА´ ~
- 9. Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки
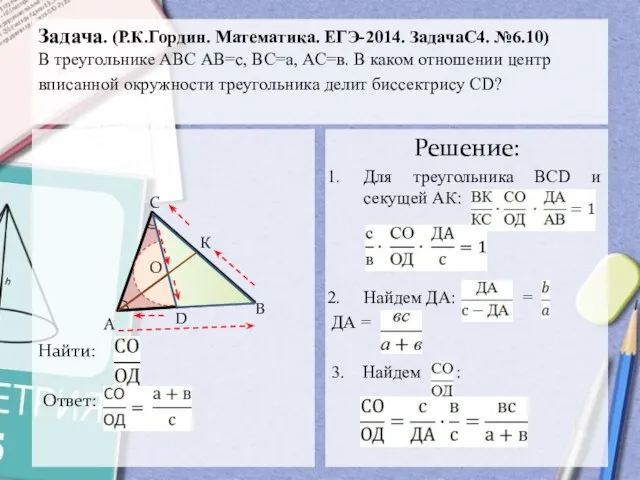
- 10. Найти: Ответ: Задача. (Р.К.Гордин. Математика. ЕГЭ-2014. ЗадачаС4. №6.10) В треугольнике АВС АВ=с, ВС=а, АС=в. В каком
- 11. Задача. (Р. К. Гордин. Математика. ЕГЭ-2014. Задача С4. №6.14) В ∆АВС, площадь которого равна 6, на
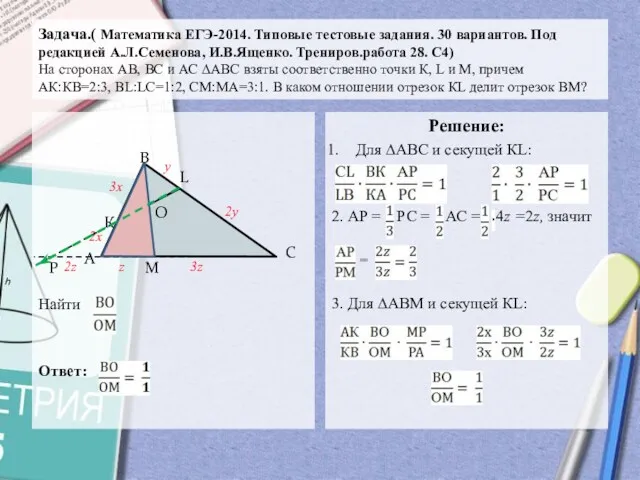
- 12. Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией А.Л.Семенова, И.В.Ященко. Трениров.работа 28. С4) На
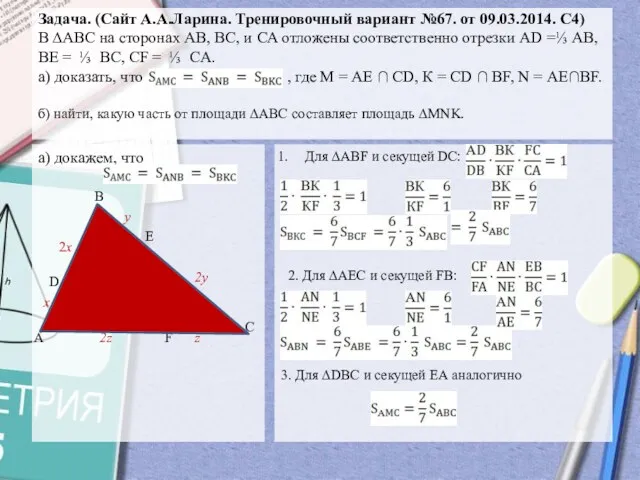
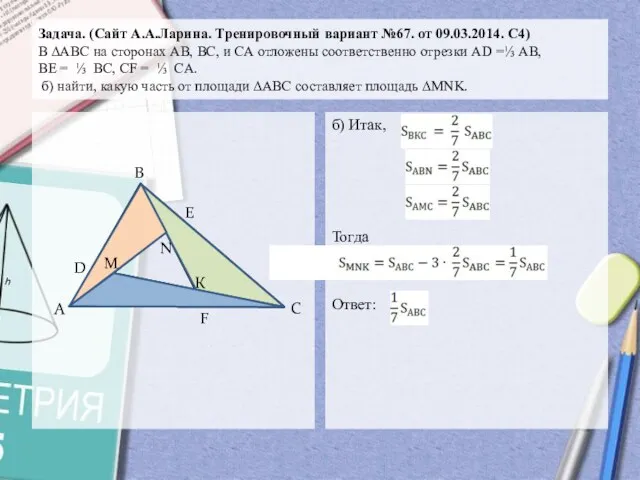
- 13. Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В ∆АВС на сторонах АВ, ВС, и
- 14. Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В ∆АВС на сторонах АВ, ВС, и
- 16. Скачать презентацию




 Математика. 1 класс. Урок 86. Числа от 10 до 20 - Презентация
Математика. 1 класс. Урок 86. Числа от 10 до 20 - Презентация Многочлены . Основные понятия
Многочлены . Основные понятия Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа
Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа Тест по теме: Пирамида. Часть 2. Вариант 2
Тест по теме: Пирамида. Часть 2. Вариант 2 Многоугольники
Многоугольники Уроки математики в 5 – 6 классах
Уроки математики в 5 – 6 классах Открытый урок математики во 2 классе МАТЕМАТИЧЕСКИЙ ЭЛЕКТРОННЫЙ ЖУРНАЛ
Открытый урок математики во 2 классе МАТЕМАТИЧЕСКИЙ ЭЛЕКТРОННЫЙ ЖУРНАЛ Разработка технологических карт и протоколов уроков по учебному предмету математика
Разработка технологических карт и протоколов уроков по учебному предмету математика Математическая викторина. Своя игра
Математическая викторина. Своя игра grafy1
grafy1 Презентация по математике 1 класс по теме Счет от 11 до 20
Презентация по математике 1 класс по теме Счет от 11 до 20 Пирамида в задачах ЕГЭ
Пирамида в задачах ЕГЭ Игра Счастливый случай. Внеклассное мероприятие по математике
Игра Счастливый случай. Внеклассное мероприятие по математике Математический час Это интересно знать!
Математический час Это интересно знать! Проект Математика вокруг нас 2 класс
Проект Математика вокруг нас 2 класс Главные направления линии второго порядка
Главные направления линии второго порядка презентация к уроку математики по теме Периметр 2 класс по программе Школа 2100
презентация к уроку математики по теме Периметр 2 класс по программе Школа 2100 Презентация Геометрические фигуры
Презентация Геометрические фигуры Итоговое повторение по курсу Алгебра и начала анализа 10 класс
Итоговое повторение по курсу Алгебра и начала анализа 10 класс Статистика и теория вероятностей. Испытания Бернулли. 9 класс
Статистика и теория вероятностей. Испытания Бернулли. 9 класс Числовые выражения, содержащие знаки + и -. Урок-путешествие За сокровищами
Числовые выражения, содержащие знаки + и -. Урок-путешествие За сокровищами Уменьшаемое. Вычитаемое. Разность
Уменьшаемое. Вычитаемое. Разность System of linear equations. Lecture 4-5
System of linear equations. Lecture 4-5 Математический тренажёр: Учим таблицу умножения для 2-3 классов.
Математический тренажёр: Учим таблицу умножения для 2-3 классов. Путешествие в страну Математики
Путешествие в страну Математики Задачи на построение треугольника
Задачи на построение треугольника Комплексные числа
Комплексные числа Презентация к уроку Зависимость величин(скорость, время, расстояние) Диск
Презентация к уроку Зависимость величин(скорость, время, расстояние) Диск