Содержание
- 2. 1. Динамическая система и ее математическая модель Динамическая система (ДС) - это любой объект или процесс,
- 3. Математическая модель ДС считается заданной, если введены параметры (координаты) системы, определяющие однозначно ее состояние, и указан
- 4. 2. Кинематическая интерпретация системы дифференциальных уравнений Рассмотрим ДС, моделируемые конечным числом обыкновенных дифференциальных уравнений. Для определения
- 5. Если рассматривать величины x1, x2, …, xN как координаты точки x в N-мерном пространстве, то получается
- 6. 3. Классификация динамических систем Система (1) может быть записана в векторной форме: (2) В этом случае
- 7. Если оператор предусматривает только линейные преобразования начального состояния, то он называется линейным. Линейный оператор обладает свойством
- 8. xn x0 n 0 1 2 x1 x2 x3 3 В общем виде систему с дискретным
- 9. Причины существования дискретных динамических систем. Многие процессы в природе имеют дискретный характер. Например, длительность светового дня
- 10. Г Фазовая траектория Г, характеризующая режим движения некоторой дифференциальной системы, последовательно и трансверсально пересекает поверхность S
- 11. От любой динамической системы с непрерывным временем можно перейти к соответствующему отображению, которое однозначно задается выбранным
- 12. 4. Итерирование линейного отображения. Если не сопоставлять количественно динамику отображения с поведением динамической системы с непрерывным
- 13. Проделаем процедуру итерирования на примере линейного отображения xn+1 = axn : m-кратное применение функции f( )
- 14. При a > 1 значение xn неограниченно увеличивается по закону геометрической прогрессии. Точное равенство a =
- 16. Скачать презентацию













 Объемы тел. 11 класс
Объемы тел. 11 класс Начала математического анализа
Начала математического анализа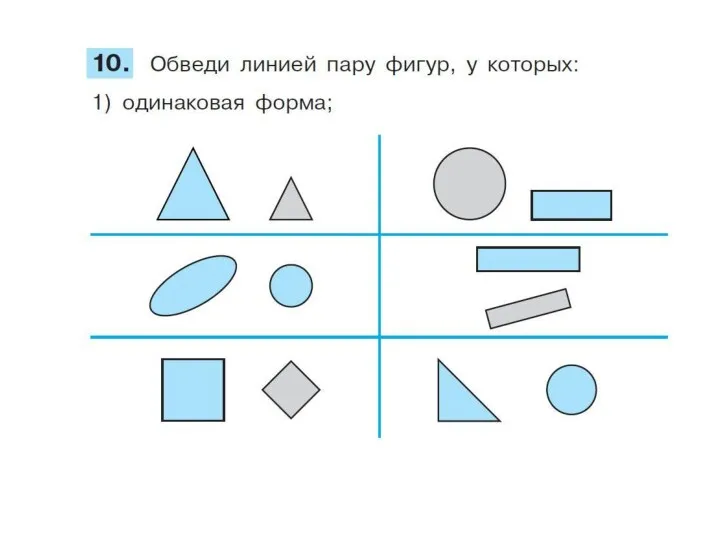 Презентация к уроку математики Признаки предметов. Построение таблиц или ряда предметов по определенному правилу.
Презентация к уроку математики Признаки предметов. Построение таблиц или ряда предметов по определенному правилу. Нахождение расстояния между двумя точками на координатной прямой
Нахождение расстояния между двумя точками на координатной прямой ЛИНЕЙНЫЕ И СТОЛБЧАТЫЕ ДИАГРАММЫ
ЛИНЕЙНЫЕ И СТОЛБЧАТЫЕ ДИАГРАММЫ Активизация познавательной деятельности обучающихся с нарушением интеллекта на уроках математики
Активизация познавательной деятельности обучающихся с нарушением интеллекта на уроках математики Единицы измерения длины в разное время и в разных странах
Единицы измерения длины в разное время и в разных странах Решение задач по теме Площадь параллелограмма, треугольника, трапеции
Решение задач по теме Площадь параллелограмма, треугольника, трапеции Анимашки для оформления презентаций в Microsoft Offis Power Point №4
Анимашки для оформления презентаций в Microsoft Offis Power Point №4 Подготовка к ЕГЭ по геометрии
Подготовка к ЕГЭ по геометрии Ведение в вейлет преобразование
Ведение в вейлет преобразование Вспоминаем, повторяем презентация к уроку закрепления изученного материала по математике в 1 классе
Вспоминаем, повторяем презентация к уроку закрепления изученного материала по математике в 1 классе Рациональные числа
Рациональные числа Блез Паскаль (1623-1662 гг.)
Блез Паскаль (1623-1662 гг.) Тригонометрические неравенства
Тригонометрические неравенства Презентация к занятию Путешествие в сказку Диск
Презентация к занятию Путешествие в сказку Диск Деление обыкновенных дробей. 6 класс
Деление обыкновенных дробей. 6 класс Перпендикуляр и наклонные. Расстояние от точки до плоскости
Перпендикуляр и наклонные. Расстояние от точки до плоскости Таблица умножения и деления на 6
Таблица умножения и деления на 6 Модуль действительного числа, уравнения
Модуль действительного числа, уравнения Табличные случаи умножения и деления
Табличные случаи умножения и деления Брей-ринг. Игра по математике
Брей-ринг. Игра по математике Перевірка ділення множенням. Розв’язування задачі, оберненої до задачі на знаходження суми двох добутків
Перевірка ділення множенням. Розв’язування задачі, оберненої до задачі на знаходження суми двох добутків Прямоугольник и квадрат
Прямоугольник и квадрат Четырехугольная призма
Четырехугольная призма Функция и ее свойства. Обобщающий урок. 9 класс
Функция и ее свойства. Обобщающий урок. 9 класс Презентация открытого урока по математике в третьем классе на темуПлощадь прямоугольников
Презентация открытого урока по математике в третьем классе на темуПлощадь прямоугольников Функция графигінің асимптоталары
Функция графигінің асимптоталары