Содержание
- 2. БИМАТРИЧНЫЕ ИГРЫ Предыдущие рассмотрения касались игр двух лиц, в которых интересы игроков были прямо противоположны. Однако
- 3. ПРИМЕРЫ БИМАТРИЧНЫХ ИГР Небольшая фирма А намерена сбывать товар на один из двух рынков, контролируемых другой
- 4. ПРИМЕР 2: ДИЛЕММА УЗНИКОВ Два узника А и В находятся в предварительном заключении по подозрению в
- 5. СМЕШАННАЯ СТРАТЕГИЯ Во всех приведенных примерах интересы игроков не совпадают. То надо построить такое комплексное решение,
- 6. Биматричные игры 2х2. Ситуация равновесия Рассмотрим ситуацию, когда у каждого две стратегии: Запишем средний выигрыш исходя
- 7. ОСНОВНОЕ ОПРЕДЕЛЕНИЕ: будем говорить. Что пара чисел (р*,q*), где р*,q* - вероятности от 0 до 1,
- 8. Запишем средние выигрыши игроков А и В в более удобной форме: НА(p,q) = (a11-a12-a21-+a22)pq + (a12
- 9. Вводятся следующие обозначения: С = a11- a12- a21+ a22 α = а22- а12 НА(p,q) - HA
- 10. Для игрока B Рассмотрим НB , пологая q = 0, потом q = 1 НB (p,0)
- 11. ВЫВОД Для того, чтобы в биматричной игре пара (р,q) определяла равновесную ситуацию, необходимо и достаточно выполнение
- 12. ПРИМЕР 1: БОРЬБА ЗА РЫНКИ С = a11-a12-a21+ a22 = -10 - 2 – 1 -
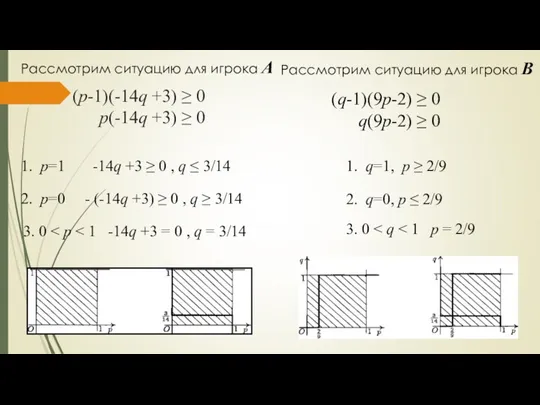
- 13. (р-1)(-14q +3) ≥ 0 p(-14q +3) ≥ 0 Рассмотрим ситуацию для игрока A 1. p=1 -14q
- 14. РЕШЕНИЕ НА(p,q) = (a11-a12-a21-a22)pq + (a12 – a22)p + (a21-a22)q + a22 НB(p,q) = (b11-b12-b21-b22)pq +
- 15. ПРИМЕР 2: ДИЛЕММА УЗНИКОВ С = a11-a12-a21+ a22 = 2, α = а22- а12 = 3
- 16. q 3/2 1 0 1 3/2 p Единственная равновесная ситуация — (0,0). Это ситуация, в которой
- 17. ЗАДАЧА 1. СЕМЕЙНЫЙ СПОР Два партнера договариваются о проведении одного из двух действий, (1) и (2)
- 18. С = a11-a12-a21+ a22 = 3, α = а22- а12 = 1 D = b11-b12-b21+ b22
- 19. ЗАДАЧА 2. СПОР АЛЬТРУИСТА И ЗГОИСТА Однажды решили поспорить альтруист и эгоист. Для этого они называют
- 21. Скачать презентацию

















 Теорема Пифагора
Теорема Пифагора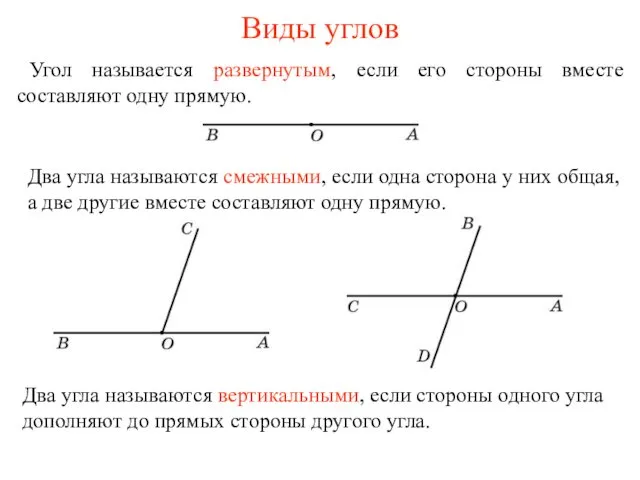 Виды углов
Виды углов Взаимно обратные числа. Урок № 1. 6 класс
Взаимно обратные числа. Урок № 1. 6 класс Використання формул скороченого множення для розкладання многочлена на множники
Використання формул скороченого множення для розкладання многочлена на множники Үлес
Үлес Задачи
Задачи Корреляционный анализ данных. Лекция 9
Корреляционный анализ данных. Лекция 9 Целые числа. Рациональные числа
Целые числа. Рациональные числа Задачи, 1 класс
Задачи, 1 класс Табличное сложение и вычитание
Табличное сложение и вычитание Случайные события. Вероятность наступления события
Случайные события. Вероятность наступления события Математика в истории
Математика в истории Цилиндр
Цилиндр Векторлар және векторларға амалдар қолдану
Векторлар және векторларға амалдар қолдану Формулы сокращенного умножения
Формулы сокращенного умножения Александрийский ученый Эратосфен. Решето Эратосфена
Александрийский ученый Эратосфен. Решето Эратосфена Тригонометрические выражения и их преобразования
Тригонометрические выражения и их преобразования Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32)
Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32) Определенный интеграл
Определенный интеграл Квадрат. Периметр квадрата
Квадрат. Периметр квадрата Равносильная замена при решении логарифмических неравенств. 11 класс
Равносильная замена при решении логарифмических неравенств. 11 класс Морской бой. Математика. 7 класс
Морской бой. Математика. 7 класс Теорема Пифагора - важнейшая теорема геометрии
Теорема Пифагора - важнейшая теорема геометрии Рациональные выражения. 8 класс
Рациональные выражения. 8 класс Расположение предметов по размеру.
Расположение предметов по размеру. Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы Число 7, цифра 7.
Число 7, цифра 7. Урок математики 2 класс Работа над ошибками
Урок математики 2 класс Работа над ошибками