Содержание
- 2. РАЗДЕЛ 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Глава 1. Одномерные СВ
- 3. УЧЕБНЫЕ ВОПРОСЫ Определения и классификация случайных величин. Ряд распределения. Функция распределения СВ, ее свойства и график.
- 4. ЛИТЕРАТУРА 1. Баврин И. И. Высшая математика. – М.: Академия, 2004, стр. 531 – 545. 2.
- 5. §1. Основные определения
- 6. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем заранее
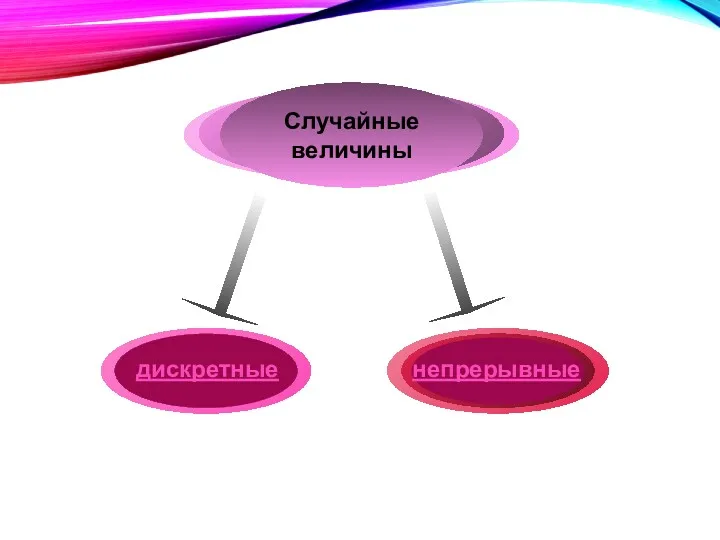
- 7. непрерывные дискретные
- 9. Определение. Непрерывной случайной величиной называют такую случайную величину, которая может принять любое значение из некоторого конечного
- 10. ПРИВЕДИТЕ ПРИМЕРЫ СЛУЧАЙНЫХ ВЕЛИЧИН
- 11. Закон распределения – всякое соответствие между возможными значениями случайной величины и соответствующими им вероятностями.
- 12. § 2. ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
- 13. ТАБЛИЧНЫЙ СПОСОБ
- 14. Пусть и и и ………………………………… ,
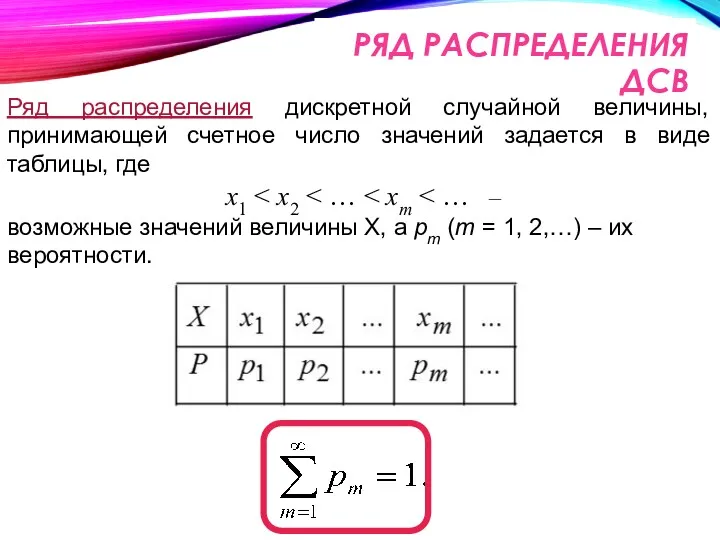
- 15. РЯД РАСПРЕДЕЛЕНИЯ ДСВ Закон распределения или ряд распределения дискретной случайной величины X, принимающей конечное число значений
- 16. Ряд распределения дискретной случайной величины, принимающей счетное число значений задается в виде таблицы, где x1 возможные
- 17. Два стрелка стреляют по цели по одному разу. Вероятность попадания: для первого стрелка 0,6; для второго
- 18. Ноль попаданий:
- 19. Одно попадание:
- 20. Два попадания:
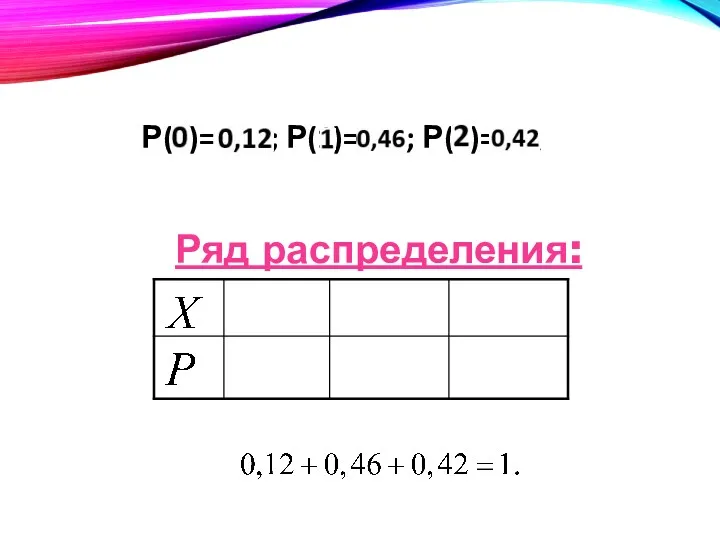
- 21. Ряд распределения: Р(0)= 0,1 ; Р(1)= 46 ; Р(2)=
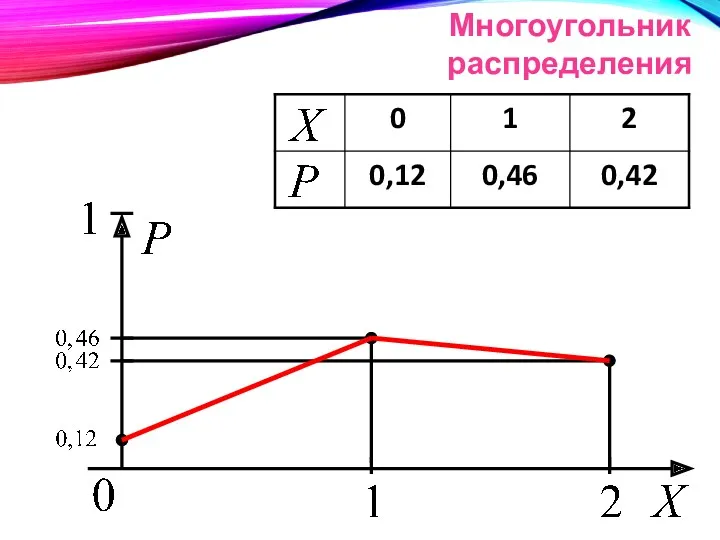
- 22. ГРАФИЧЕСКИЙ СПОСОБ
- 23. Многоугольник распределения
- 24. АНАЛИТИЧЕСКИЙ СПОСОБ
- 25. С ПОМОЩЬЮ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ F(X)
- 26. § 3. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 27. Определение. Функцией распределения случайной величины Х называется вероятность того, что случайная величина Х примет значение меньше,
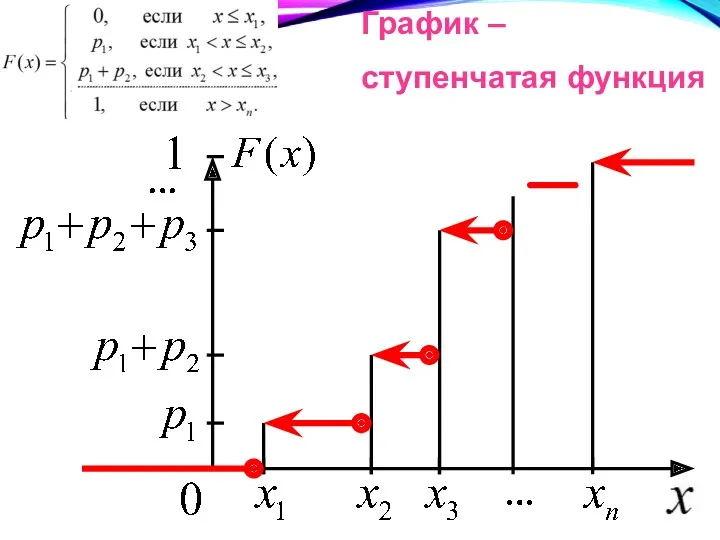
- 28. для ДСВ Х определяется формулой
- 29. График – ступенчатая функция
- 30. 1) 3) Свойства функции распределения
- 31. 4. Если - непрерывная случайная величина, то
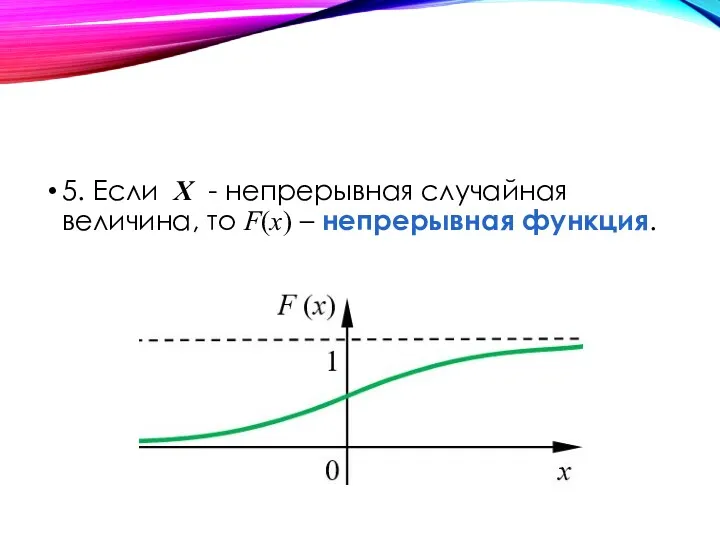
- 32. 5. Если Х - непрерывная случайная величина, то F(x) – непрерывная функция.
- 33. § 4. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
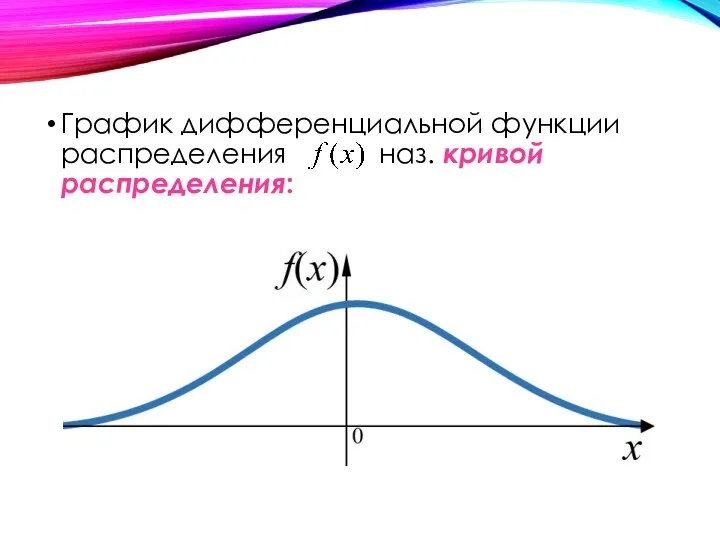
- 34. Определение. Дифференциальной функцией распределения или плотностью распределения вероятностей наз. первая производная интегральной функции распределения Иногда плотность
- 35. График дифференциальной функции распределения наз. кривой распределения:
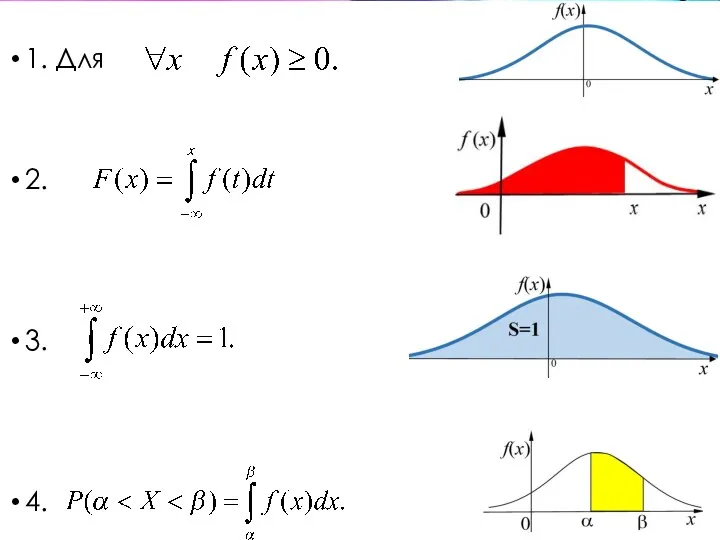
- 36. СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 37. 1. Для 2. 3. 4.
- 38. §5. Числовые характеристики СВ
- 39. Пусть Х - дискретная случайная величина с распределением вероятностей
- 40. Определение. Математическим ожиданием ДСВ Х называется число для конечного множества значений Х, для счетного множества значений
- 41. Рассмотрим случайную величину с рядом распределения: Пример.
- 42. Математическое ожидание случайной величины в нашем примере: М ( Х ) = x1· p1 + x2
- 43. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Определение. Математическим ожиданием непрерывной случайной величины Х, называется несобственный интеграл
- 44. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ В случае, когда все возможные значения НСВ Х принадлежат отрезку [a,b],
- 45. Свойства математического ожидания 1. Если X ≡ С = const, то МC = С. 2. Если
- 46. ДИСПЕРСИЯ
- 48. Вычисление дисперсии Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее
- 49. Вычисление дисперсии
- 50. Дисперсия непрерывной случайной величины вычисляется по формуле ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СВ
- 51. Для практического вычисления дисперсии используется формула ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СВ
- 52. СВОЙСТВА ДИСПЕРСИИ 10. D [ a ] = 0, a = const; 20. D [ a
- 53. СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ Определение. Средним квадратическим отклонением (СКО) случайной величины называется корень квадратный из ее дисперсии.
- 54. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН Пример. Случайным образом бросают точку на отрезок [ 0,1 ]. Х– координата
- 55. Определение. Модой М0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода
- 56. Определение. Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или
- 57. Определение. Начальным моментом αk k-го порядка СВ Х называется Определение. Центральным моментом μk k-го порядка СВ
- 58. НАЧАЛЬНЫЕ МОМЕНТЫ
- 59. ЦЕНТРАЛЬНЫЕ МОМЕНТЫ
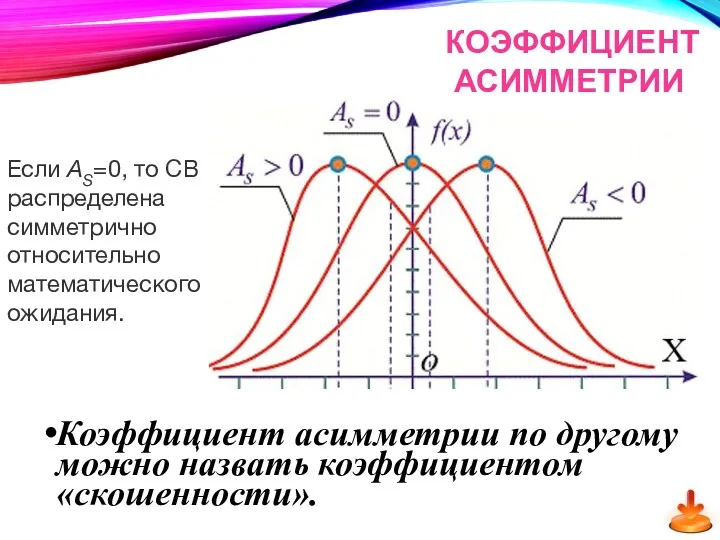
- 60. Определение. Коэффициентом асимметрии AS называется величина КОЭФФИЦИЕНТ АСИММЕТРИИ
- 61. Коэффициент асимметрии по другому можно назвать коэффициентом «скошенности». Определение. Для характеристики островершинности и плосковершинности распределения используется
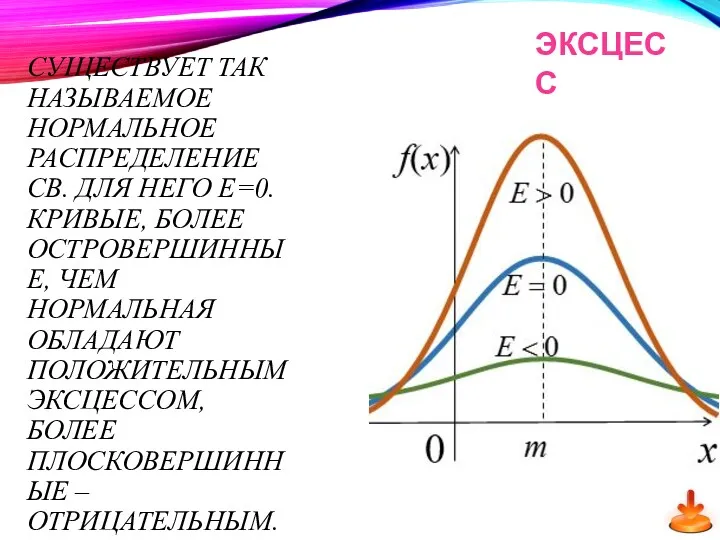
- 62. Определение. Эксцессом Е называется величина ЭКСЦЕСС
- 63. СУЩЕСТВУЕТ ТАК НАЗЫВАЕМОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СВ. ДЛЯ НЕГО Е=0. КРИВЫЕ, БОЛЕЕ ОСТРОВЕРШИННЫЕ, ЧЕМ НОРМАЛЬНАЯ ОБЛАДАЮТ ПОЛОЖИТЕЛЬНЫМ
- 65. Скачать презентацию











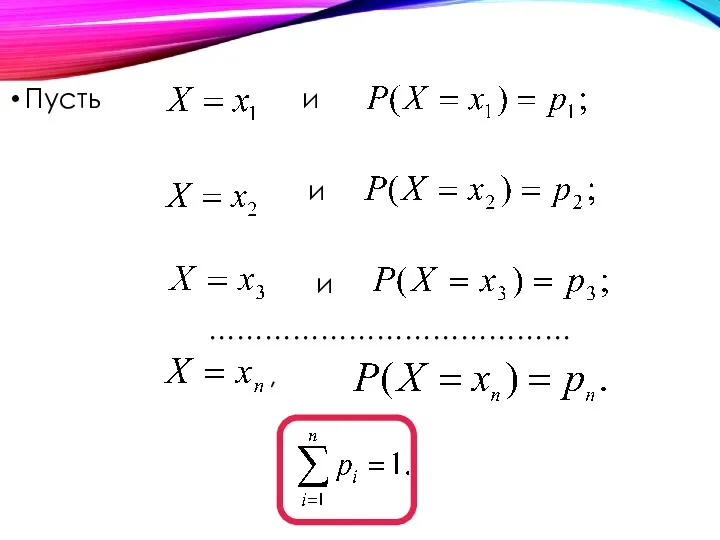












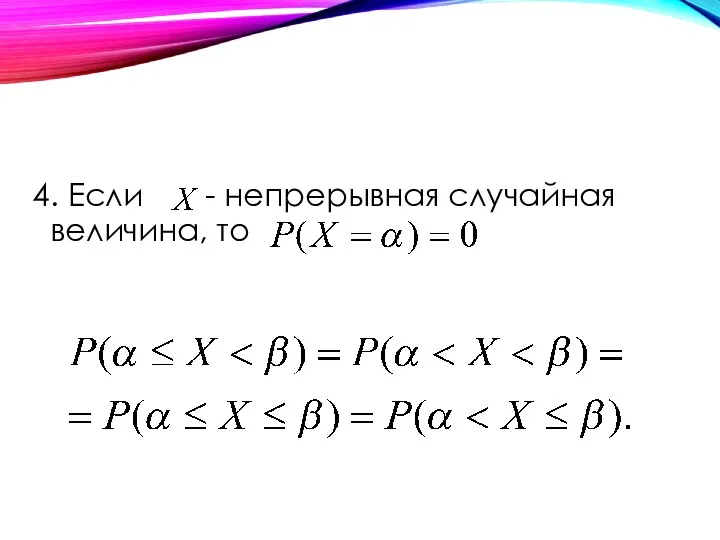
















![СВОЙСТВА ДИСПЕРСИИ 10. D [ a ] = 0, a](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/19084/slide-51.jpg)









 Решение задач по теме Площади фигур
Решение задач по теме Площади фигур Презентация по математике.
Презентация по математике. Дифференциальное исчисление
Дифференциальное исчисление Углы. Измерение углов. Построение углов. 5 класс
Углы. Измерение углов. Построение углов. 5 класс Математика.Тема урока: Числа от 1 до 10.
Математика.Тема урока: Числа от 1 до 10. Замена произведения чисел их суммой
Замена произведения чисел их суммой Неопределенный интеграл
Неопределенный интеграл Задачи на переливание жидкости
Задачи на переливание жидкости Теория графов: основные понятия и определения
Теория графов: основные понятия и определения Угол. Прямой угол (с применением ИКТ)
Угол. Прямой угол (с применением ИКТ) презентации по математике
презентации по математике Теорема о биссектрисе треугольника
Теорема о биссектрисе треугольника Среднее арифметическое, размах и мода ряда чисел
Среднее арифметическое, размах и мода ряда чисел Вивчаємо арифметичні дії множення і ділення; табличне множення та ділення
Вивчаємо арифметичні дії множення і ділення; табличне множення та ділення Конспект урока математики во 2 классе. Умножение
Конспект урока математики во 2 классе. Умножение Функции и ее графики
Функции и ее графики Путешествие по математическим станциям
Путешествие по математическим станциям КУС по математике для 4 класса
КУС по математике для 4 класса Ученые математики
Ученые математики Понятие бесконечной интегральной суммы. Интеграл (11 класс)
Понятие бесконечной интегральной суммы. Интеграл (11 класс) Перпендикулярність прямої і площини
Перпендикулярність прямої і площини Основные формулы комбинаторики. Классическое определение вероятности. Теоремы сложения и умножения вероятностей
Основные формулы комбинаторики. Классическое определение вероятности. Теоремы сложения и умножения вероятностей Понятие площади многоугольника
Понятие площади многоугольника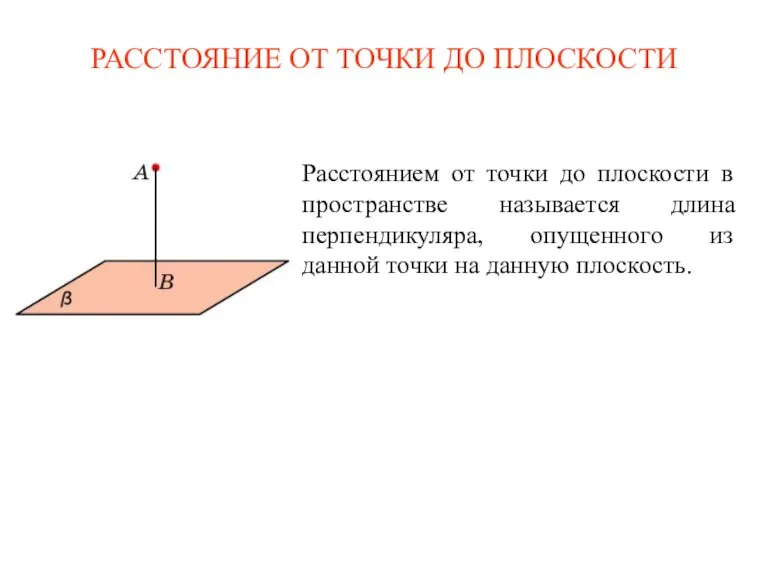 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Топқа бөлу
Топқа бөлу Педагогический опыт Развитие логического мышления и математических представлений у детей дошкольного возраста через развивающие игры
Педагогический опыт Развитие логического мышления и математических представлений у детей дошкольного возраста через развивающие игры Задачи на сравнение
Задачи на сравнение Упрощение выражений, 5 класс
Упрощение выражений, 5 класс