Содержание
- 2. Теория вероятностей – математическая наука, изучающая закономерности случайных явлений, случайные события, случайные величины, их свойства и
- 3. Задачи называются комбинаторными, если в них определяется число способов осуществления того или иного действия ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
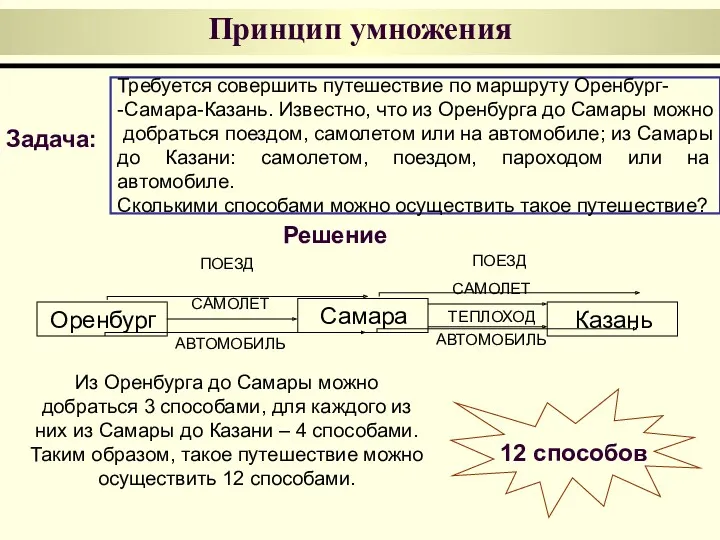
- 4. Принцип умножения Требуется совершить путешествие по маршруту Оренбург- -Самара-Казань. Известно, что из Оренбурга до Самары можно
- 5. Принцип умножения Если требуется выполнить одно за другим k действий, причем первое действие можно выполнить способами,
- 6. Различные упорядоченные множества одного и того же множества из n элементов называются перестановками этого множества ПЕРЕСТАНОВКИ
- 7. ПЕРЕСТАНОВКИ Теорема Число перестановок множества из n элементов равно Доказательство: Определим сколькими способами n предметов можно
- 8. Упорядоченное m-элементное подмножество множества из n элементов называется размещением из n элементов по m РАЗМЕЩЕНИЯ Как
- 9. РАЗМЕЩЕНИЯ Теорема Число размещений множества из n элементов по m равно Доказательство: 1-ый элемент можно выбрать
- 10. Произвольное m-элементное подмножество множества из n элементов называется сочетанием из n элементов по m СОЧЕТАНИЯ Как
- 11. СОЧЕТАНИЯ Теорема Число сочетаний множества из n элементов по m равно Доказательство: Известно, что число упорядоченных
- 12. Представление (разложение) множества из n элементов в виде суммы (объединения) r попарно непересекающихся неупорядоченных подмножеств, состоящих
- 13. 1-ое множество, состоящее из m1 элементов, можно выбрать способами; 2-ое множество - способами; ….. (r-1)-ое множество
- 14. Случайным событием (просто событием, исходом) называется любой факт, который в результате испытания может произойти или не
- 15. Элементарные исходы – это события, обладающие следующими cвойствами; они взаимно исключают друг друга и в результате
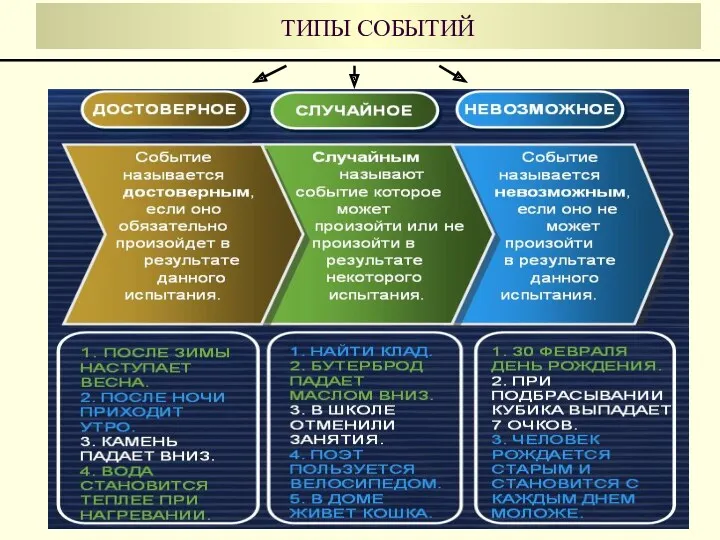
- 16. ТИПЫ СОБЫТИЙ
- 17. Элементарными событиями являются: - выпадение цифры «0»; - выпадение цифры «1»; - выпадение цифры «2»; -
- 18. ПРИМЕР Предположим, в результате опыта появилась цифра 7. В этом случае произошли события B и C,
- 19. Суммой событий А и B называется событие ОПЕРАЦИИ НАД СОБЫТИЯМИ Определение ОБОЗНАЧЕНИЕ С=А+B или Событие А+В
- 20. Произведением событий А и B называется событие ОПЕРАЦИИ НАД СОБЫТИЯМИ Определение ОБОЗНАЧЕНИЕ С=АB или Событие АВ
- 21. Разностью событий А и B называется событие ОПЕРАЦИИ НАД СОБЫТИЯМИ Определение ОБОЗНАЧЕНИЕ С=А-B или Событие А-В
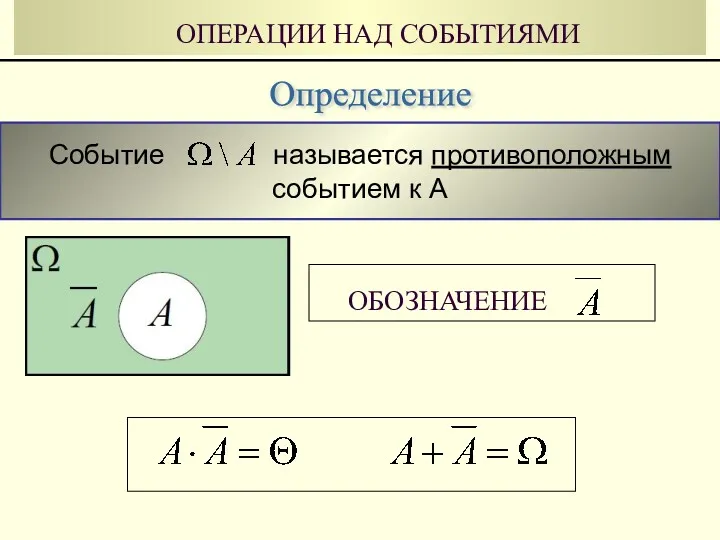
- 22. Событие называется противоположным событием к А ОПЕРАЦИИ НАД СОБЫТИЯМИ Определение ОБОЗНАЧЕНИЕ
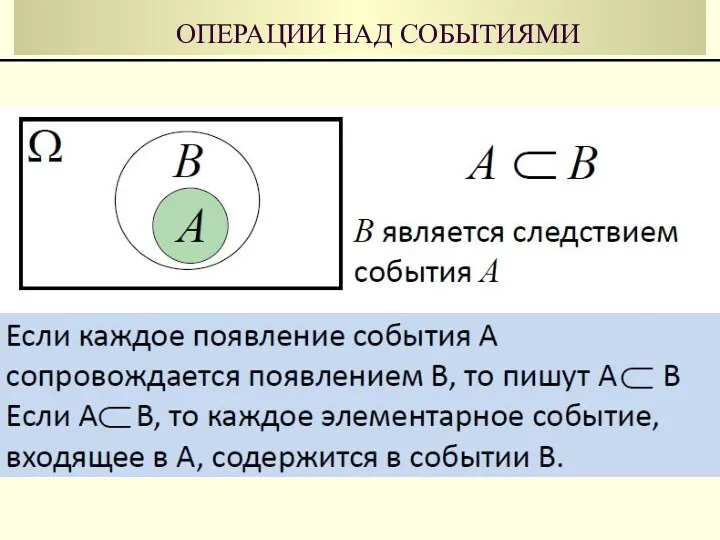
- 23. ОПЕРАЦИИ НАД СОБЫТИЯМИ
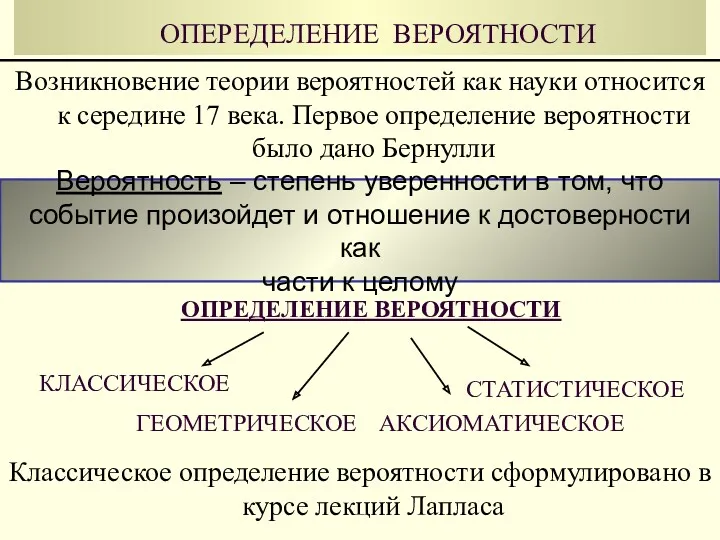
- 24. ОПЕРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Возникновение теории вероятностей как науки относится к середине 17 века. Первое определение вероятности было
- 25. Вероятностью события А называется число, равное отношению числа элементарных исходов, благоприятствующих появлению события А к общему
- 26. Невозможному событию не соответствует ни одного исхода СВОЙСТВА КЛАССИЧЕСКОГО ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ Каждому элементарному событию соответствует только
- 27. СВОЙСТВА КЛАССИЧЕСКОГО ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ЗАМЕЧАНИЕ Классическое определение вероятности может применяться лишь в тех случаях, когда: пространство
- 28. Элементарными событиями являются: - выпадение цифры «0»; - выпадение цифры «1»; - выпадение цифры «2»; -
- 29. - событие, состоящее в том, что выпадет четная цифра; - событие, состоящее в том, что выпадет
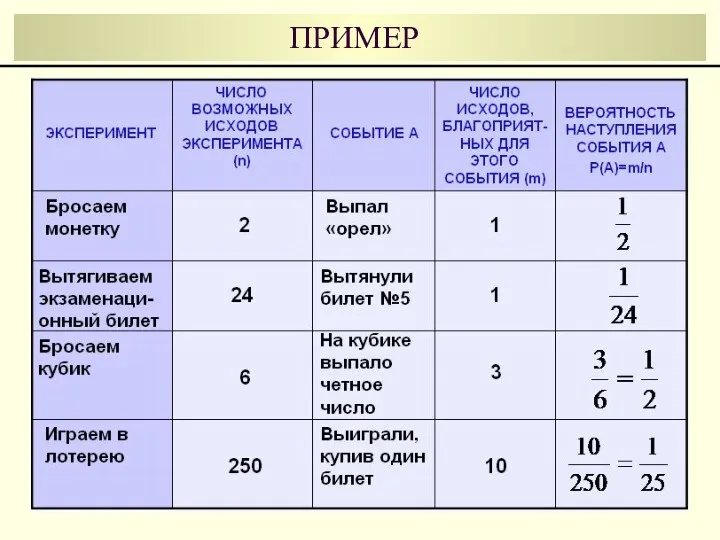
- 30. ПРИМЕР
- 31. ОПЕРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Геометрическая интерпретация вероятности была предложена английским математиком Венном Геометрическое определение вероятности применяется в тех
- 32. Вероятностью события А, состоящего в том, что при бросании точки на отрезок [A, B] она попадет
- 33. Вероятностью события А, состоящего в том, что при бросании точки в область G она попадет в
- 34. Вероятностью события А, состоящего в том, что при бросании точки в область T она попадет в
- 35. Мера области, соответствующая элементарному событию, равна нулю . Благоприятной области для невозможного события нет СВОЙСТВА ГЕОМЕТРИЧЕСКОГО
- 36. Пусть время прихода одного из них – 12 ч. х мин.; другого – 12 ч. y
- 37. ОПЕРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Определение (статистическое определение вероятности) Статистическое определение вероятности является следствием обработки результатов различных наблюдений и
- 38. СВОЙСТВА ЧАСТОТЫ Например, если бросили монету 3 раза и каждый раз выпало «решка», то частота появления
- 39. ОПЕРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Опыты показывают, что при больших N частота νА в различных сериях испытаний оказывается приближенно
- 40. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии
- 41. Так как известно, что синие шары не вынимались, то всего существует n=20 возможных вариантов исхода опыта.
- 42. События A1, А2,…,Аn называются попарно независимыми, если . События A и B называются независимыми, если Так
- 43. Совокупность событий {А1, А2,…,Аn} называется полной группой событий, если: события А1, А2,…, Аn попарно независимы, то
- 44. Пусть известны вероятности событий и условные вероятности . Как найти вероятность события A? Если события A1,
- 45. Опыт произведен. В результате наступило событие А. Как изменятся вероятности гипотез ? То есть как найти
- 46. Обозначим B1 и B2 попадания соответственно при 1-ом и 2-ом выстреле. Введем гипотезы А2– два попадания
- 47. Пусть производится n независимых испытаний, в каждом из которых событие А может появиться или нет, причем
- 48. Вероятность того, что событие А наступит хотя бы один раз при проведении испытаний по схеме Бернулли
- 49. ПРИМЕР Чему равна вероятность того, что при четырех подбрасываниях игральной кости тройка выпадет 2 раза? Задача:
- 50. НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО НАСТУПЛЕНИЯ СОБЫТИЯ ПРИ ПРОВЕДЕНИИ ИСПЫТАНИЙ ПО СХЕМЕ БЕРНУЛЛИ Рабочий обслуживает 12 одноименных станков. Вероятность
- 51. Если np-q – целое число, то так как np+p=np+1-q=np-q+1 – целое число, то значений будет два
- 52. ПРИМЕР В ВУЗе обучаются 730 студентов. Вероятность того, что день рождение наугад взятого студента приходится на
- 53. Если количество n испытаний Бернулли велико, а . (то есть вероятность появления события А в каждом
- 54. ПРИМЕР
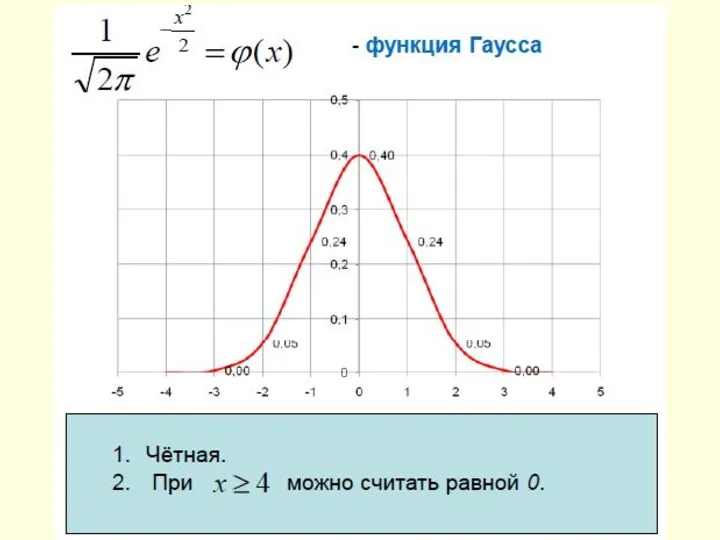
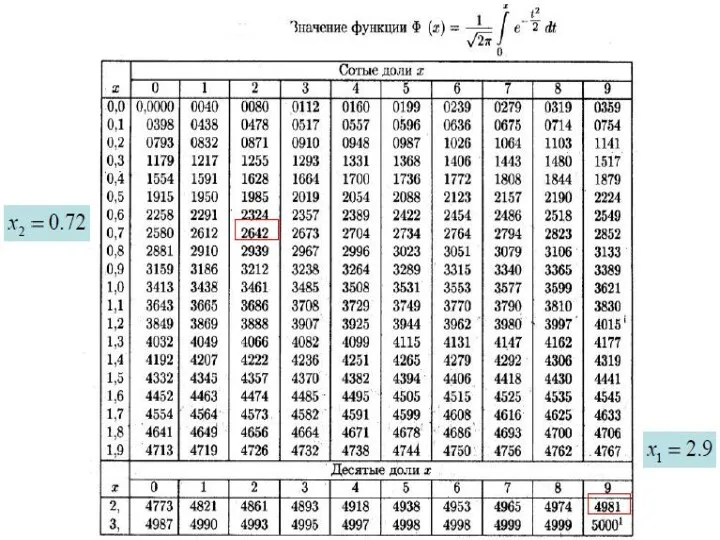
- 55. Вероятность того, что в n (n>>1) независимых испытаниях Бернулли событие А произойдет ровно m раз, может
- 57. ПРИМЕР
- 59. Вероятность того, что в n (n>>1) независимых испытаниях событие А произойдет от m1 до m2 раз,
- 60. ПРИМЕР
- 63. Скачать презентацию




















































 Способы решения систем линейных уравнений: метод подстановки
Способы решения систем линейных уравнений: метод подстановки Число 9, цифра 9
Число 9, цифра 9 Умные задачки
Умные задачки Система использования ключевых задач геометрии при обучении математике
Система использования ключевых задач геометрии при обучении математике Округление натуральных чисел
Округление натуральных чисел Конус в природі
Конус в природі Единицы измерения длины
Единицы измерения длины Десятичные дроби. Математика и экология (часть 1)
Десятичные дроби. Математика и экология (часть 1) Решение заданий В10 по материалам открытого банка задач ЕГЭ
Решение заданий В10 по материалам открытого банка задач ЕГЭ Программа курса по высшей математике
Программа курса по высшей математике Параллелепипед. Геометрия. 10 класс
Параллелепипед. Геометрия. 10 класс Значение чисел в нашей жизни
Значение чисел в нашей жизни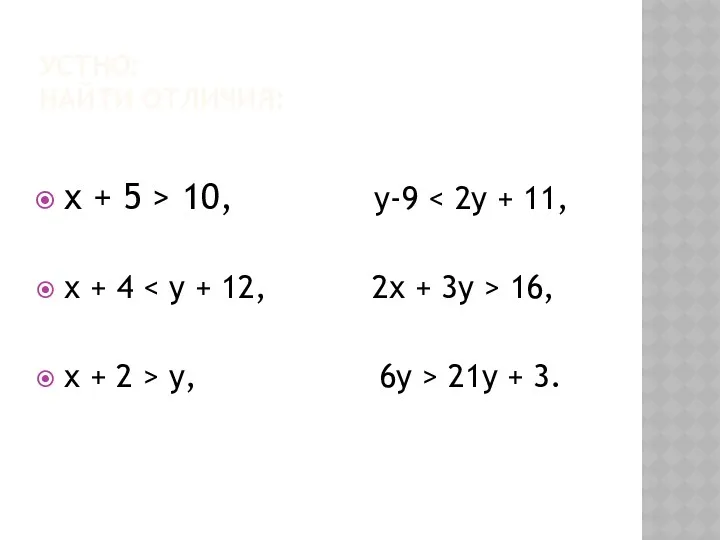 Решение неравенств с двумя переменными
Решение неравенств с двумя переменными Теория графов
Теория графов Алгебраические уравнения. Задания для устного счета
Алгебраические уравнения. Задания для устного счета Округление натуральных чисел. Повторение изученного
Округление натуральных чисел. Повторение изученного Учимся выполнять умножение. урок 37. 1 класс. УМК Начальная школа 21 века
Учимся выполнять умножение. урок 37. 1 класс. УМК Начальная школа 21 века Экономические задачи
Экономические задачи Имитационное моделирование. Методология моделирования систем
Имитационное моделирование. Методология моделирования систем Цилиндр, конус и шар
Цилиндр, конус и шар периметр
периметр Работа по учебнику Г.К. Муравина, О.В. Муравиной Математика 5 для общеобразовательных учреждений
Работа по учебнику Г.К. Муравина, О.В. Муравиной Математика 5 для общеобразовательных учреждений Закрепление изученного в 4 классе
Закрепление изученного в 4 классе Работа с графиками. ЕГЭ по математике, задания В9
Работа с графиками. ЕГЭ по математике, задания В9 Методы теории игр
Методы теории игр Функция и ее свойства
Функция и ее свойства Числовые выражения. 7 класс
Числовые выражения. 7 класс Презентация по математике по теме Задача для 1 класса
Презентация по математике по теме Задача для 1 класса