Слайд 2

Точка
Точка в пространстве и на чертеже может быть задана:
Координатами в
прямоугольной системе координат.
Двумя пересекающимися прямыми.
Вершинами гранной фигуры.
Ортогональный чертеж (эпюр) точки представляет собой совокупность двух ее ортогональных проекций, соединенных линией связи, перпендикулярной координатной оси.
Абсцисса (X) точки А – это отрезок, измеряемый в мм и откладываемый на эпюре по координатной оси 0х влево от начала координат 0.
Ордината (Y) точки А – это отрезок, измеряемый и откладываемый на эпюре по линии связи от координатной оси 0х вниз при положительном значении ординаты и вверх – при отрицательном.
Аппликата (Z) точки А – это отрезок, измеряемый и откладываемый на эпюре по линии связи от координатной оси 0х вверх при положительном значении аппликаты и вниз – при отрицательном.
Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Прямая
Прямая в пространстве и на чертеже может быть задана:
Двумя точками.
Точкой и
направлением.
Двумя пересекающимися плоскостями.
Рассматриваются:
а) прямые общего положения (они не параллельны ни одной из трех плоскостей проекций);
б) прямые частного положения:
уровня, т.е. параллельные одной из трех плоскостей проекций, на указанные плоскости они проецируются в натуральную величину (НВ):
- горизонтальные – параллельные П1 ;
- фронтальные – параллельные П2;
- профильные – параллельные П3 .
проецирующие, т.е. перпендикулярные одной трех плоскостей
проекций: ⊥П1 ;⊥П2 ; ⊥П3 . Эти прямые проецируются на
указанные плоскости вырождено – в виде точки.
Слайд 9
Слайд 10

Слайд 11

Слайд 12
Слайд 13

Слайд 14

Слайд 15

Слайд 16

Плоскость
Плоскость в пространстве и на чертеже может быть задана:
1. Тремя
точками, не лежащими на одной прямой: α(АВС).
2. Прямой и точкой, не лежащей на этой прямой: β (l, A).
3. Двумя пересекающимися прямыми: δ (m ∩ n).
4. Двумя параллельными прямыми: γ(b II c).
5. Плоской кривой σ(∪ m).
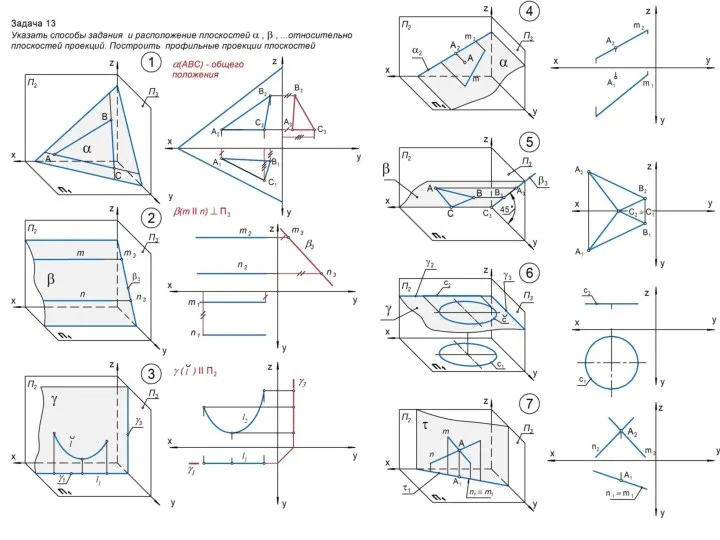
Рассматривают:
Плоскости общего положения, неперпендикулярные ни одной из трех плоскостей проекций;
Плоскости частного положения:
- проецирующие ( ⊥ П1 ; ⊥ П2 ; ⊥ П3 ), имеющие на
указанных плоскостях вырожденные проекции в виде
прямых линий;
- уровня ( II П1 ; II П2 ; II П3 ), являющиеся дважды
проецирующими.
Слайд 17
Слайд 18

Принадлежность прямой и точки плоскости
Точка принадлежит прямой, если ее проекции расположены
на одноименных проекциях этой прямой: А∈m, если А1∈m1; А2∈m2.
Точка принадлежит плоскости, если она расположена на прямой, принадлежащей этой
плоскости.
Прямая принадлежит плоскости, если она:
а) проходит через две точки, принадлежащие
этой плоскости;
б) проходит через точку плоскости и
параллельна линии, лежащей в этой плоскости.
Слайд 19
Слайд 20

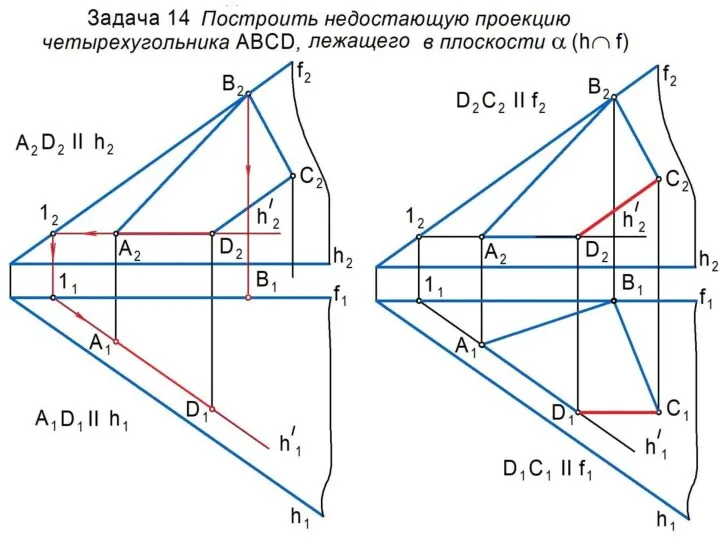
Главные линии плоскости
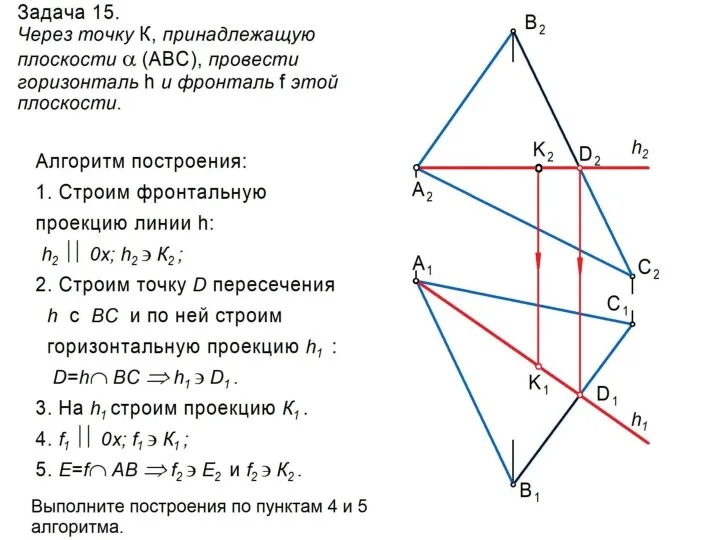
Горизонталь h – это линия, принадлежащая
плоскости α и параллельная
П1 . Ее фронтальная проекция параллельна оси 0х:
h ⊂ α; h II П1 ⇒ h2 II 0х.
Фронталь f – это линия, принадлежащая
плоскости α и параллельная П2 . Ее горизонтальная проекция параллельна оси 0х:
f ⊂ α; f II П2 ⇒ f1 II 0х.
Слайд 21
Слайд 22

Алгоритм задачи на пересечение двух плоскостей
Задан эпюр двух плоскостей α и
β.
Необходимо построить их линию пересечения l = α∩β .
При решении задач НГ на пересечение геометрических фигур используют посредники, чаще всего таковыми являются проецирующие плоскости.
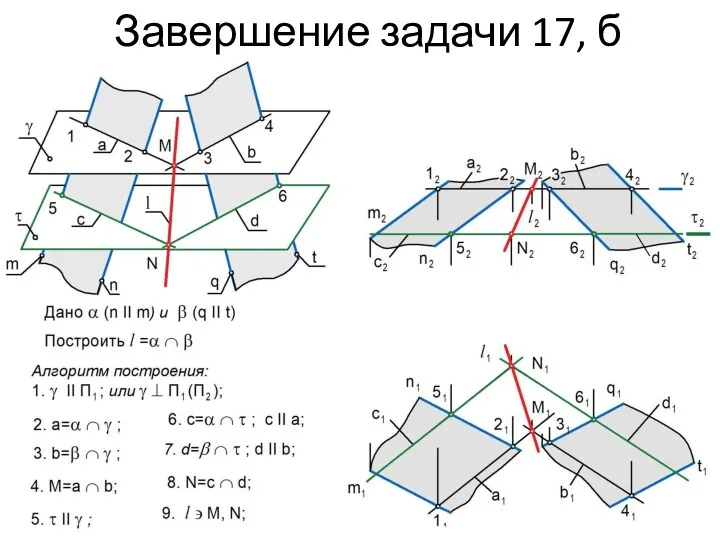
1. Строим вспомогательную проецирующую плоскость γ, которая пересекает плоскость α по прямой a , а плоскость β – по прямой b. Поскольку обе указанные прямые лежат в плоскости γ , то пересекаясь они образуют точку М, принадлежащую искомой линии.
2. Для нахождения второй точки N cтроим новую вспомогательную проецирующую плоскость τ. Далее строим:
с = τ ∩ α; d = τ ∩ β; N = c ∩ d.
3. Через точки M и N проводим искомую линию l.
Слайд 23
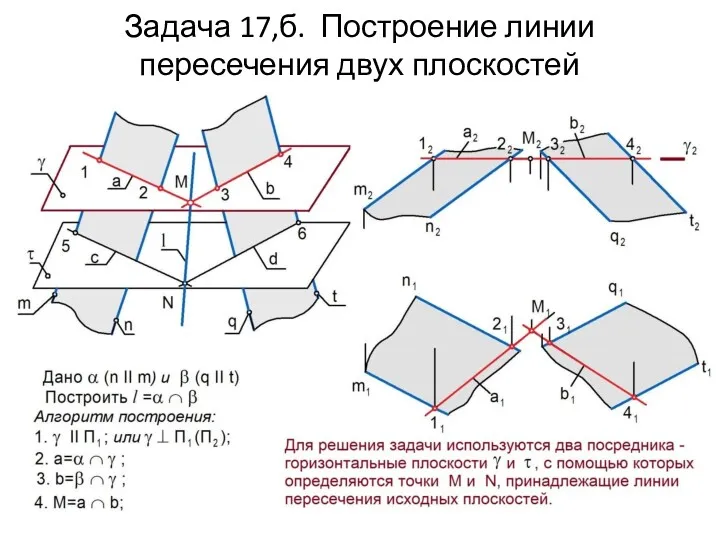
Задача 17,б. Построение линии пересечения двух плоскостей
Слайд 24
Слайд 25
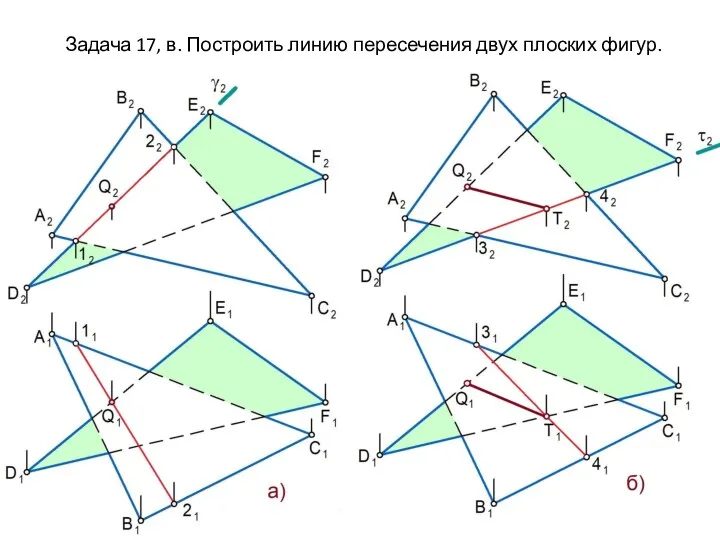
Задача 17, в. Построить линию пересечения двух плоских фигур.
Слайд 26
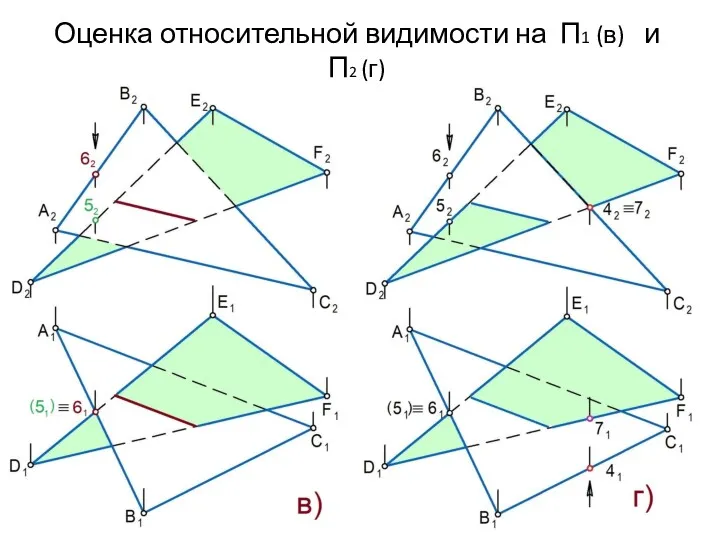
Оценка относительной видимости на П1 (в) и П2 (г)
Слайд 27

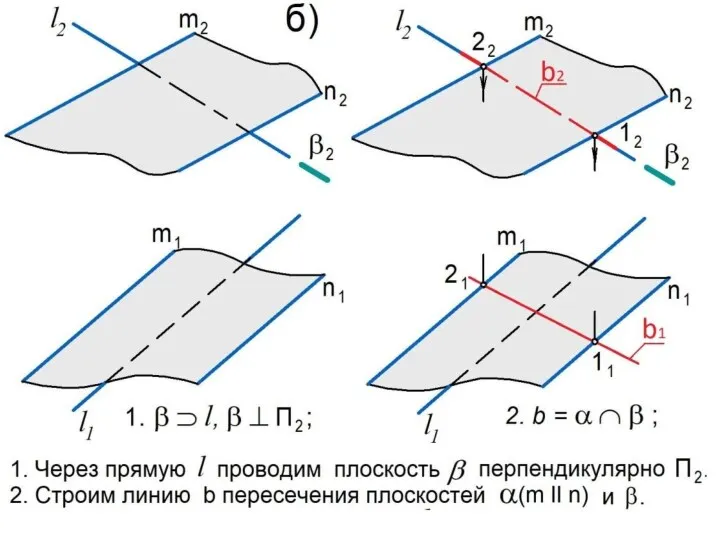
Алгоритм задачи на пересечение прямой и плоскости
Задан эпюр плоскости α
общего положения и прямой l .
Необходимо построить точку К их пересечения: К = α ∩ l.
1. Через прямую l проводим вспомогательную проецирующую
плоскость β.
2. Строим прямую b - линию пересечения плоскостей α и β:
b = α ∩ β.
3. Находим искомую точку К, как результат пересечения прямых
l и b: K = l ∩ b.
4. Используя конкурирующие точки, разграничиваем видимость
прямой l относительно плоскости α.
Слайд 28

Построить точку пересечения прямой l с плоскостью α(ABC)
Слайд 29
Слайд 30

Слайд 31

Перпендикуляр к плоскости
Общее геометрическое определение.
Прямая перпендикулярна плоскости, если она перпендикулярна двум
пересекающимся прямым этой плоскости.
Определение для НГ.
Прямая n перпендикулярна плоскости α, если она
одновременно перпендикулярна ее горизонталям h и фронталям f:
n⊥α, если а) n ⊥ h ⇒ n1 ⊥ h1;
б) n ⊥ f ⇒ n2 ⊥ f2.
Слайд 32

Задача 19. Определить расстояние от точки А до плоскости α (DEF)
Слайд 33

Слайд 34

Определения взаимно перпендикулярных плоскостей
Определение 1. Две плоскости взаимно перпендикулярны, если одна
из них проходит через перпендикуляр к другой плоскости.
Определение 2. Две плоскости взаимно перпендикулярны, если одна из них перпендикулярна линии, принадлежащей другой плоскости.
Слайд 35


































 Урок математики в 4 классе Решение задач на движение
Урок математики в 4 классе Решение задач на движение Числительное в русском языке и математике. Виртуальная экскурсия по родному селу
Числительное в русском языке и математике. Виртуальная экскурсия по родному селу Математика. Поточная практика 7.1. Аналитическая геометрия. Прямая на плоскости
Математика. Поточная практика 7.1. Аналитическая геометрия. Прямая на плоскости Конспект с презентацией
Конспект с презентацией Таблица умножения. Интерактивный тренажёр
Таблица умножения. Интерактивный тренажёр Средства измерений и их классификация. Лекция 7
Средства измерений и их классификация. Лекция 7 Парадокс Гиффена
Парадокс Гиффена Ключевые задачи в процессе обучения школьников решению задач по геометрии
Ключевые задачи в процессе обучения школьников решению задач по геометрии Correlation Analysis and Covariance
Correlation Analysis and Covariance Осевая и центральная симметрия 8 класс
Осевая и центральная симметрия 8 класс Первый признак равенства треугольников, часть 2
Первый признак равенства треугольников, часть 2 Возведение в степень произведения и степени
Возведение в степень произведения и степени Позиционные задачи начертательной геометрии
Позиционные задачи начертательной геометрии Свойства вычитания
Свойства вычитания Применение интеграла к решению задач
Применение интеграла к решению задач Презентация по теме: Многоугольники 2 класс.( Программа Начальная школа XXI века)
Презентация по теме: Многоугольники 2 класс.( Программа Начальная школа XXI века) Высказывание. Логические операции
Высказывание. Логические операции 20231024_prezentatsiya_znatoki_matematiki._tablitsa_umnozheniya
20231024_prezentatsiya_znatoki_matematiki._tablitsa_umnozheniya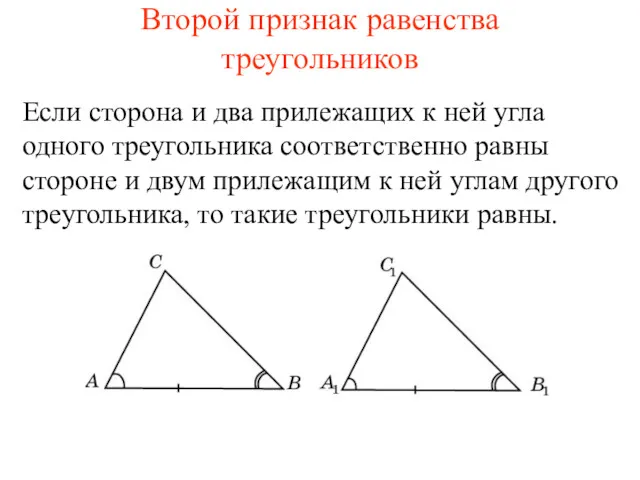 Второй признак равенства треугольников
Второй признак равенства треугольников Способы определения понятий
Способы определения понятий Задачи: условие, требование, решение
Задачи: условие, требование, решение Урок математики 1класс. Точки и линии
Урок математики 1класс. Точки и линии Буратино в стране математики
Буратино в стране математики Умножение числа 2 и на 2
Умножение числа 2 и на 2 Интерактивное пособие для подготовки к ОГЭ. Окружность
Интерактивное пособие для подготовки к ОГЭ. Окружность Игра по математике Своя игра
Игра по математике Своя игра Математикалық талдау
Математикалық талдау Смежные и вертикальные углы
Смежные и вертикальные углы