Содержание
- 2. ДВУГРАННЫЙ УГОЛ ОПРЕДЕЛЕНИЕ: Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей
- 3. ОПРЕДЕЛЕНИЕ: Линейный угол -- угол, стороны которого являются лучами, перпендикулярными к ребру двугранного угла, а вершина
- 4. В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ: 90o. Упражнение
- 5. В кубе A…D1 найдите угол между плоскостями ABC и CDA1. Ответ: 45o. Упражнение
- 6. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Две плоскости называются перпендикулярными, если угол между ними прямой.
- 7. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ : Если одна из двух плоскостей проходит через прямую, перпендикулярную к
- 8. ДОКАЗАТЕЛЬСТВО 1) АВ ⊥ β, АС ⊂ β => АВ ⊥ АС (α ∩ β =
- 9. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ СЛЕДСТВИЕ ИЗ ПРИЗНАКА ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ: Плоскость, перпендикулярная к прямой, по которой пересекаются две данные
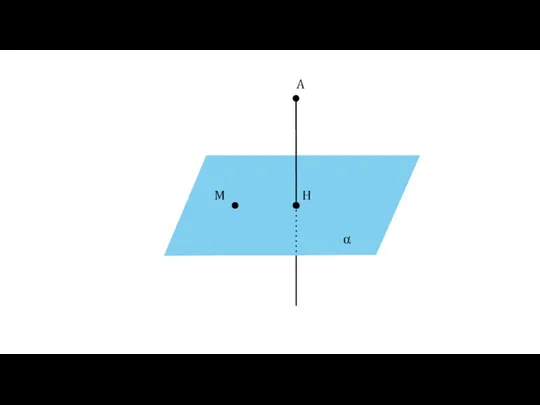
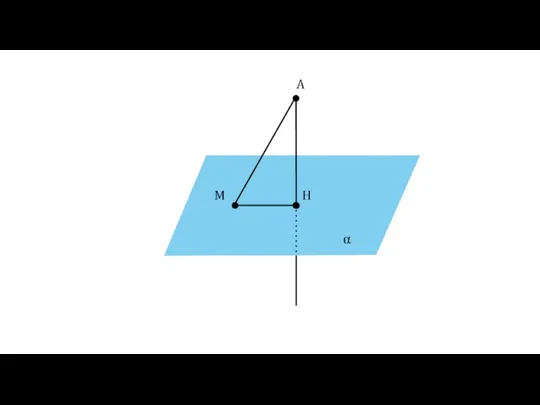
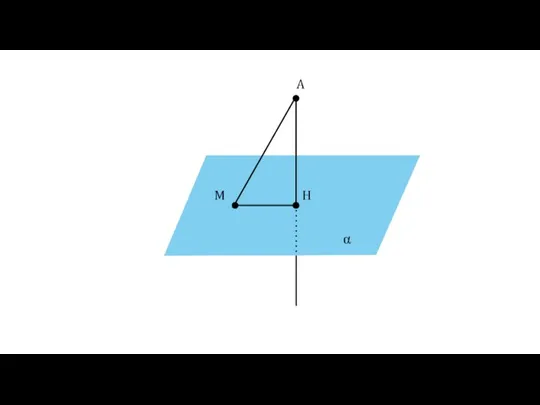
- 10. Определение Перпендикуляром, проведённым из точки А к плоскости α, называется отрезок АН. Точка Н называется основанием
- 11. α A H M
- 12. α A H M
- 13. α A H M
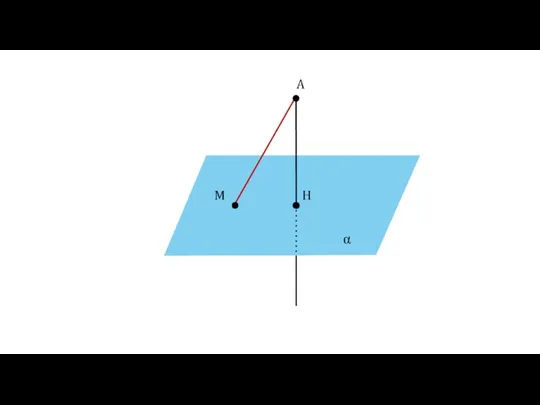
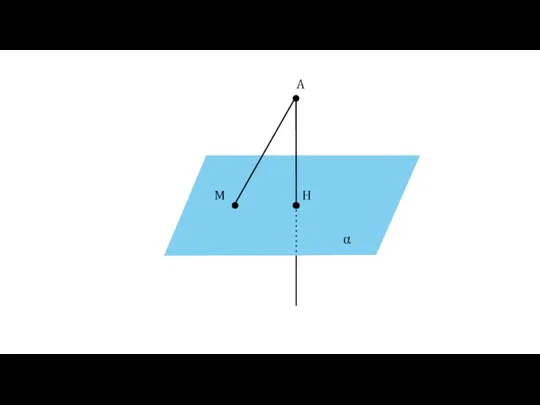
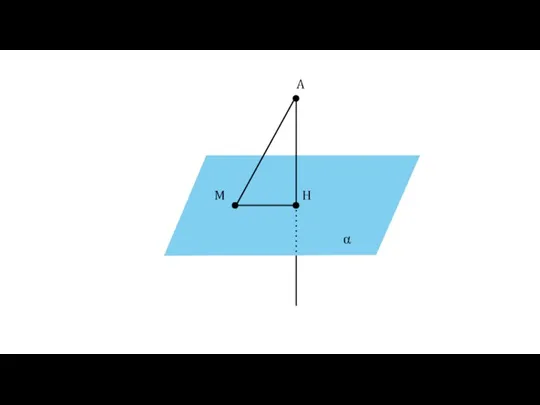
- 14. Определение Отрезок АМ называется наклонной, проведённой из точки А к плоскости α. Точка М называется основанием
- 15. α A H M
- 16. α A H M
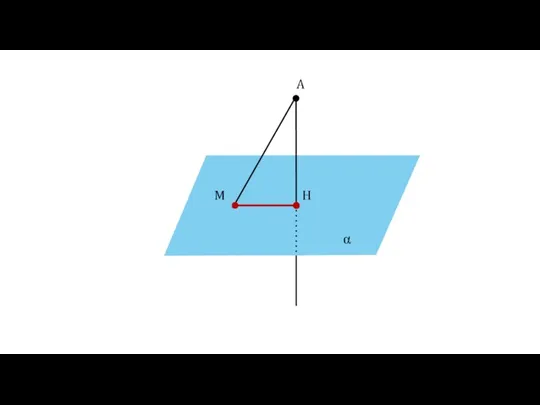
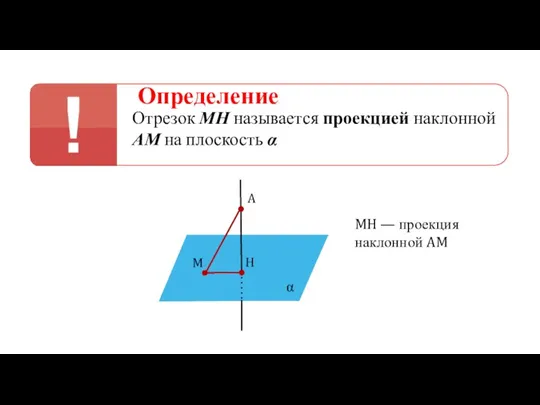
- 17. Определение Отрезок МН называется проекцией наклонной АМ на плоскость α α A H M MH —
- 18. α A H M
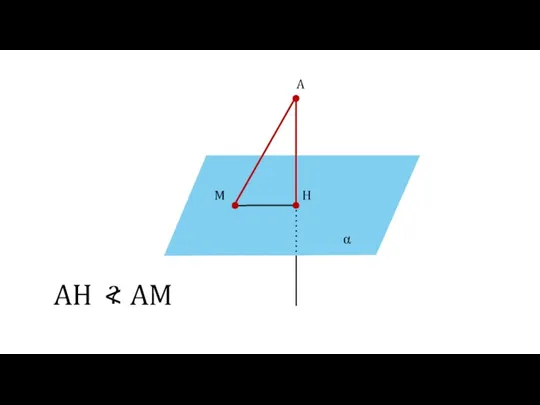
- 19. α A H M AH AM ?
- 20. α A H M
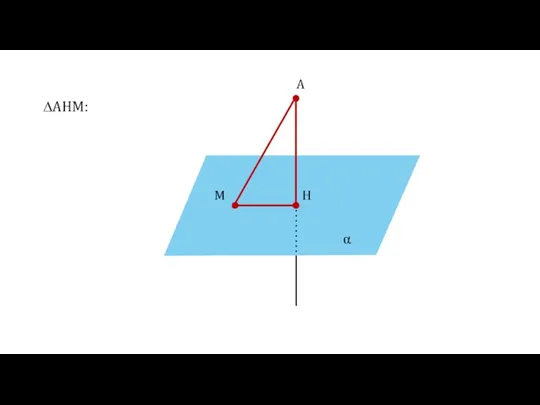
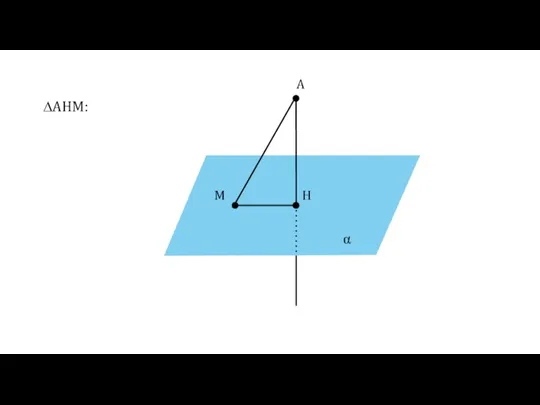
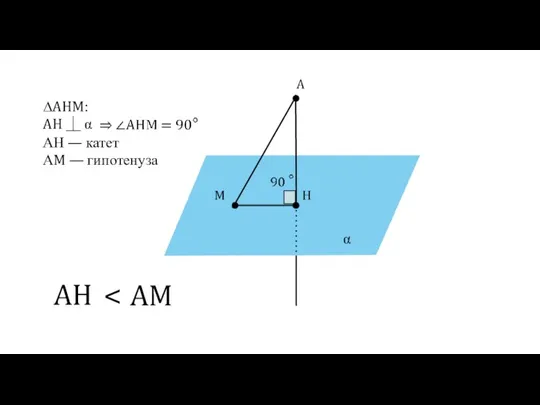
- 21. α A H M ∆AHM:
- 22. α A H M ∆AHM:
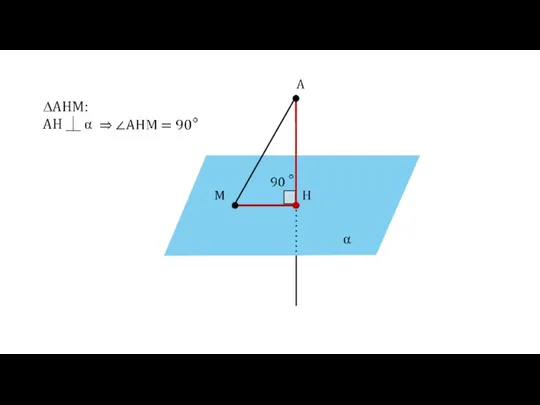
- 23. α A H M ∆AHM: AH ⏊ α
- 24. α A H M ∆AHM: AH ⏊ α AH AM АН — катет АM — гипотенуза
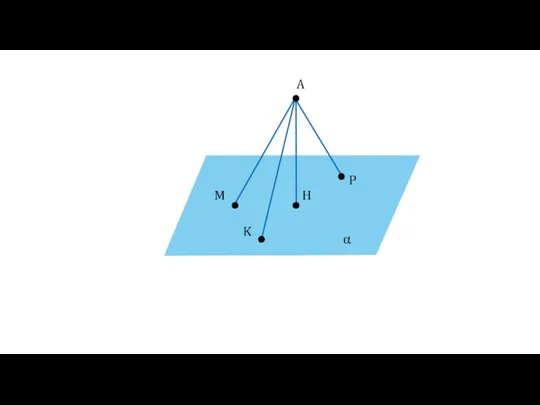
- 25. α A H M P K
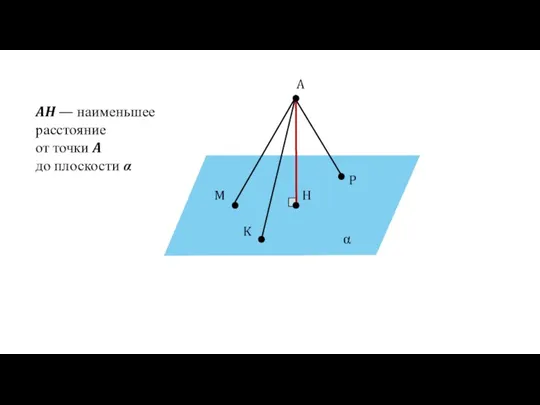
- 26. α A H M P K AH — наименьшее расстояние от точки A до плоскости α
- 27. Определение Расстоянием от точки А до плоскости α называется длина перпендикуляра АН, проведённого к плоскости α
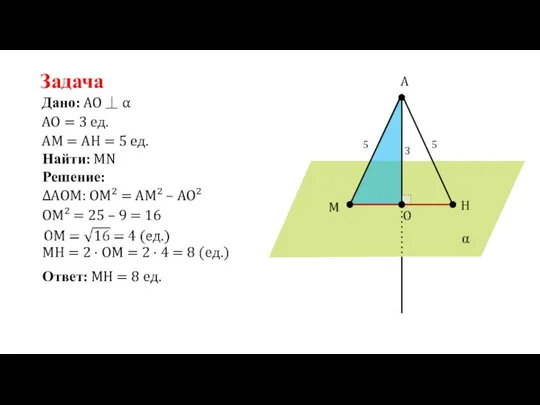
- 28. Задача Дано: AO = 3 ед. AO ⏊ α α A O M H 3 AM
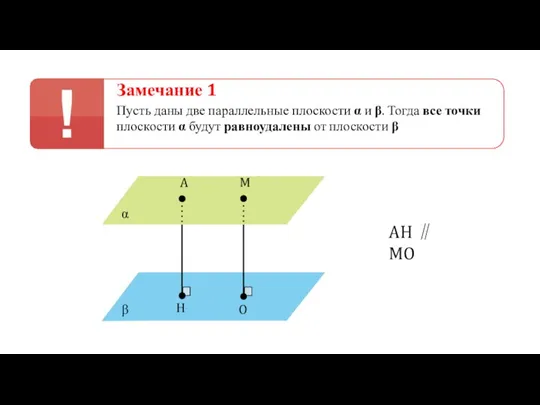
- 29. Замечание 1 Пусть даны две параллельные плоскости α и β. Тогда все точки плоскости α будут
- 30. Замечание 1 Пусть даны две параллельные плоскости α и β. Тогда все точки плоскости α будут
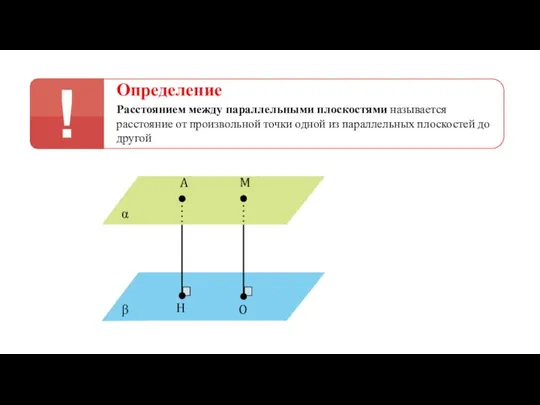
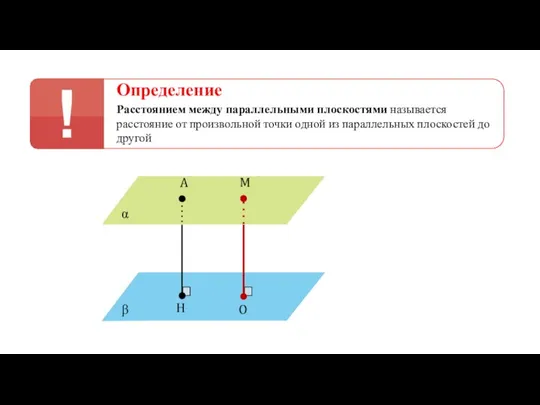
- 31. Определение Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой
- 32. Определение Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой
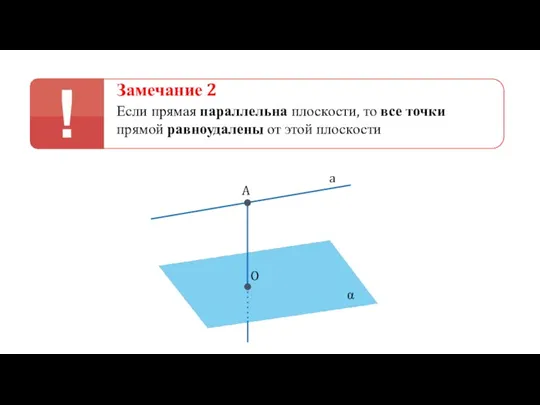
- 33. Замечание 2 Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости a A
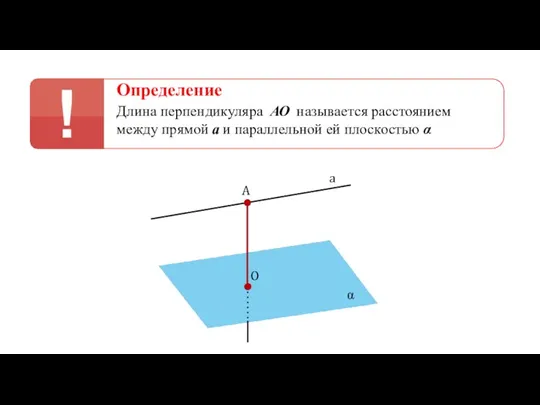
- 34. Определение Длина перпендикуляра АО называется расстоянием между прямой а и параллельной ей плоскостью α a A
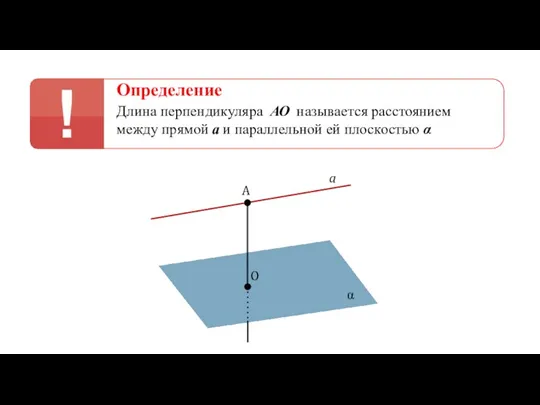
- 35. Определение Длина перпендикуляра АО называется расстоянием между прямой а и параллельной ей плоскостью α a A
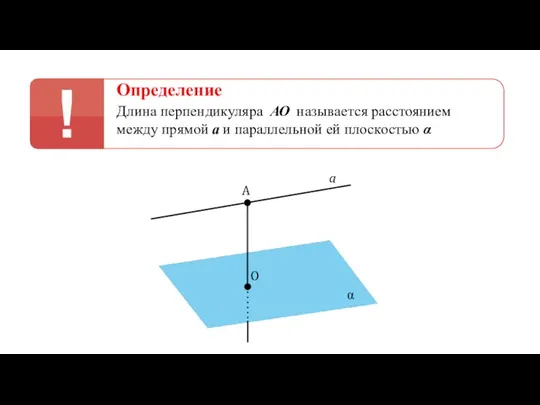
- 36. Определение Длина перпендикуляра АО называется расстоянием между прямой а и параллельной ей плоскостью α a A
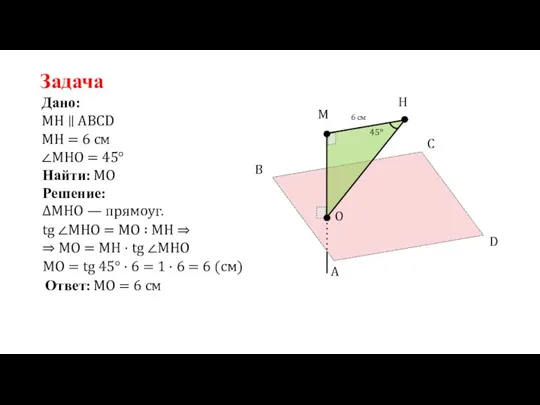
- 37. A Задача Дано: МН ∥ ABCD H M O B C D МН = 6 см
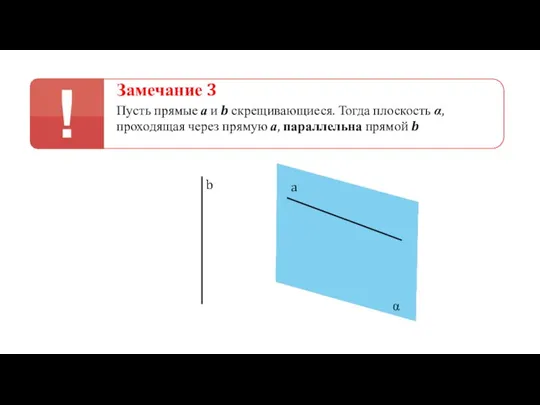
- 38. Замечание 3 Пусть прямые а и b скрещивающиеся. Тогда плоскость α, проходящая через прямую а, параллельна
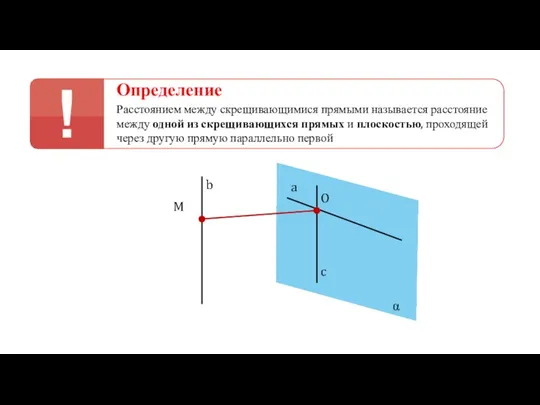
- 39. Определение Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через
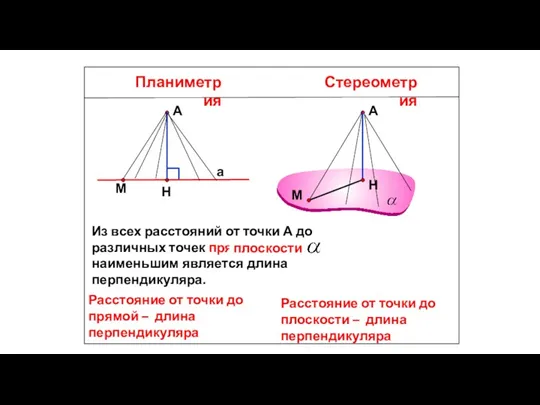
- 40. Планиметрия Стереометрия Расстояние от точки до прямой – длина перпендикуляра А а А Расстояние от точки
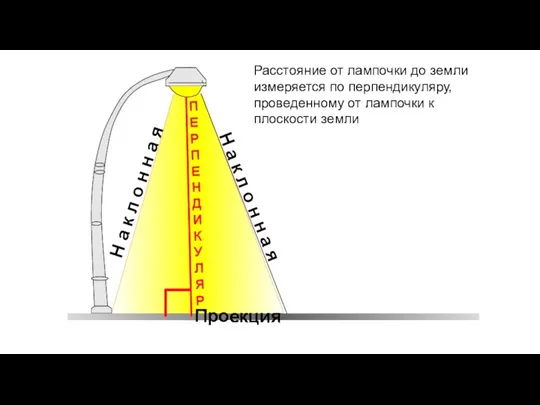
- 41. Расстояние от лампочки до земли измеряется по перпендикуляру, проведенному от лампочки к плоскости земли Н а
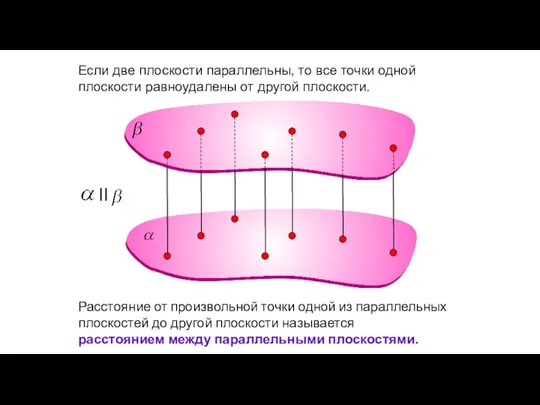
- 42. Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Расстояние от произвольной
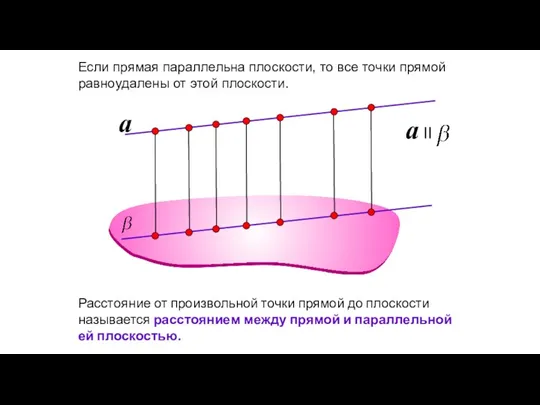
- 43. Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. a Расстояние от произвольной
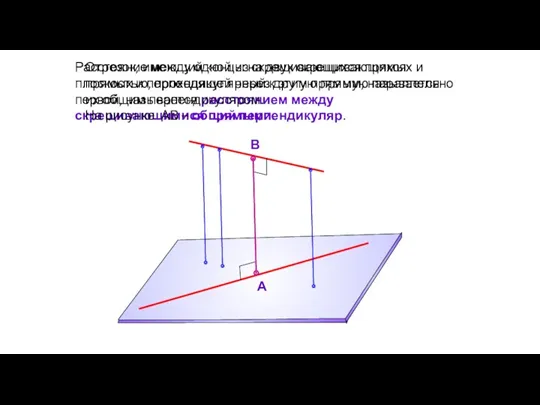
- 44. Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом
- 45. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием
- 46. В
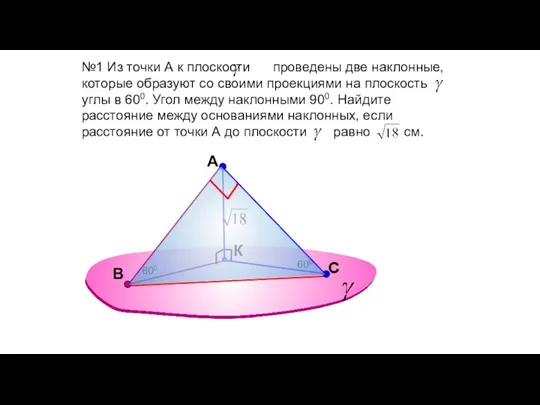
- 47. A К №1 Из точки А к плоскости проведены две наклонные, которые образуют со своими проекциями
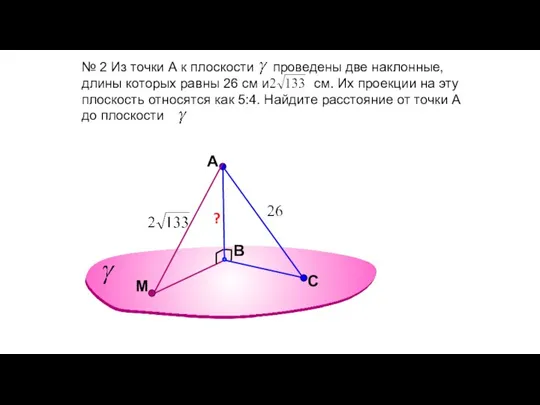
- 48. A В № 2 Из точки А к плоскости проведены две наклонные, длины которых равны 26
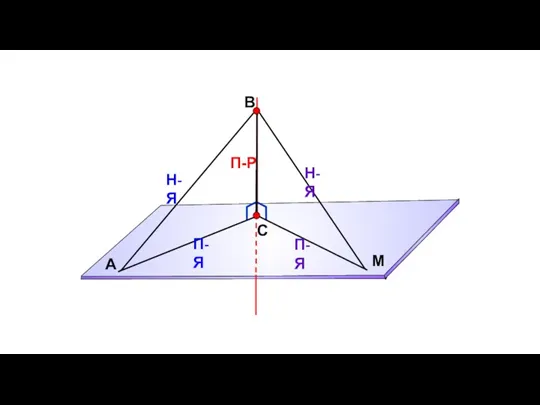
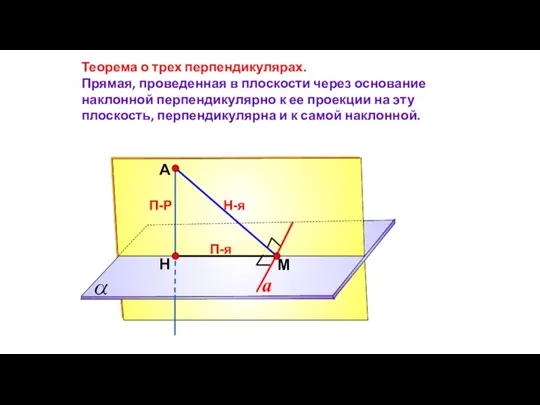
- 49. А Н П-Р М Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно
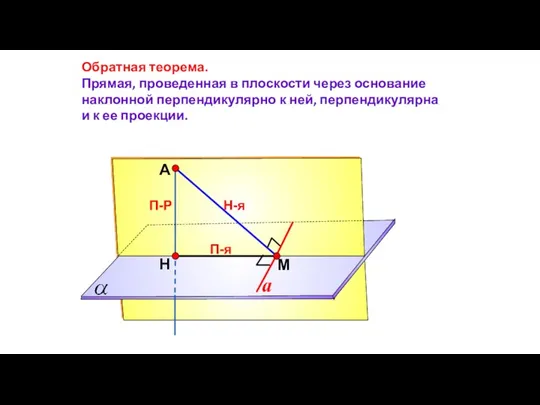
- 50. А Н П-Р М Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней,
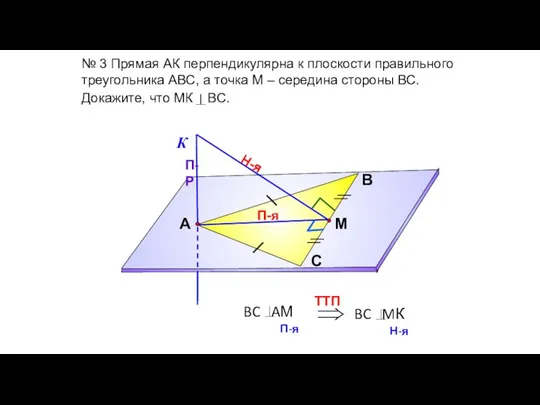
- 51. № 3 Прямая АК перпендикулярна к плоскости правильного треугольника АВС, а точка М – середина стороны
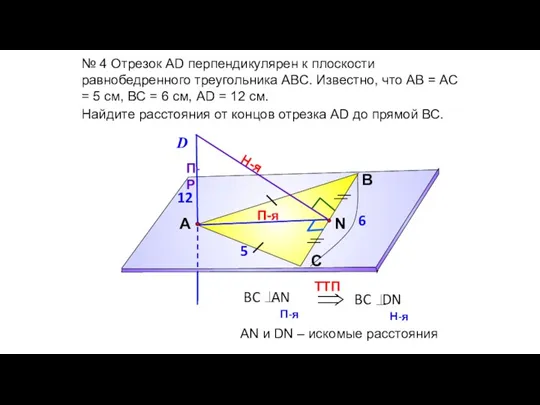
- 52. № 4 Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ = АС =
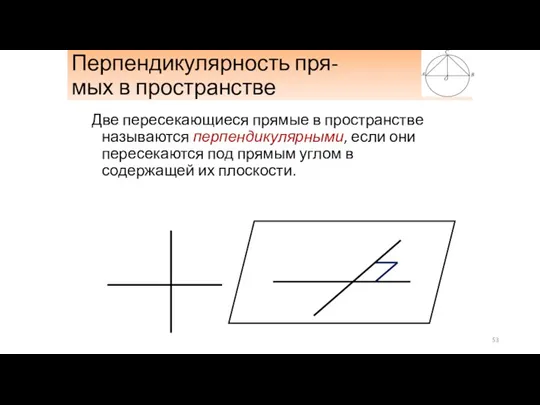
- 53. Перпендикулярность пря- мых в пространстве Две пересекающиеся прямые в пространстве называются перпендикулярными, если они пересекаются под
- 54. Перпендикулярные прямые Две скрещивающиеся прямые называются перпендикулярными, если параллельные им пересекающиеся прямые перпендикулярны. А b b’
- 55. Пример Назовите все прямые, перпендикулярные AD.
- 56. Вопрос Как показать, что прямые АС и B’D’ перпендикулярны?
- 57. Теорема Если две пересекающиеся прямые соответственно параллельны двум перпендикулярным прямым, то они тоже перпендикулярны. Доказательство в
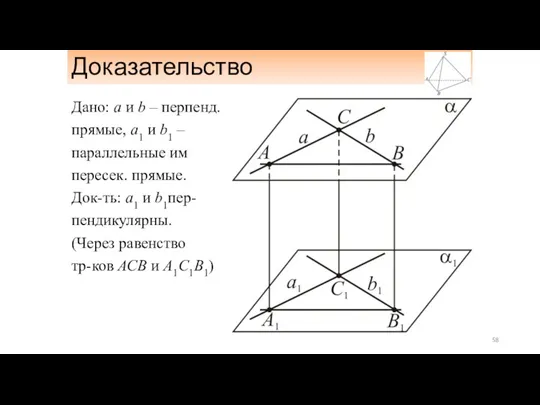
- 58. Доказательство Дано: а и b – перпенд. прямые, а1 и b1 – параллельные им пересек. прямые.
- 59. 1. Задача на построение Можно ли через любую точку прямой в пространстве провести перпендикулярную ей прямую?
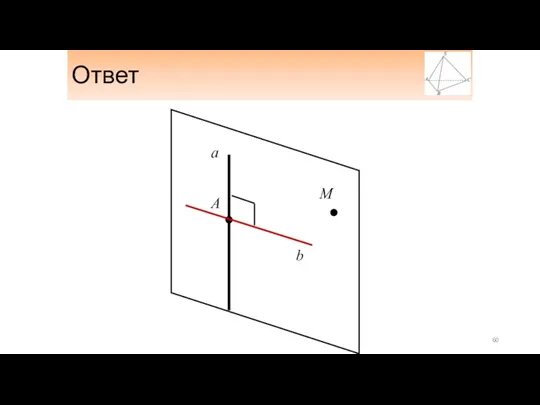
- 60. Ответ М А b а
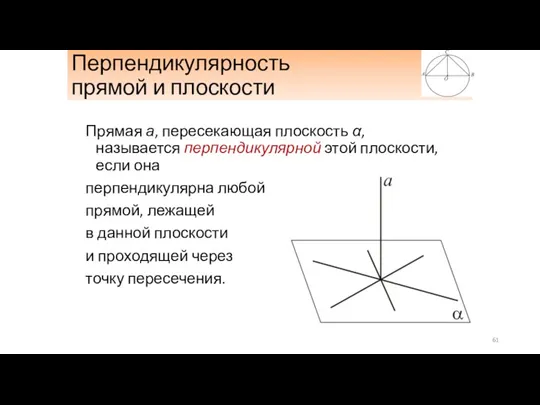
- 61. Перпендикулярность прямой и плоскости Прямая а, пересекающая плоскость α, называется перпендикулярной этой плоскости, если она перпендикулярна
- 62. Перпендикулярность прямой и плоскости Прямая а и плоскость β в пространстве называются перпендикулярными, если прямая а
- 63. Перпендикулярность прямой и плоскости обозначается знаком .
- 64. Признак перпендикулярности прямой и плоскости Если две пересекающие прямые, лежащие в плоскости β, перпендикулярны прямой а,
- 65. Свойства перпендикулярной прямой и плоскости Т.1. Если плоскость перпендикулярна одной из двух парал- лельных прямых, то
- 66. Свойства перпендикулярной прямой и плоскости Т.1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она
- 67. Свойства перпендикулярной прямой и плоскости Т.2. Две прямые, пер- пендикулярные одной и той же плоскости, параллельны.
- 68. Теорема 3. Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости.
- 69. Обратное утверждение Верно обратное свойство. Если прямая перпендикулярна двум различным плоскостям, то эти плоскости параллельны.
- 70. Теорема о трех перпендикулярах Прямая теорема. Прямая, проведенная на плоскости через основание наклон- ной перпендикулярно ее
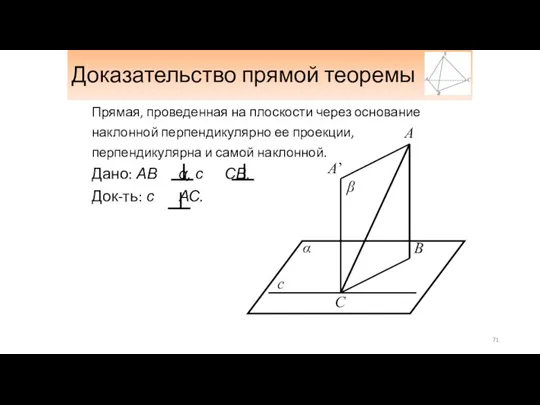
- 71. Доказательство прямой теоремы Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой
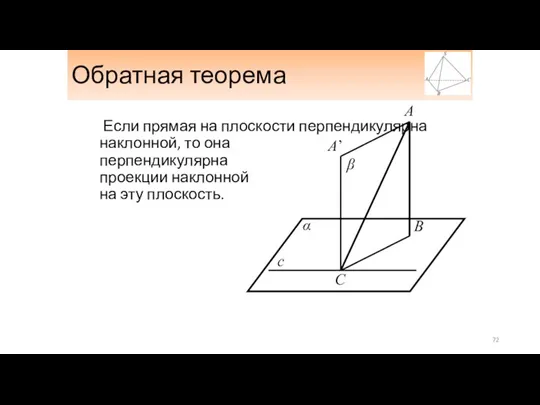
- 72. Обратная теорема Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна проекции наклонной на эту плоскость.
- 73. Перпендикулярность плоскостей Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересече- ния этих плос-
- 74. Утверждение Любая плоскость, перпендикулярная прямой пересечения перпендикулярных плоскостей, пересекает их по перпендикулярным прямым.
- 75. Признак перпендикуляр- ности плоскостей Теорема. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости
- 76. Теорема о прямой, перпендикулярной линии пересечения двух взаимно перпендикулярных плоскостей Если в одной из двух перпендикулярных
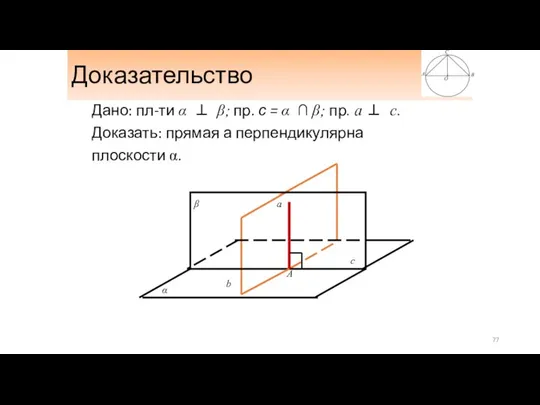
- 77. Доказательство Дано: пл-ти α ⊥ β; пр. с = α ∩ β; пр. а ⊥ с.
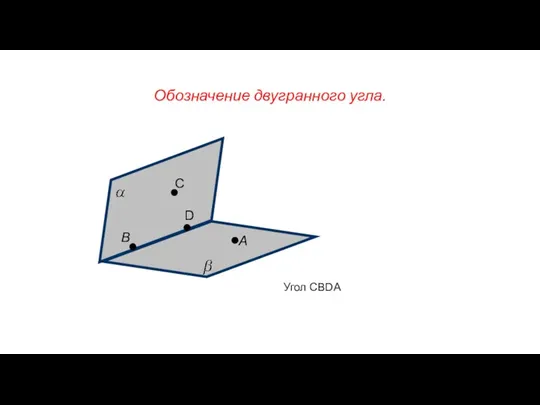
- 78. Обозначение двугранного угла. А В С D Угол CBDA
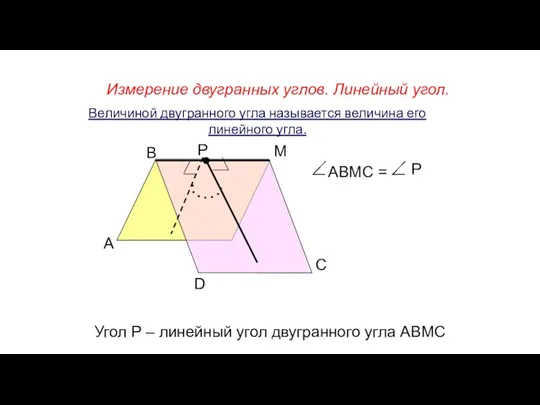
- 79. Измерение двугранных углов. Линейный угол. А В М D Р С АВМС = Р Угол Р
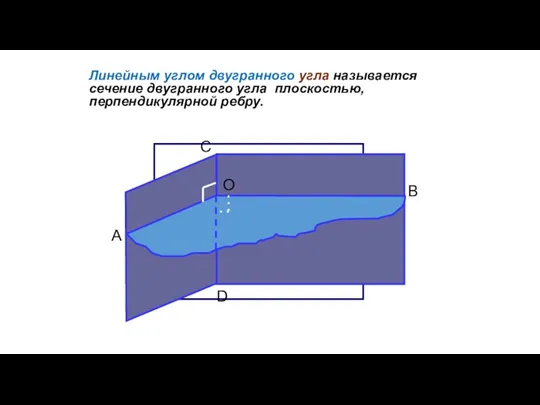
- 80. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
- 81. Способ нахождения (построения) линейного угла. 1. Найти ( увидеть) ребро и грани двугранного угла 2. В
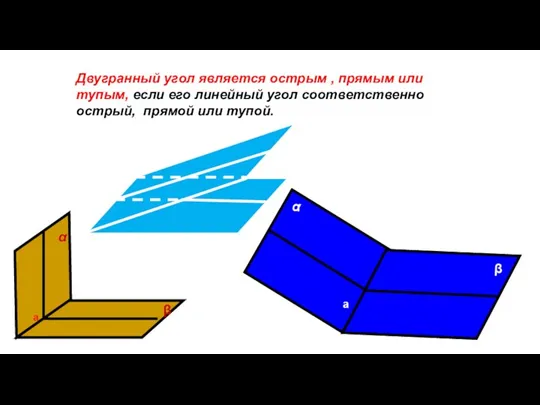
- 82. Двугранный угол является острым , прямым или тупым, если его линейный угол соответственно острый, прямой или
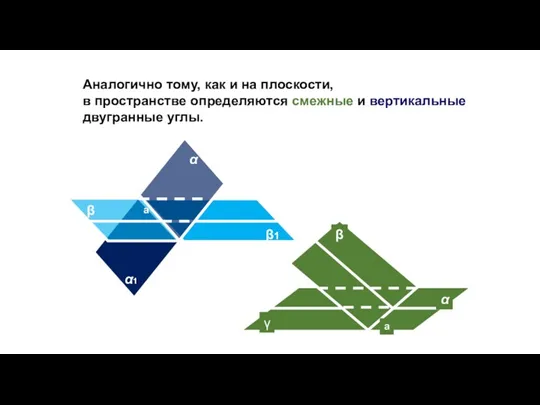
- 83. Аналогично тому, как и на плоскости, в пространстве определяются смежные и вертикальные двугранные углы. β β1
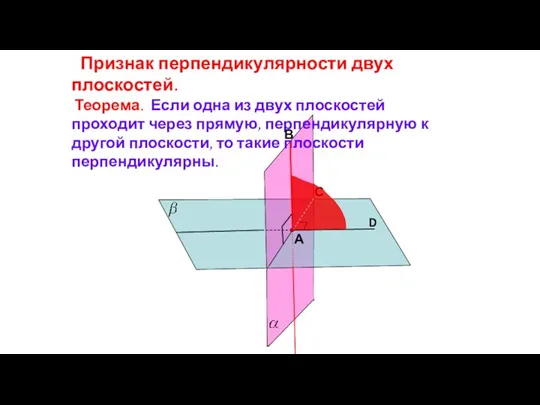
- 84. Признак перпендикулярности двух плоскостей. Теорема. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой
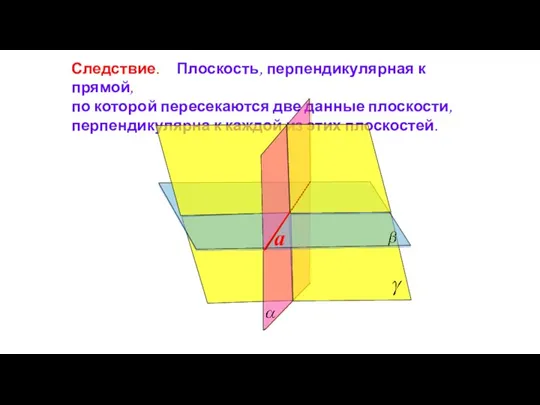
- 85. Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих
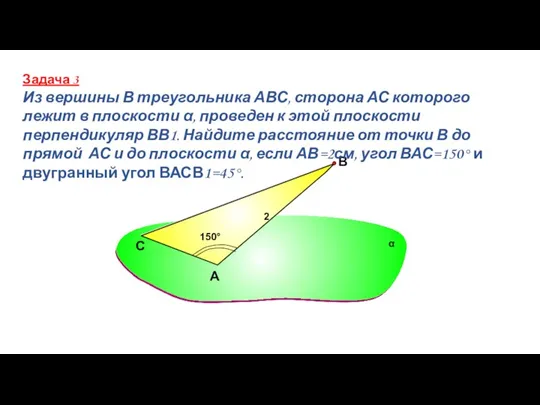
- 86. А В Задача 3 Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α,
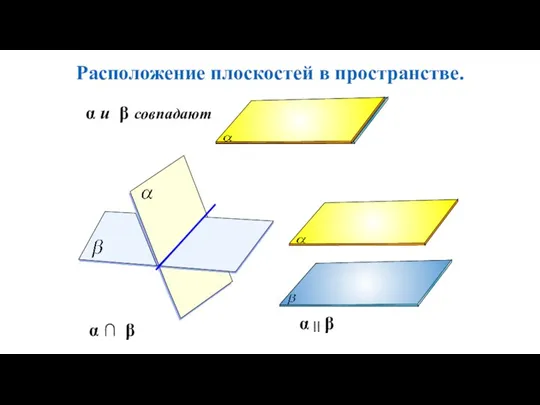
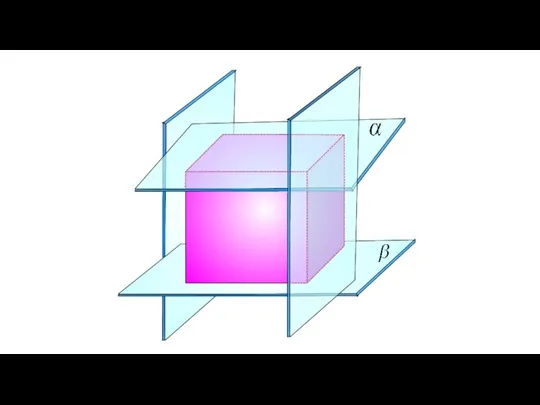
- 87. Расположение плоскостей в пространстве. α ∩ β α и β совпадают α ⎜⎜ β
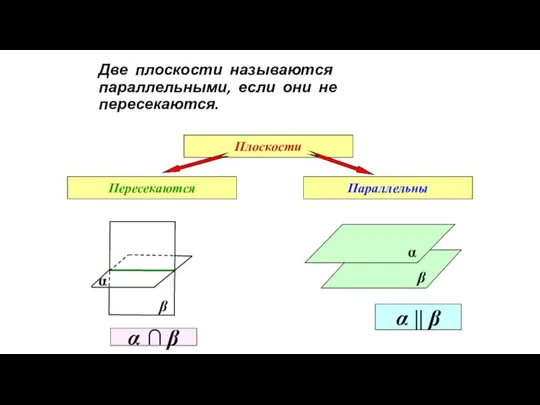
- 88. Две плоскости называются параллельными, если они не пересекаются. Плоскости Пересекаются Параллельны β α α || β
- 91. Признак параллельности плоскостей Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то
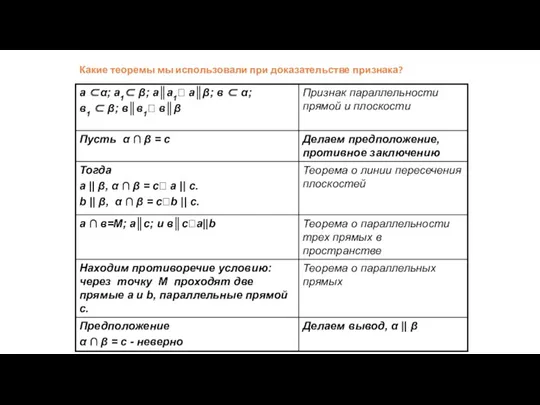
- 92. Доказательство от противного α β а b М b1 а1 М1 с а ⊂α; а1⊂ β;
- 93. Какие теоремы мы использовали при доказательстве признака?
- 94. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Свойство параллельных плоскостей. Дано: α
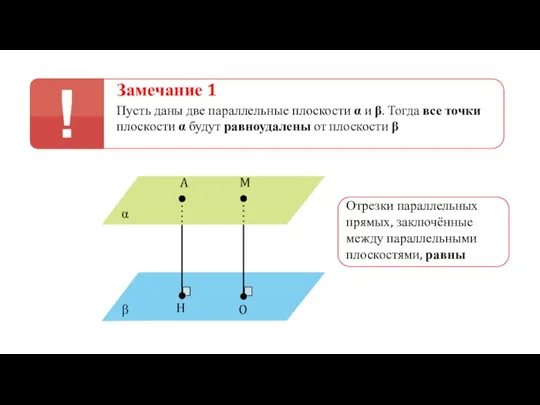
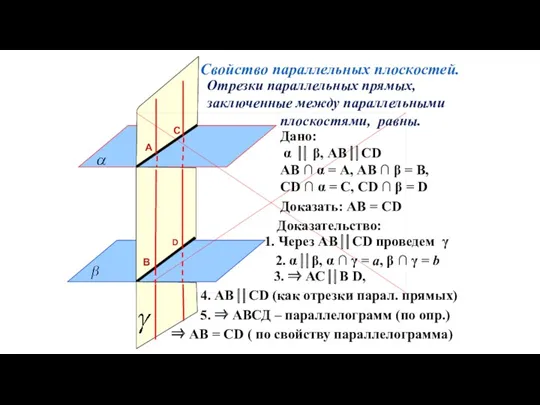
- 95. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. Свойство параллельных плоскостей. Доказать: АВ = СD Дано:
- 97. Доказать: β пересекается с γ Дано: α ⎜⎜ β, α пересекается с γ (рис) Доказательство: Пусть
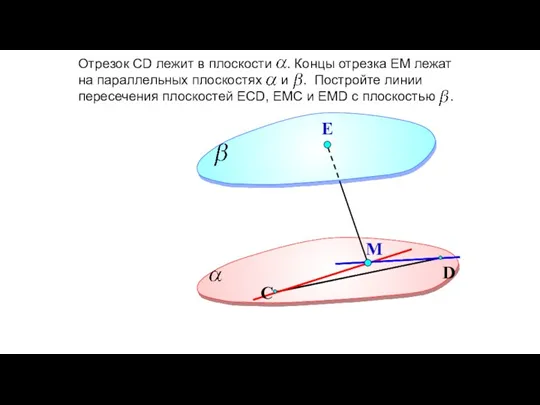
- 98. D Е М С
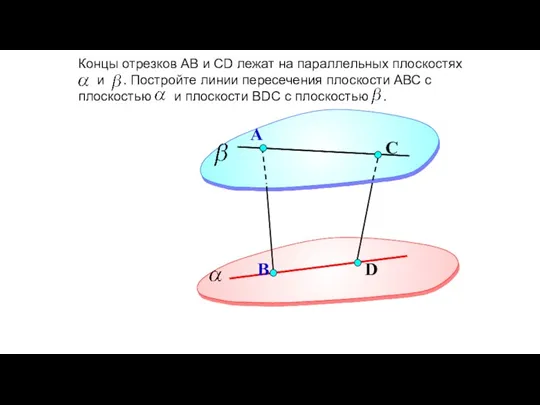
- 99. D А Концы отрезков АВ и СD лежат на параллельных плоскостях и . Постройте линии пересечения
- 100. D А В С
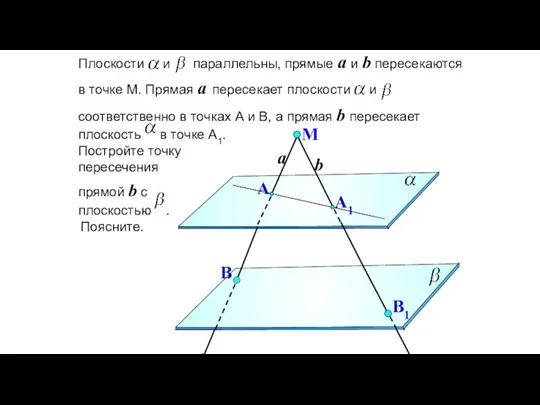
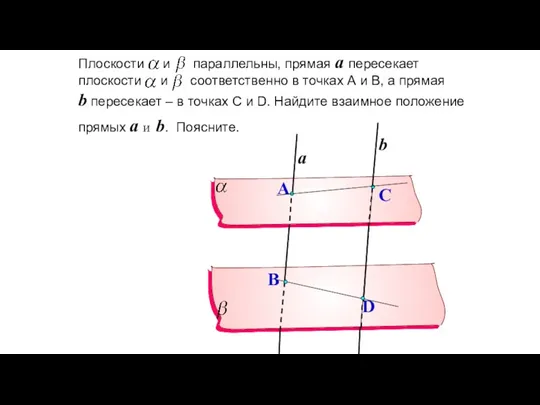
- 101. Плоскости и параллельны, прямые a и b пересекаются в точке М. Прямая a пересекает плоскости и
- 102. a a1 A A1 B
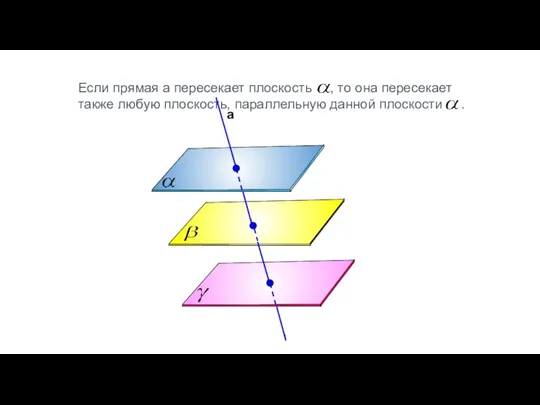
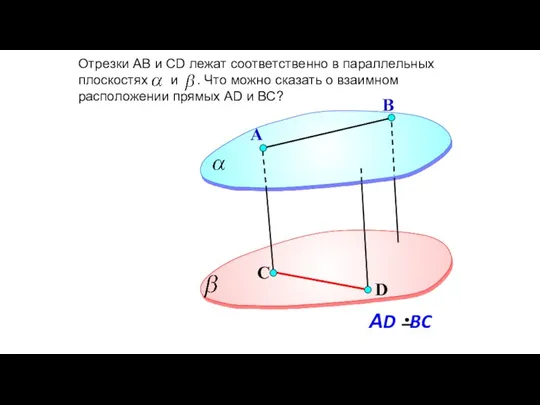
- 103. Плоскости и параллельны, прямая a пересекает плоскости и соответственно в точках А и В, а прямая
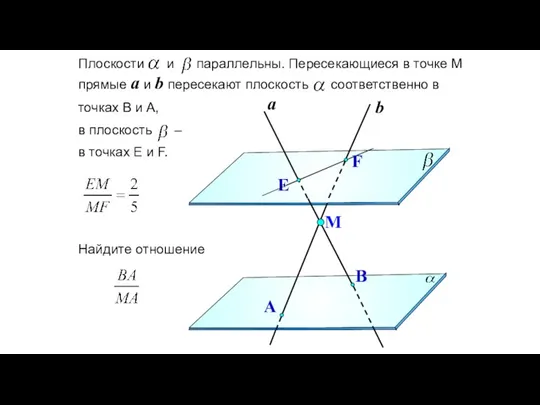
- 104. Плоскости и параллельны. Пересекающиеся в точке М прямые a и b пересекают плоскость соответственно в точках
- 105. Тетраэдр и параллелепипед
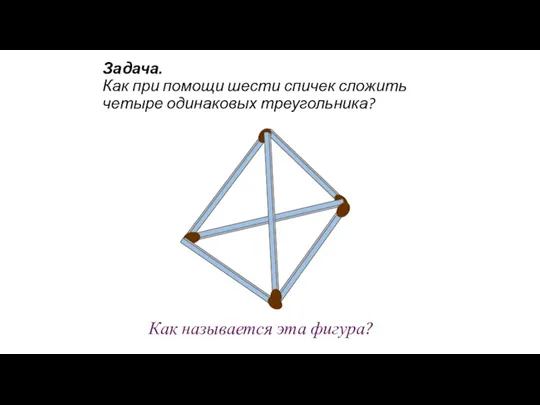
- 106. Задача 1 Как при помощи шести спичек сложить четыре одинаковых треугольника? Автор: Семёнова Елена Юрьевна МОУ
- 107. Задача. Как при помощи шести спичек сложить четыре одинаковых треугольника? Как называется эта фигура?
- 108. Тетраэдр
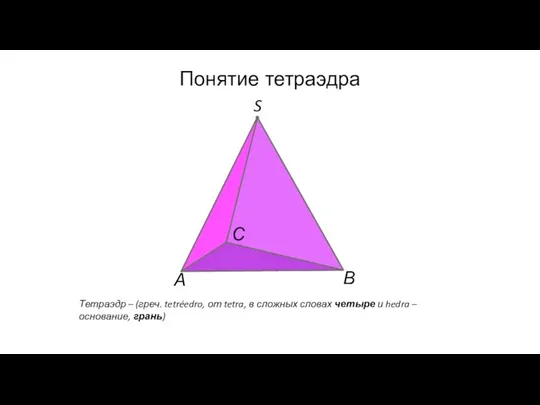
- 109. S Понятие тетраэдра А В С Тетраэдр – (греч. tetréedro, от tetra, в сложных словах четыре
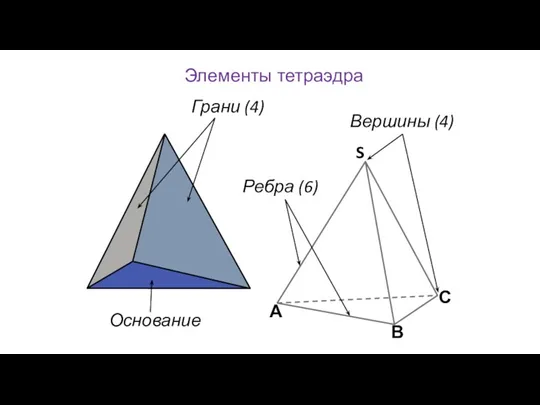
- 110. Элементы тетраэдра Грани (4) Ребра (6) Вершины (4) Основание
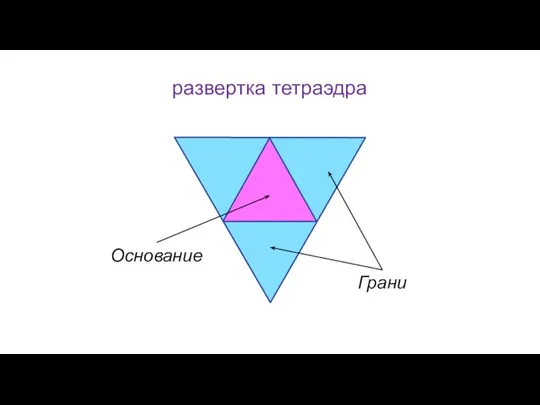
- 111. развертка тетраэдра Грани Основание
- 112. параллелепипед
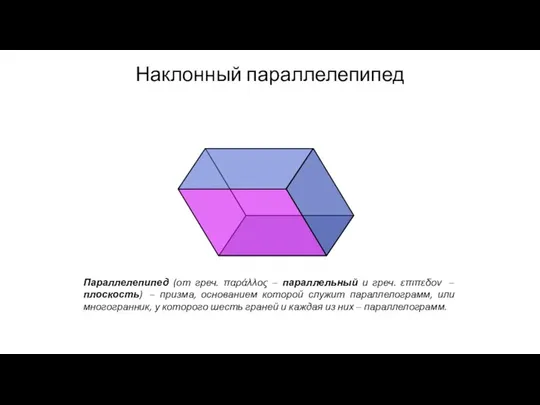
- 113. Наклонный параллелепипед Параллелепипед (от греч. παράλλος − параллельный и греч. επιπεδον − плоскость) − призма, основанием
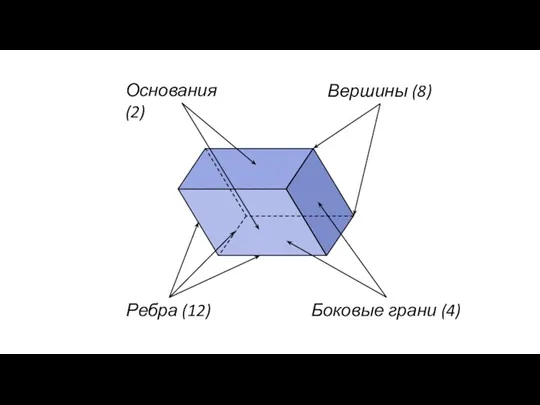
- 114. Ребра (12) Боковые грани (4) Вершины (8) Основания (2)
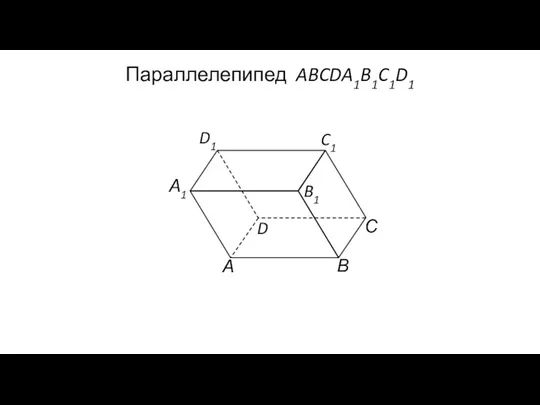
- 115. Параллелепипед ABCDA1B1C1D1
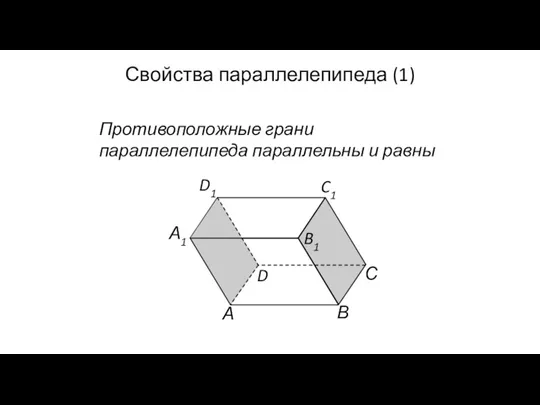
- 116. А В С А1 D D1 B1 C1 Свойства параллелепипеда (1) Противоположные грани параллелепипеда параллельны и
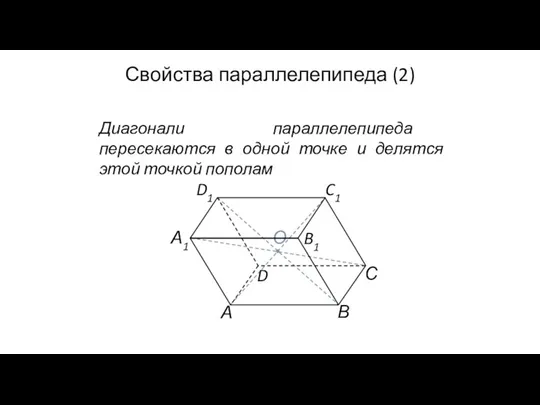
- 117. О Свойства параллелепипеда (2) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам
- 118. Прямой параллелепипед Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой параллелепипед называется прямым боковые грани
- 119. Прямоугольный параллелепипед Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным все грани – прямоугольники
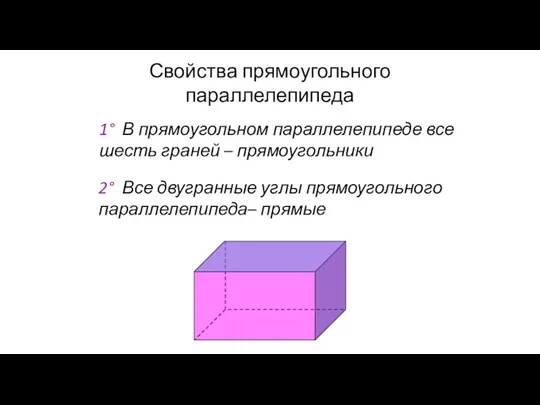
- 120. Свойства прямоугольного параллелепипеда 1° В прямоугольном параллелепипеде все шесть граней – прямоугольники 2° Все двугранные углы
- 121. Прямоугольный параллелепипед Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда длина, ширина и высота
- 123. Скачать презентацию












































 Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА
Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА Путешествие по Горному Алтаю. Проценты (интегрированный урок). 5 класс
Путешествие по Горному Алтаю. Проценты (интегрированный урок). 5 класс Полный факторный эксперимент
Полный факторный эксперимент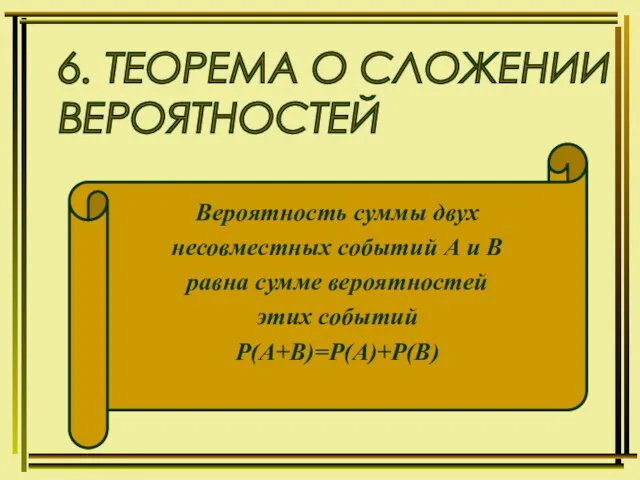 Теорема о сложении вероятностей
Теорема о сложении вероятностей Транспортные задачи
Транспортные задачи Сложение в столбик в пределах 100 (2класс)
Сложение в столбик в пределах 100 (2класс) Математика. 4 класс. Итоговое повторение (тест)
Математика. 4 класс. Итоговое повторение (тест) Решение неравенств методом интервалов
Решение неравенств методом интервалов Формулы сокращённого умножения. 7 класс
Формулы сокращённого умножения. 7 класс Экстремумы функции
Экстремумы функции Виды призм. Площадь поверхности призм
Виды призм. Площадь поверхности призм Центральная симметрия
Центральная симметрия Пространство. Трехмерное пространство
Пространство. Трехмерное пространство Случайная изменчивость
Случайная изменчивость Математическое моделирование. Значимость коэффициентов регрессии
Математическое моделирование. Значимость коэффициентов регрессии Случаи сложения вида +6
Случаи сложения вида +6 Подготовка учащихся к ОГЭ по математике
Подготовка учащихся к ОГЭ по математике Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Многочлен. Урок математики 7 класс
Многочлен. Урок математики 7 класс Умножение десятичных дробей
Умножение десятичных дробей Занимательная математика Геометрические фигуры
Занимательная математика Геометрические фигуры Средние величины
Средние величины Статистика по опросу студентов, проходивших практику
Статистика по опросу студентов, проходивших практику Математическая игра Магия чисел
Математическая игра Магия чисел Построение правильных многоугольников с помощью циркуля и линейки
Построение правильных многоугольников с помощью циркуля и линейки Определение геометрической прогрессии
Определение геометрической прогрессии Оценка статистических характеристик
Оценка статистических характеристик Игра Помоги поросятам спрятаться от волка
Игра Помоги поросятам спрятаться от волка