Содержание
- 2. План Лінійні операції над векторами Проекція вектора на вісь Лінійна залежність та незалежність векторів Метод координат
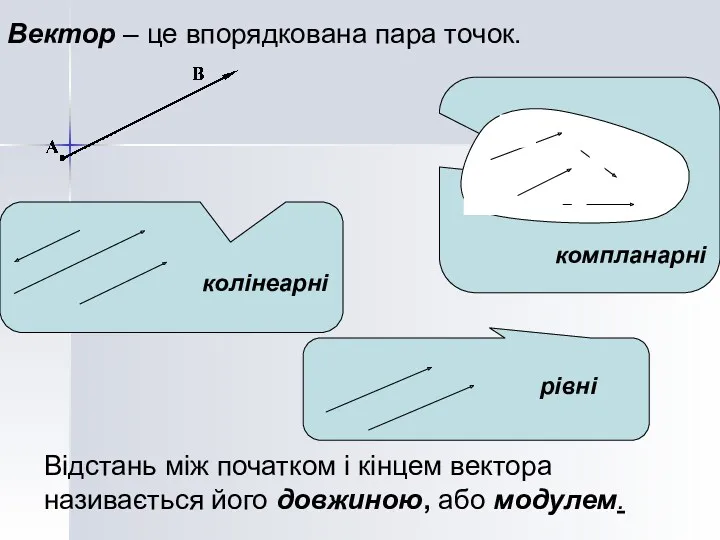
- 3. Вектор – це впорядкована пара точок. Відстань між початком і кінцем вектора називається його довжиною, або
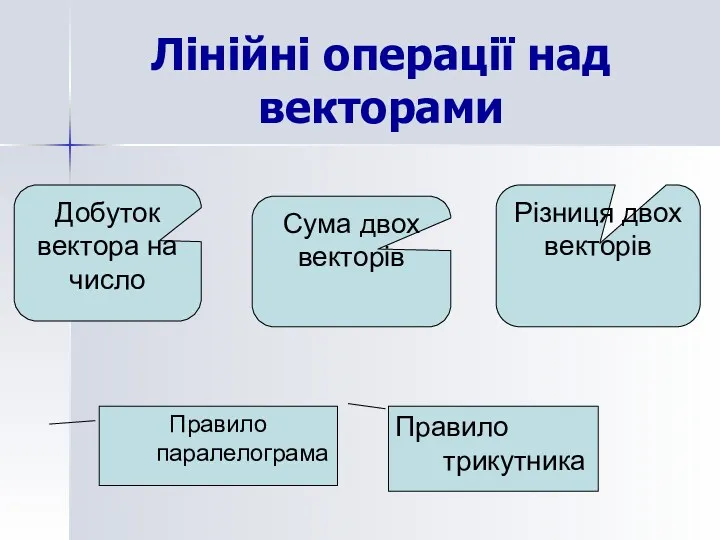
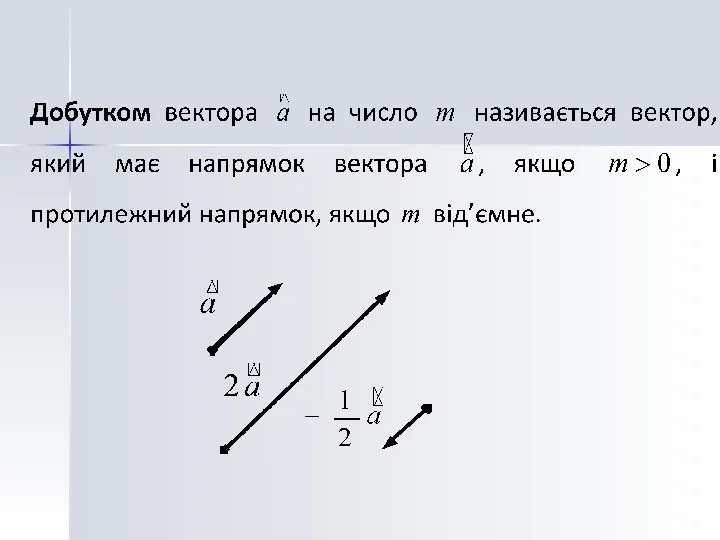
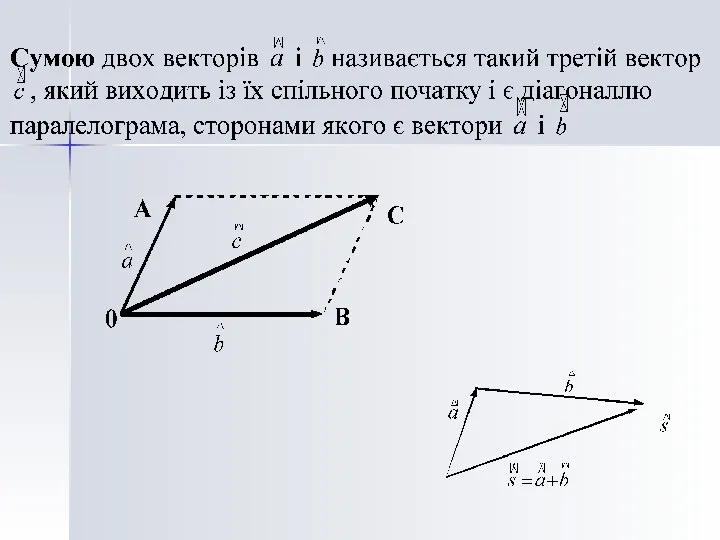
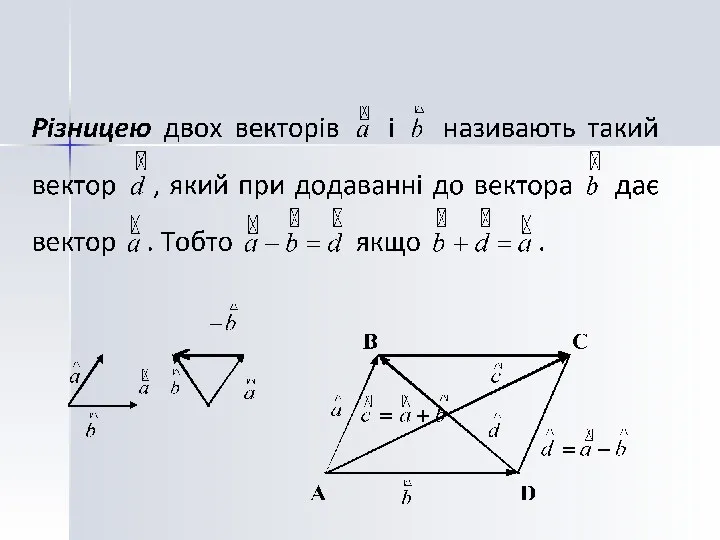
- 4. Лінійні операції над векторами Добуток вектора на число Сума двох векторів Різниця двох векторів Правило паралелограма
- 7. Властивості: - комутативність; - асоціативність; - дистрибутивність по відношенню до множення на число
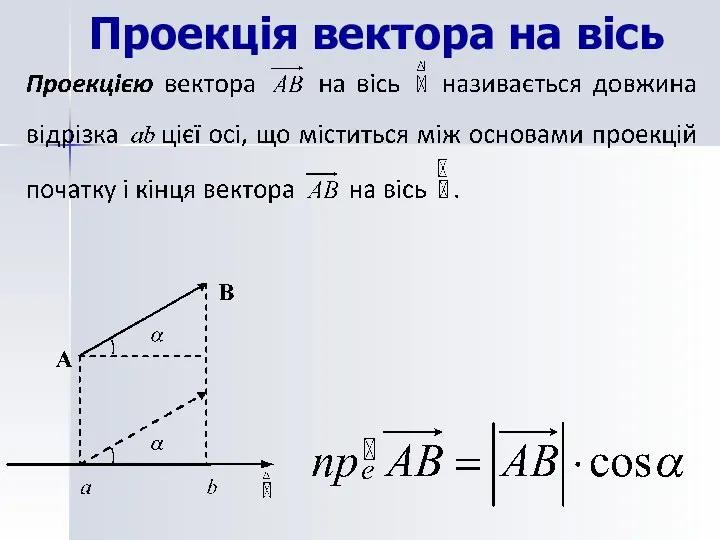
- 9. Проекція вектора на вісь
- 10. Властивості : рівні вектори мають рівні проекції; при множенні вектора на число його проекція на вісь
- 11. Означення
- 12. Теорема Якщо система векторів лінійно залежна, то хоча би один з них можна представити у вигляді
- 13. Означення
- 14. Теорема . Довільні два колінеарні вектори лінійно залежні і, навпаки, два неколінеарних вектори лінійно незалежні. Теорема
- 15. Базисом на прямій називається будь-який ненульовий вектор на цій прямій. Базисом в просторі називаються довільні три
- 16. Теорема
- 17. Теорема
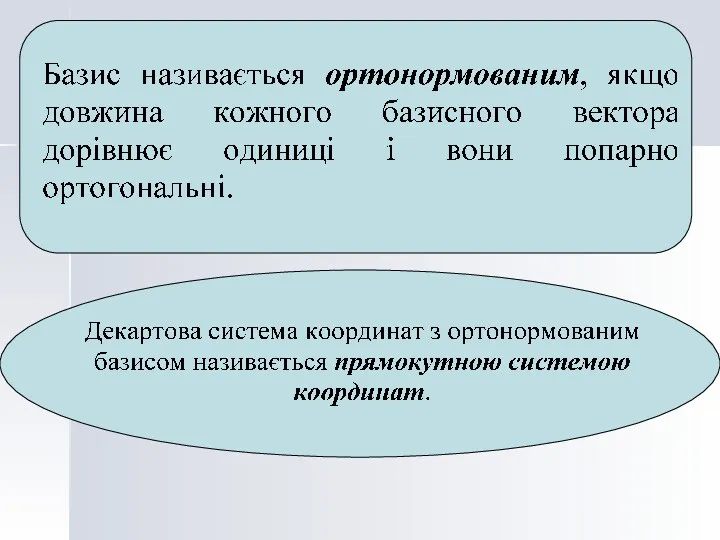
- 18. Означення
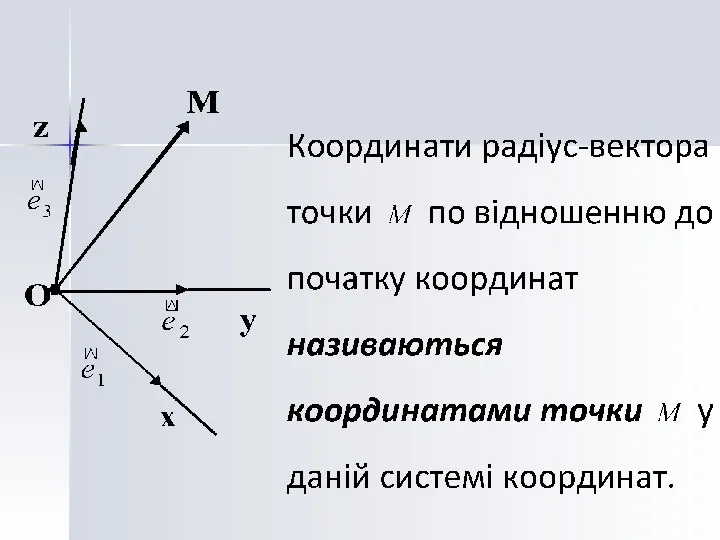
- 19. Декартова системи координат
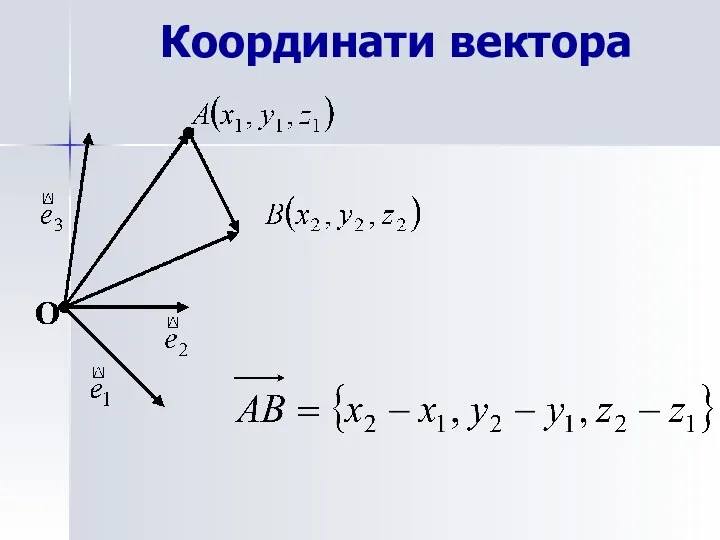
- 21. Координати вектора
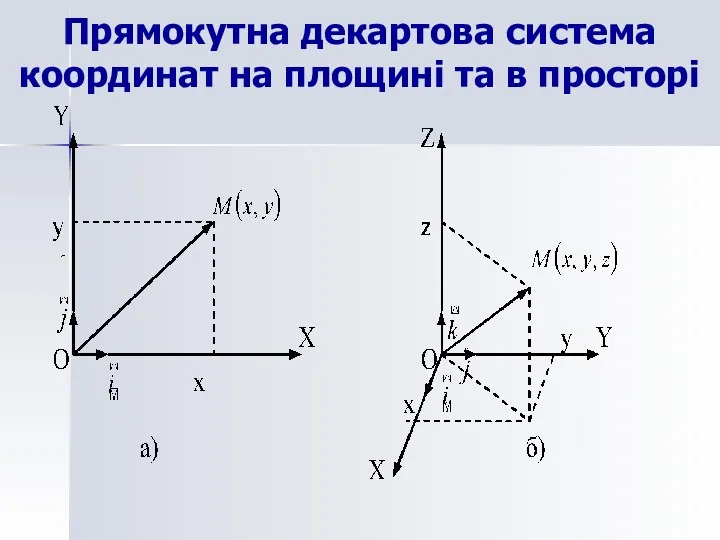
- 24. Прямокутна декартова система координат на площині та в просторі
- 25. Відстань між двома точками На площині В просторі
- 26. Напрямні косинуси
- 27. Ділення відрізка в заданому відношенні Якщо Та
- 28. Означення
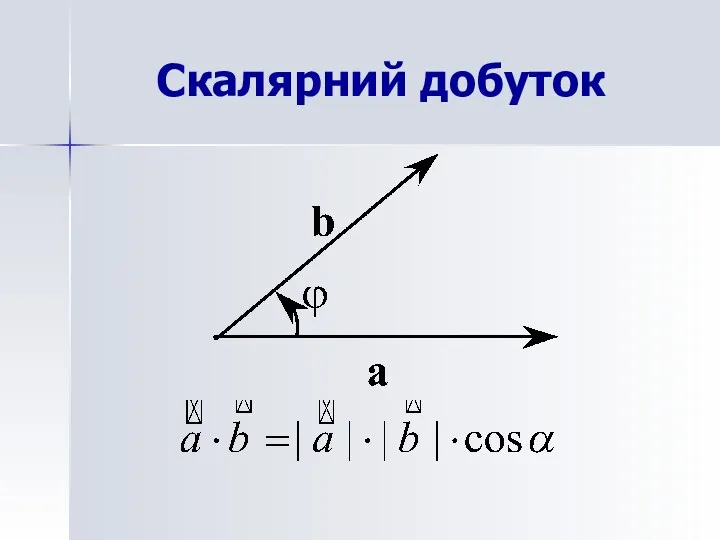
- 29. Скалярний добуток
- 30. властивості:
- 32. Вираз скалярного добутку через координати Якщо , тоді
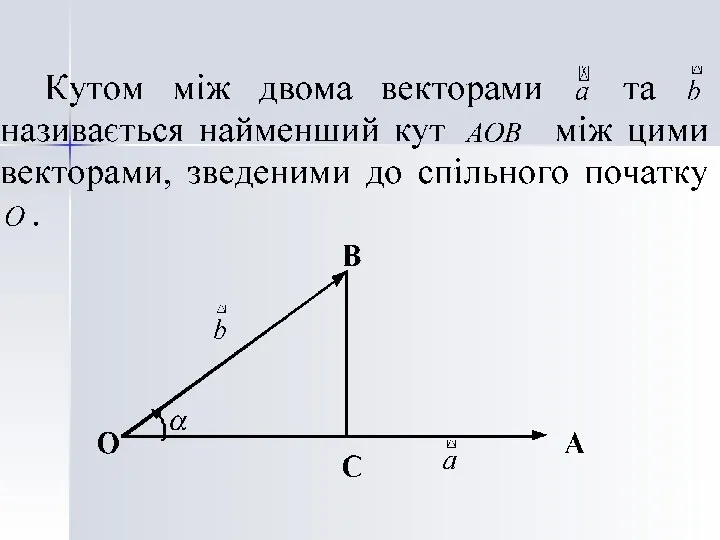
- 33. Застосування: 1. Кут між векторами
- 34. 2. Умова ортогональності двох векторів
- 35. 3. Фізичний зміст якщо матеріальна точка, на яку діє сила, здійснила переміщення , То робота дорівнює
- 37. Векторний добуток
- 38. Властивості: - антикомутативність; асоціативність відносно скалярного множника; дистрибутивність відносно додавання; означає колінеарність векторів і .
- 39. векторний добуток основних ортів
- 40. Вираз векторного добутку через координати Якщо , тоді
- 41. Застосування: 1. умова колінеарності векторів
- 42. 2. Геометричний зміст Площа паралелограма Площа трикутника
- 43. 3. Фізичний зміст Момент сили
- 44. Мішаний добуток трьох векторів
- 45. Геометричний зміст
- 47. Умова компланарності
- 48. Властивості:
- 49. Подвійний векторний добуток
- 51. Скачать презентацию













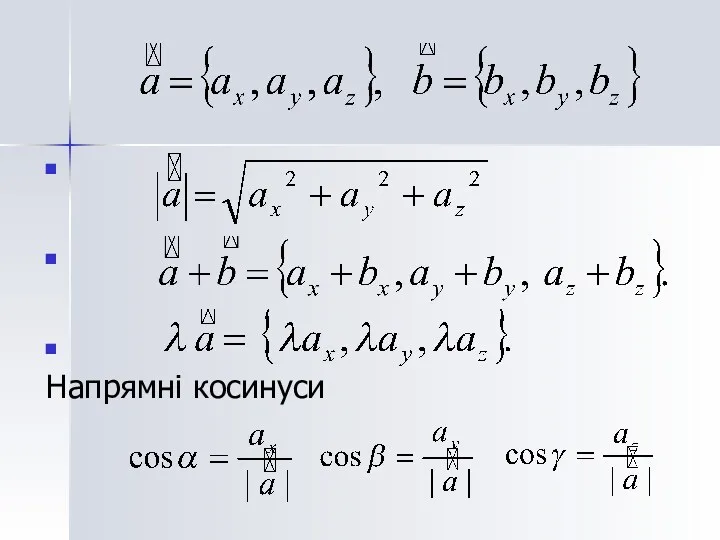






















 Умножение
Умножение Делители и кратные. 5 класс
Делители и кратные. 5 класс Математика вокруг нас. Узоры и орнаменты на посуде
Математика вокруг нас. Узоры и орнаменты на посуде Высказывание. Логические операции
Высказывание. Логические операции Тест по теме: Прямоугольный параллелепипед. Часть 1
Тест по теме: Прямоугольный параллелепипед. Часть 1 Задачи: классификация, методы решения, граничные условия
Задачи: классификация, методы решения, граничные условия Иррациональные уравнения
Иррациональные уравнения Лекция 2 по статистике. Основные категории и понятия статистики
Лекция 2 по статистике. Основные категории и понятия статистики Математические термины в ребусах. Презентация
Математические термины в ребусах. Презентация Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний
Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний Элементы математической статистики, комбинаторики и теории вероятности. Решение задач. Подготовка к ЕГЭ
Элементы математической статистики, комбинаторики и теории вероятности. Решение задач. Подготовка к ЕГЭ Скалярное произведение векторов
Скалярное произведение векторов Закрепление решения задач на движение. Новогоднее путешествие.
Закрепление решения задач на движение. Новогоднее путешествие. Делители и кратные
Делители и кратные Понятие о производной функции, её геометрический и физический смысл
Понятие о производной функции, её геометрический и физический смысл Общие сведения о кривых линиях и поверхностях
Общие сведения о кривых линиях и поверхностях Умножение одночленов. Возведение одночлена в натуральную степень
Умножение одночленов. Возведение одночлена в натуральную степень Многокритериальные задачи. Метод идеальной точки
Многокритериальные задачи. Метод идеальной точки Деление десятичной дроби на десятичную дробь. 5 класс
Деление десятичной дроби на десятичную дробь. 5 класс Способы разложения многочленов на множители
Способы разложения многочленов на множители Готовимся к ОГЭ. Алгебра ( 2 часть)
Готовимся к ОГЭ. Алгебра ( 2 часть) Тест. Задания В1, ЕГЭ по математике
Тест. Задания В1, ЕГЭ по математике Математика. 3 класс. Сложение и вычитание. Приемы устных вычислений в пределах 1000.
Математика. 3 класс. Сложение и вычитание. Приемы устных вычислений в пределах 1000. Тест по математике в форме ЕГЭ
Тест по математике в форме ЕГЭ Обработка результатов эксперимента. Матричное исчисление
Обработка результатов эксперимента. Матричное исчисление Моделирование систем. Классификация моделей
Моделирование систем. Классификация моделей Квадрат. Площадь
Квадрат. Площадь Умножение и деление на 8
Умножение и деление на 8