Содержание
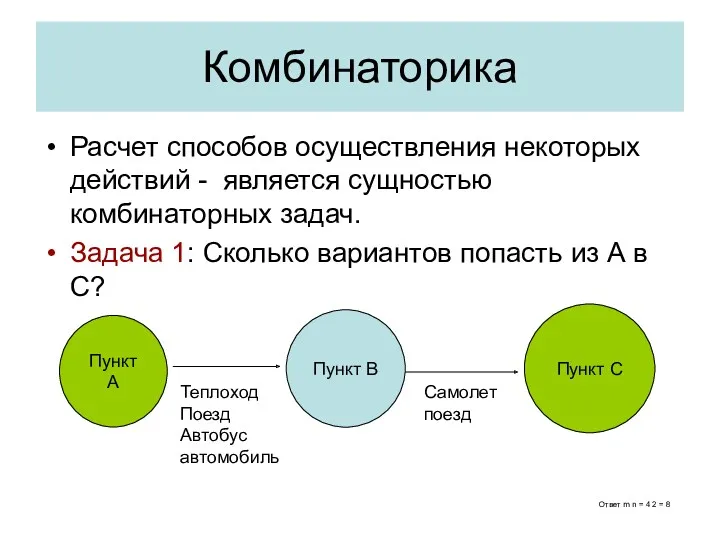
- 2. Комбинаторика Расчет способов осуществления некоторых действий - является сущностью комбинаторных задач. Задача 1: Сколько вариантов попасть
- 3. Введение ЗАДАЧА 2: В соревновании участвуют 16 команд. Сколько способов распределения золотой, серебряной медали и бронзовой
- 4. Основное правило комбинаторики Правило умножения. Если необходимо выполнить по порядку k действий. Первое можно выполнить n1
- 5. Задача Задача 3. Сколько четырех значных чисел можно составить из цифр {1,2,3,4,5}, если А) ни одна
- 6. Задача Задача 4. На гору ведет 7 дорог. Сколько вариантов подняться и спуститься с горы? А
- 7. Вычисление числа элементов суммы множеств Если задано множество А и множество В, то число элементов суммы
- 8. Задача 5 Задача 5. Каждый студент группы либо девушка, либо имеет светлые волосы, либо обожает дискретную
- 9. Решение задачи 5 Пусть А множество студенток – 20. В – множество светловолосых (М и Д)
- 10. Ответ задачи 5 Подставляем числа в формулу вычисления суммы числа трех множеств:
- 11. Теорема о числе элементов объединения множеств Если А1,…,Аn – некоторые множества, то число элементов объединений этих
- 12. Продолжение теоремы Правая часть этого равенства является суммой n слагаемых, где к - тое по порядку
- 13. Упорядоченное множество Определение: множество из которого задан порядок его элементов называется упорядоченным. Каждому элементу множества указан
- 14. Число возможных слов длины k из алфавита мощностью n Пусть задано два множества А – алфавит,
- 15. Принцип математической индукции Пусть имеется конечное упорядоченное множество n натуральных чисел А = {1,2,3,…,n}. Предположим, что
- 16. Принцип математической индукции 1) Если некоторое утверждение справедливо для k=1. 2) из справедливости утверждения для произвольного
- 17. Пример доказательства При n = 1 неравенство выполняется. Предположим, что выполняется неравенство Докажем, что справедливо неравенство
- 18. Понятие собственного подмножества Если каждый элемент множества В принадлежит множеству А, то В подмножество множества А.
- 19. Множество всех его подмножеств Если задано множество А, то можно рассматривать новое множество М(А) – множество
- 20. Пример множества всех подмножеств Пусть А={a,b,c}, тогда М(А)={{a},{b},{c},{a,b},{a,с},{b,с},{a,b,c}, } {{a,b},{a,с},{b,с}} ВОПРОС – сколько разных k –
- 21. Число сочетаний из n по k ТЕОРЕМА: Число всех k - элементарных подмножеств множества А из
- 22. Примеры задач Задача 6. Сколько способов выбора трех книг из пяти. Задача 7. В комиссию надо
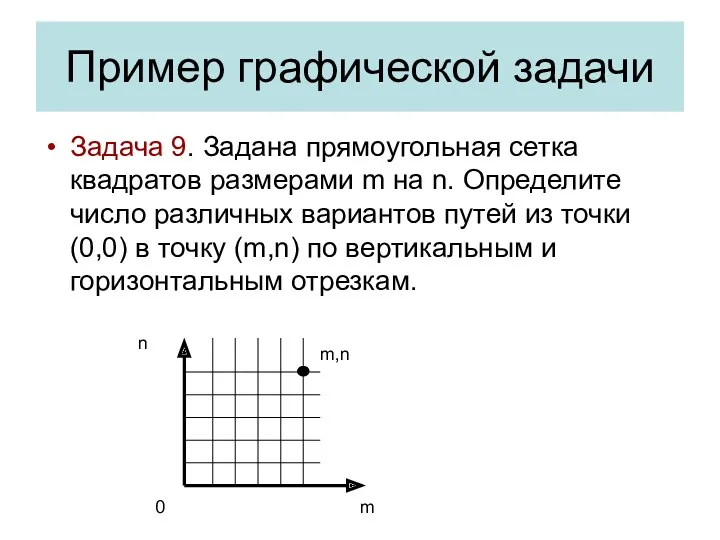
- 23. Пример графической задачи Задача 9. Задана прямоугольная сетка квадратов размерами m на n. Определите число различных
- 24. Теорема о сумме числа сочетаний Число сочетаний из n по k равно сумме числа сочетаний из
- 25. Теорема о сумме числа сочетаний ДОКАЗАТЕЛЬСТВО: Число кратчайших путей из точки (0,0) в точку А(k, n-k)
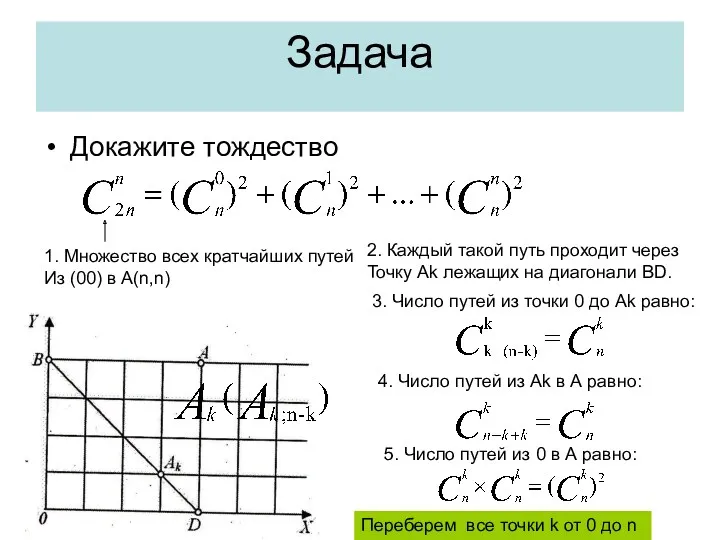
- 26. Задача Докажите тождество 1. Множество всех кратчайших путей Из (00) в А(n,n) 2. Каждый такой путь
- 27. Количество подмножеств данного множества ВОПРОС. Сколько всего подмножеств имеет множество А, состоящее из n элементов, с
- 28. Следствие теоремы Имеет место равенство: Действительно, если число k – элементных подмножеств множества n Элементов, то
- 29. Упорядоченные множества. Перестановки и размещения Множество называется упорядоченным. Если каждому элементу множества противопоставлено некоторое число от
- 30. Варианты перестановок множества Пусть задано множество А из n – элементов, а Pn – число перестановок.
- 31. Примеры Задача 11. Сколькими способами можно поставить 4 книги на полке. Задача 12. Сколькими способами можно
- 32. Число размещений длины k из алфавита n Число размещений длины k из алфавита n определяется формулой:
- 34. Скачать презентацию




























 Модели, описываемые системами двух автономных дифференциальных уравнений
Модели, описываемые системами двух автономных дифференциальных уравнений Координаты вектора
Координаты вектора Интегрирование по частям
Интегрирование по частям Точка рівновіддалена від сторін многокутника
Точка рівновіддалена від сторін многокутника Движение:Скорость,время,расстояние.
Движение:Скорость,время,расстояние. Степень с натуральным показателем. Одночлен
Степень с натуральным показателем. Одночлен Шар. Сфера
Шар. Сфера Решение треугольников
Решение треугольников Задачи на расстояние
Задачи на расстояние История числа Пи
История числа Пи Теорема о равенстве накрест лежащих углов
Теорема о равенстве накрест лежащих углов Вращающие фигуры в архитектуре
Вращающие фигуры в архитектуре Презентация по математике Секунда. УМК Перспектива, 4 класс
Презентация по математике Секунда. УМК Перспектива, 4 класс Қарапайым математикалық түсініктерін қалыптастыру бойынша дидактикалық ойындар картотекасы
Қарапайым математикалық түсініктерін қалыптастыру бойынша дидактикалық ойындар картотекасы Математика. 1 класс. Урок 49. Число ноль. Цифра 0 - Презентация
Математика. 1 класс. Урок 49. Число ноль. Цифра 0 - Презентация Определение арифметической и геометрической прогрессий
Определение арифметической и геометрической прогрессий Деревья. Дерево - граф без циклов
Деревья. Дерево - граф без циклов Задачі на визначення, на скільки років старший. Обчислення значень виразів. Урок №62
Задачі на визначення, на скільки років старший. Обчислення значень виразів. Урок №62 Формулы двойного аргумента. (Часть 1)
Формулы двойного аргумента. (Часть 1)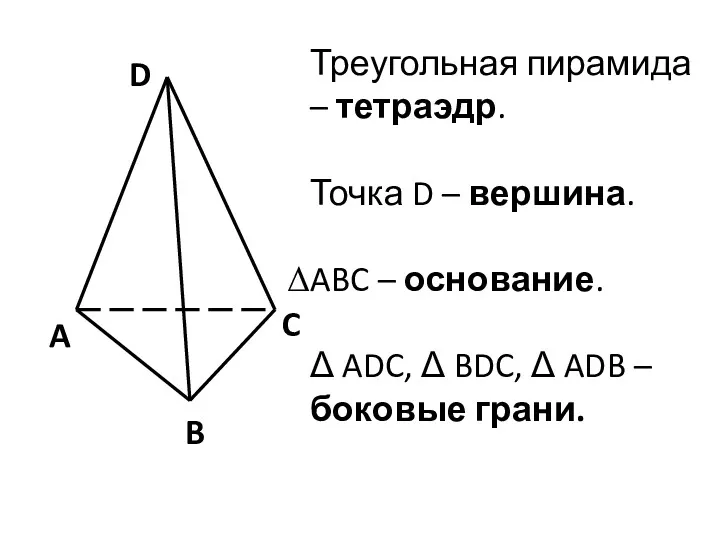 Пирамида и ее свойства
Пирамида и ее свойства Презентация Архитектурные здания
Презентация Архитектурные здания Формулы сокращенного умножения. Квадрат суммы и квадрат разности. ( урок с использованием технологии УДЕ). 7 класс
Формулы сокращенного умножения. Квадрат суммы и квадрат разности. ( урок с использованием технологии УДЕ). 7 класс Статистические таблицы
Статистические таблицы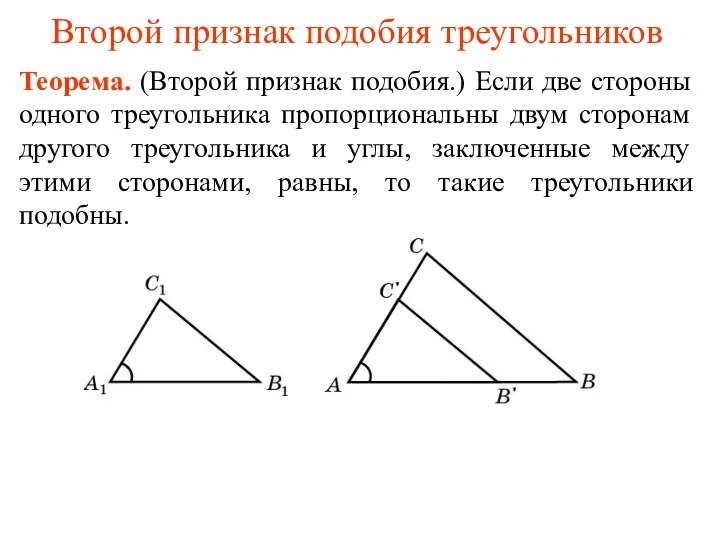 Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Прямоугольный параллелепипед
Прямоугольный параллелепипед Решение неравенств. 9 класс
Решение неравенств. 9 класс Построение треугольника по трём элементам
Построение треугольника по трём элементам Итоговое повторение геометрия. 10 класс
Итоговое повторение геометрия. 10 класс