Содержание
- 2. 1. НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
- 3. Вершины, инцидентные одному и тому же ребру, называются смежными. Так же смежными называются ребра, инцидентные одной
- 5. 2. СПОСОБЫ ЗАДАНИЯ ГРАФОВ
- 6. 1. Аналитический. Если вершине не инцидентно никакое ребро, то эта вершина называется изолированной. Выписываются все ребра
- 7. 2. Геометрический. Каждая вершина графа задается точкой. А ребра, инцидентные паре вершин – кривой. Желательно рисовать
- 8. 3. С помощью матрицы смежности. Задается одинаково для всех графов: Пример. На рисунке изображен граф: Его
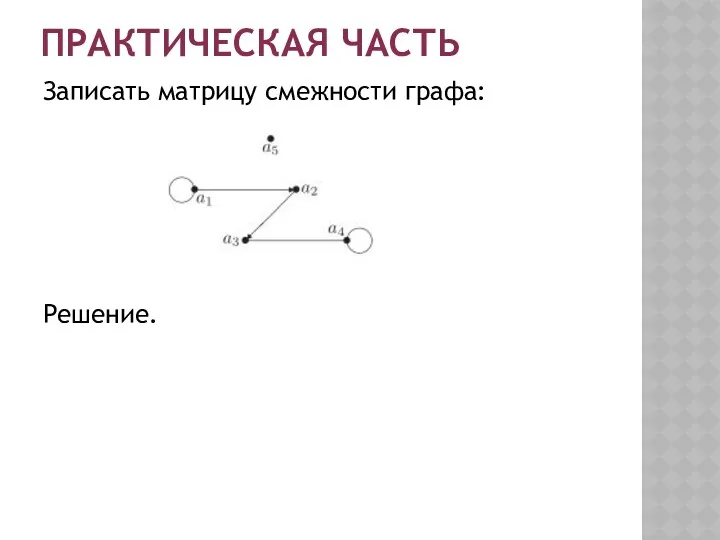
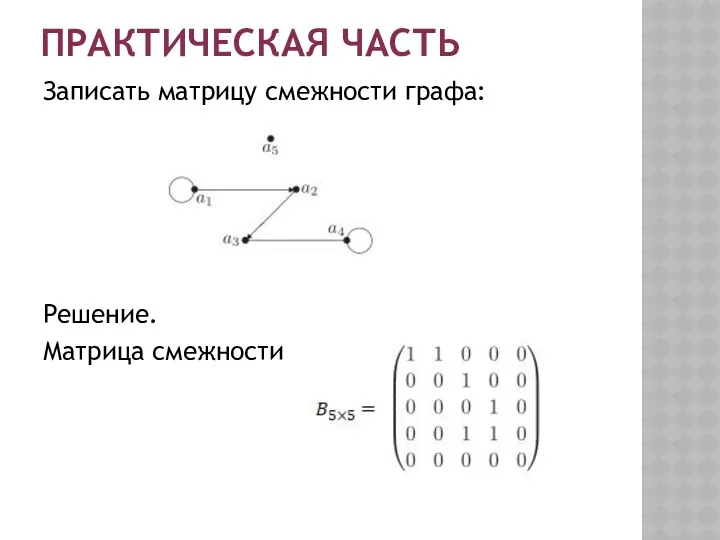
- 9. ПРАКТИЧЕСКАЯ ЧАСТЬ Записать матрицу смежности графа: Решение.
- 10. ПРАКТИЧЕСКАЯ ЧАСТЬ Записать матрицу смежности графа: Решение. Матрица смежности
- 11. 4. С помощью матрицы инцидентности. Для неориентированных графов: Для орграфов: Для петель нужны дополнительные предположения.
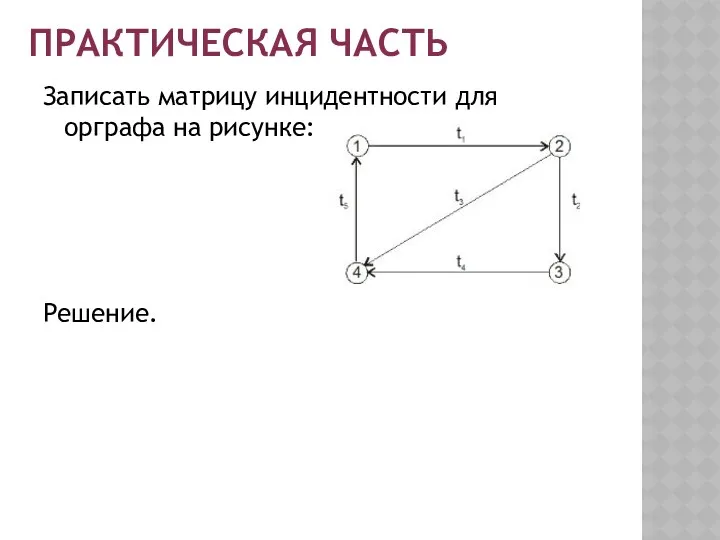
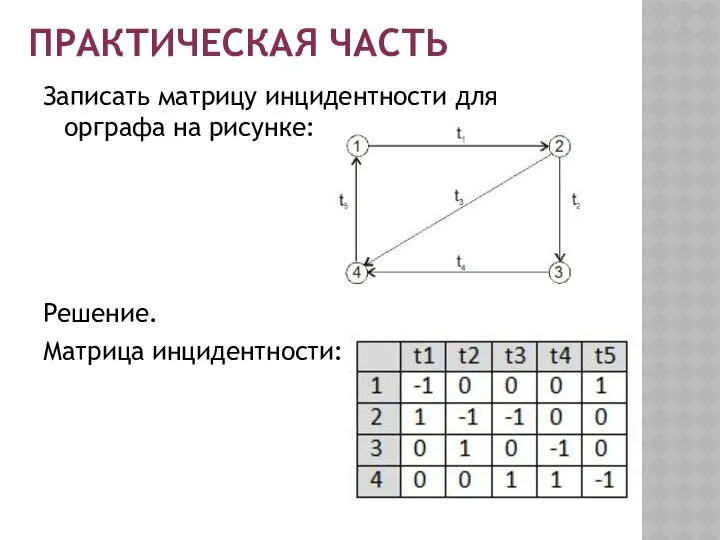
- 12. ПРАКТИЧЕСКАЯ ЧАСТЬ Записать матрицу инцидентности для орграфа на рисунке: Решение.
- 13. ПРАКТИЧЕСКАЯ ЧАСТЬ Записать матрицу инцидентности для орграфа на рисунке: Решение. Матрица инцидентности:
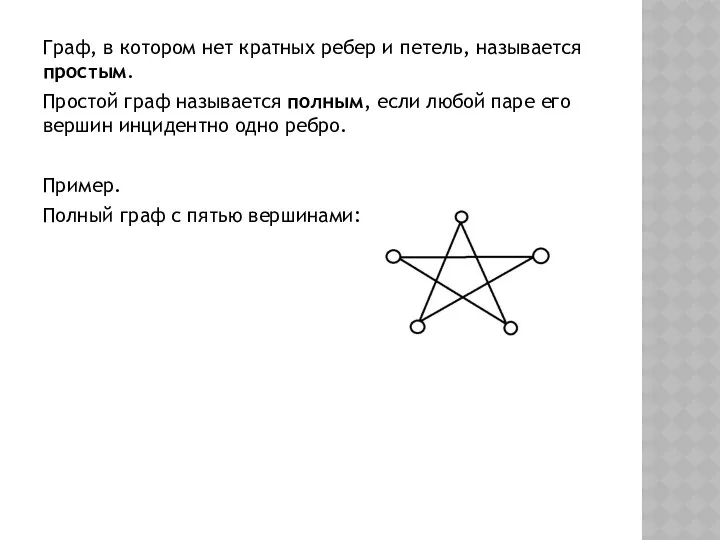
- 14. Граф, в котором нет кратных ребер и петель, называется простым. Простой граф называется полным, если любой
- 15. 3. ЭЙЛЕРОВЫ ГРАФЫ
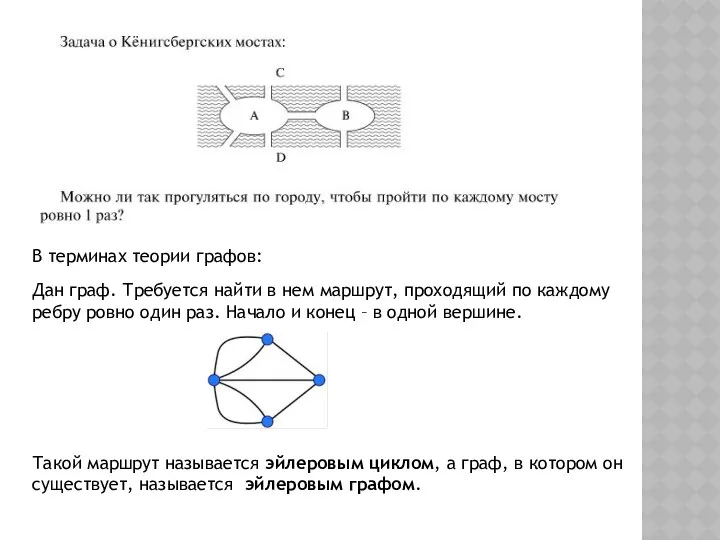
- 16. В терминах теории графов: Дан граф. Требуется найти в нем маршрут, проходящий по каждому ребру ровно
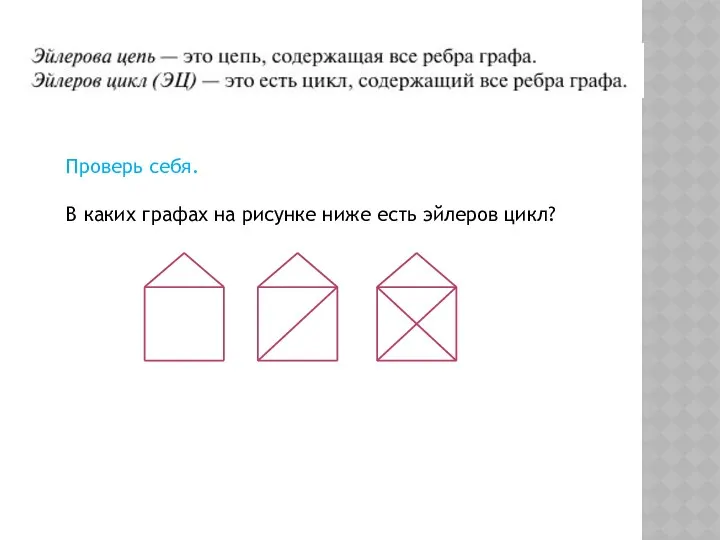
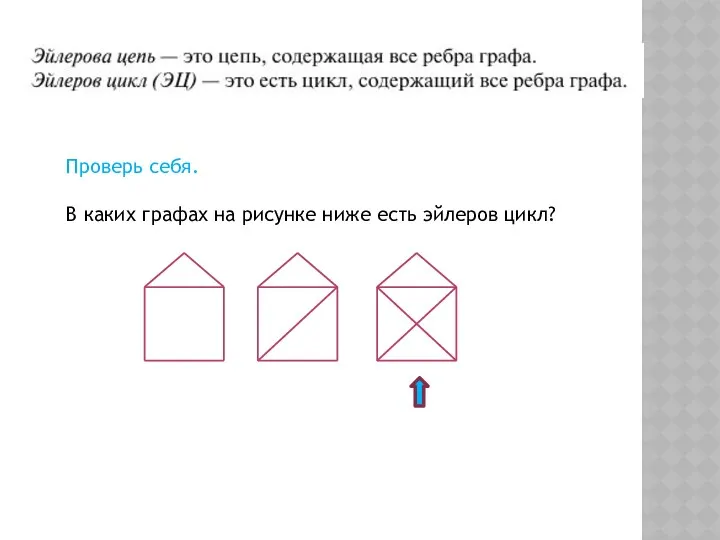
- 17. Проверь себя. В каких графах на рисунке ниже есть эйлеров цикл?
- 18. Проверь себя. В каких графах на рисунке ниже есть эйлеров цикл?
- 19. Степень вершины в графе – это число ребер, инцидентных этой вершине. Критерий эйлеровости графа. Для того,
- 20. 3. МАРШРУТЫ, ЦИКЛЫ, СВЯЗНОСТИ.
- 22. 4. ЗАДАЧА НАХОЖДЕНИЯ МИНИМАЛЬНОГО ОСТОВА.
- 24. 5. I-Я ЗАДАЧА НАХОЖДЕНИЯ МИНИМАЛЬНОГО ПУТИ В ГРАФЕ.
- 26. 6. II-Я ЗАДАЧА НАХОЖДЕНИЯ МИНИМАЛЬНОГО ПУТИ В ГРАФЕ.
- 29. 7. ДВУДОЛЬНЫЕ ГРАФЫ.
- 30. ПАРОСОЧЕТАНИЯ
- 31. МАКСИМАЛЬНЫЕ ПАРОСОЧЕТАНИЯ
- 32. МАКСИМАЛЬНЫЕ ПАРОСОЧЕТАНИЯ
- 33. МАТРИЦА СМЕЖНОСТИ ДВУДОЛЬНОГО ГРАФА [V] = M [W] = N Чтобы найти полное паросочетание, нужно найти
- 35. ЗАДАЧА ОБ ОПТИМАЛЬНОМ НАЗНАЧЕНИИ
- 36. ПОСТАНОВКА ЗАДАЧИ Есть m работников и m работ. Каждый из работников выполняет каждую работу с определенной
- 37. ПОСТАНОВКА ЗАДАЧИ (ПРОДОЛЖЕНИЕ) Требуется распределить работы таким образом, чтобы: - каждый работник выполнял только одну работу,
- 38. ПОСТАНОВКА ЗАДАЧИ (ПРОДОЛЖЕНИЕ) В терминах матрицы эффективности задача состоит в нахождении m элементов, расположенных в разных
- 39. В ТЕРМИНАХ ТЕОРИИ ГРАФОВ: Дан двудольный полный граф с Даны длины ребер. Задача состоит в нахождении
- 40. Паросочетание называется совершенным (из множества v в множество w), если число ребер в нем совпадает с
- 41. Паросочетание называется совершенным (из множества v в множество w), если число ребер в нем совпадает с
- 42. АЛГОРИТМ. ШАГ 1 1. Всем вершинам vi даем метку xi = max среди всех элементов i-й
- 43. АЛГОРИТМ. ШАГ 2 2. Ищем ребра, для которых выполняется условие xi + yj = aij Строим
- 44. АЛГОРИТМ. ШАГ 3 3. В построенном графе ищем максимальное паросочетание. Если найденное паросочетание совершенно, то алгоритм
- 45. НЕМНОГО ТЕОРИИ. ТЕОРЕМА ХОЛЛА Для того, чтобы в двудольном графе существовало совершенное паросочетание, необходимо и достаточно,
- 46. НЕМНОГО ТЕОРИИ. ТЕОРЕМА ХОЛЛА (ПРОДОЛЖЕНИЕ) Если на 3-м шаге алгоритма обнаружено, что найденное максимальное паросочетание не
- 47. 4. Из теоремы Холла существует такое подмножество S из V, что |S|> |ϕ(S)|. Ищем это подмножество.
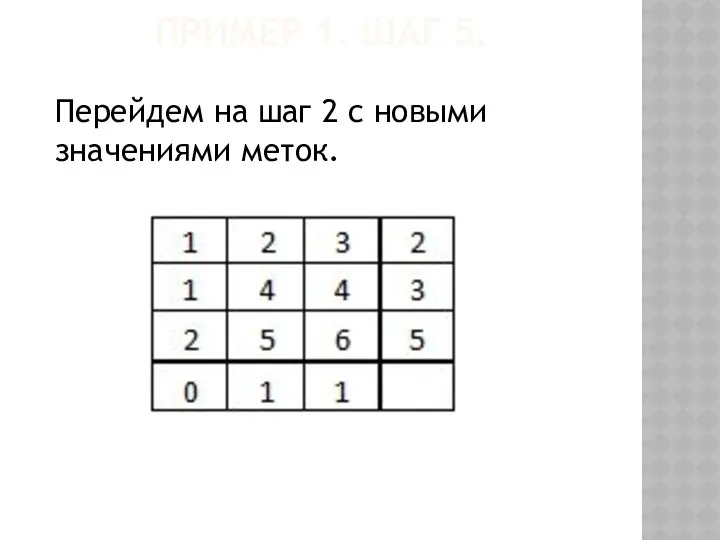
- 48. 5. Переходим на начало шага 2 с новыми значениями меток. АЛГОРИТМ. ШАГ 5
- 49. ВЕСЬ АЛГОРИТМ 1. Всем вершинам vi даем метку xi = max среди всех элементов i-й строки,
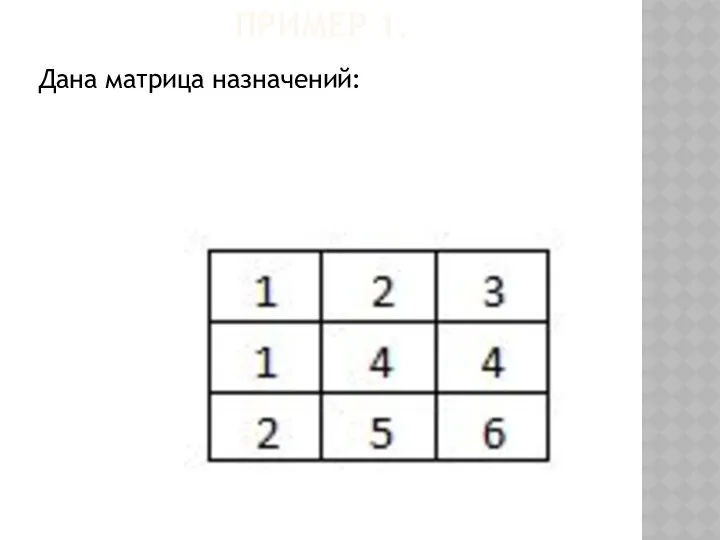
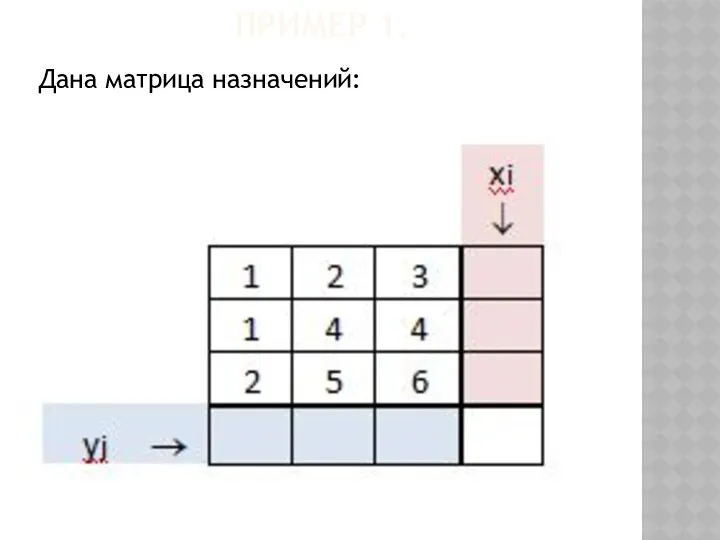
- 50. ПРИМЕР 1. Дана матрица назначений:
- 51. ПРИМЕР 1. Дана матрица назначений:
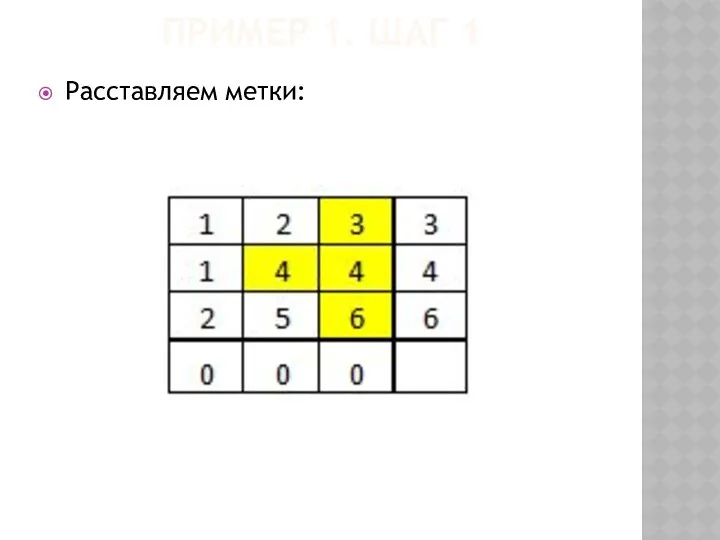
- 52. ПРИМЕР 1. ШАГ 1 Расставляем метки:
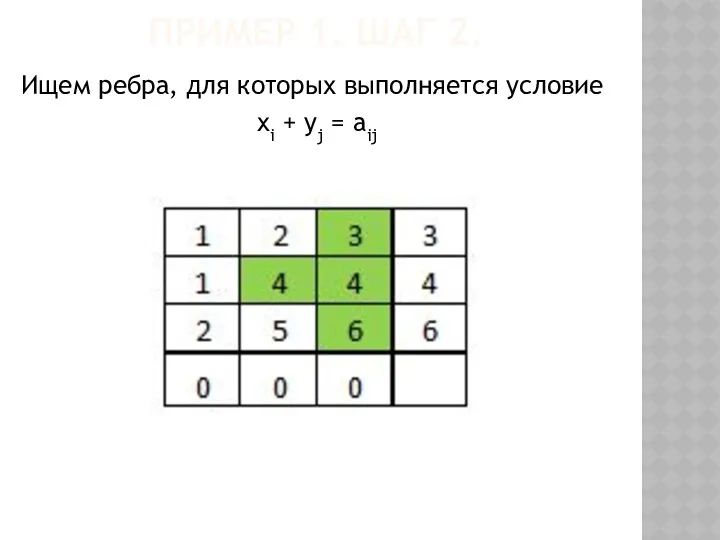
- 53. ПРИМЕР 1. ШАГ 2. Ищем ребра, для которых выполняется условие xi + yj = aij
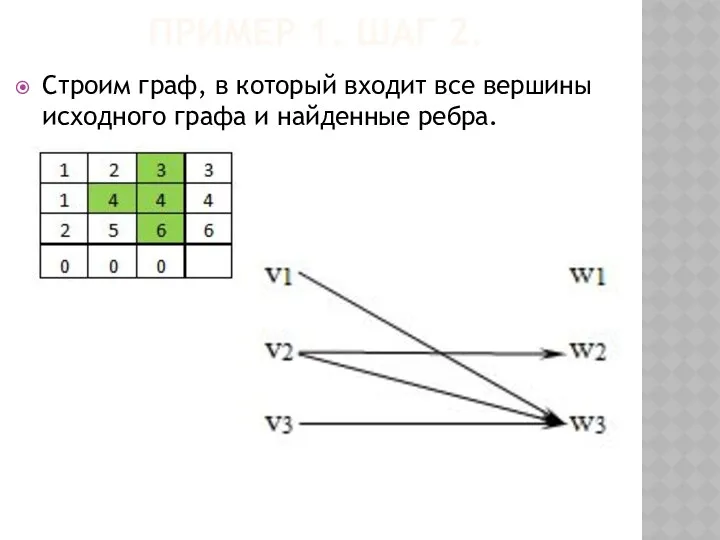
- 54. ПРИМЕР 1. ШАГ 2. Строим граф, в который входит все вершины исходного графа и найденные ребра.
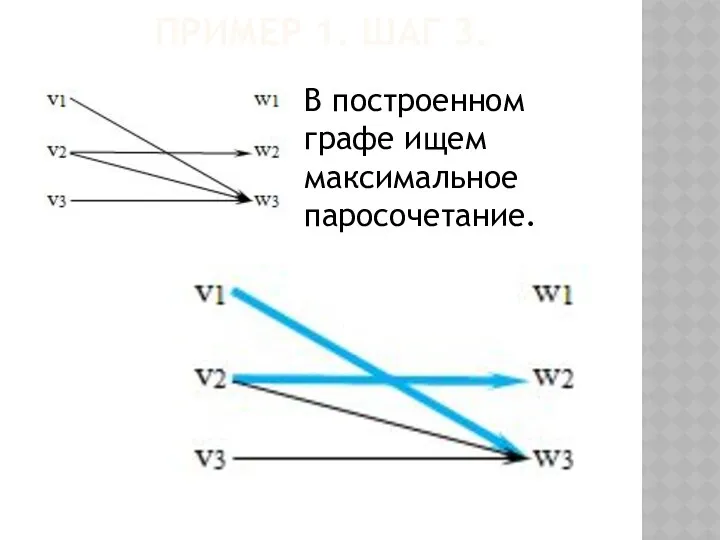
- 55. ПРИМЕР 1. ШАГ 3. В построенном графе ищем максимальное паросочетание.
- 56. АЛГОРИТМ НАХОЖДЕНИЯ МАКСИМАЛЬНОГО ПАРОСОЧЕТАНИЯ 1. Перебираем все ребра в любом порядке. Все несмежные ребра включаем в
- 57. ПРИМЕР 1. ШАГ 4. Найдем подмножество S из V, такое что|S|> |ϕ(S)|.
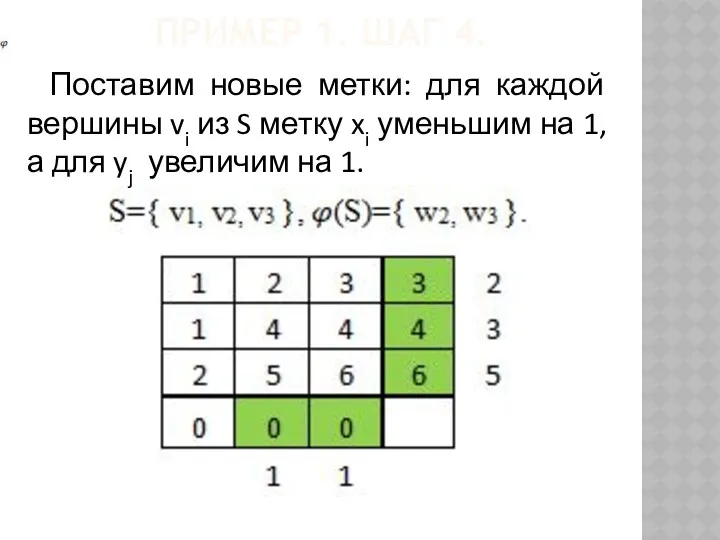
- 58. ПРИМЕР 1. ШАГ 4. Поставим новые метки: для каждой вершины vi из S метку xi уменьшим
- 59. ПРИМЕР 1. ШАГ 5. Перейдем на шаг 2 с новыми значениями меток.
- 60. ПРИМЕР 1. ШАГ 2. Снова ищем ребра, для которых выполняется условие xi + yj = aij
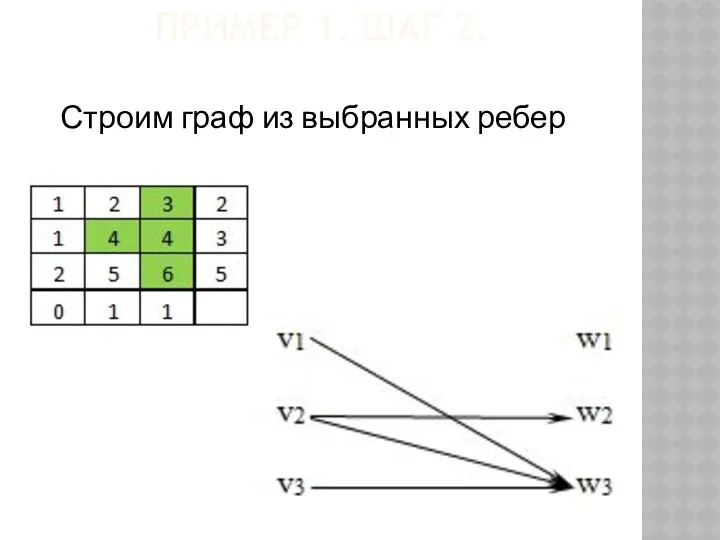
- 61. ПРИМЕР 1. ШАГ 2. Строим граф из выбранных ребер
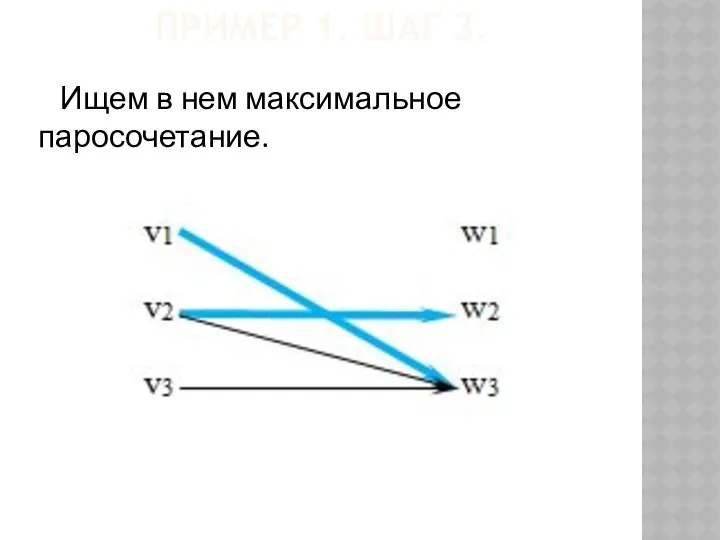
- 62. ПРИМЕР 1. ШАГ 3. Ищем в нем максимальное паросочетание.
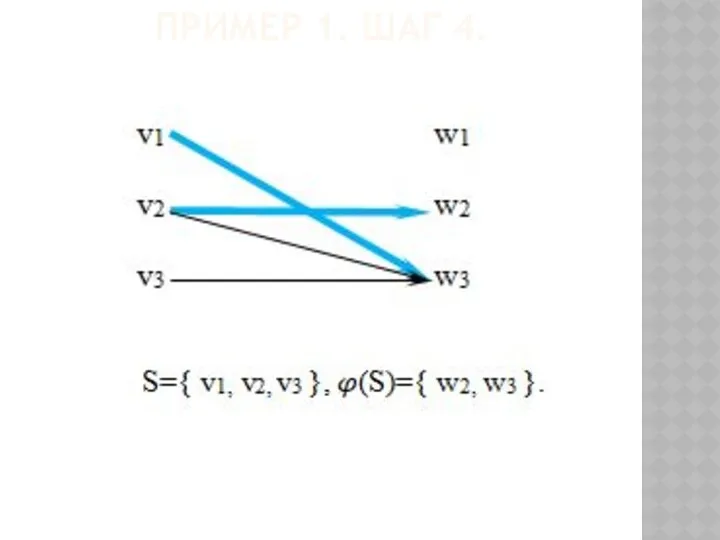
- 63. ПРИМЕР 1. ШАГ 4.
- 64. ПРИМЕР 1. ШАГ 4. Изменяем метки.
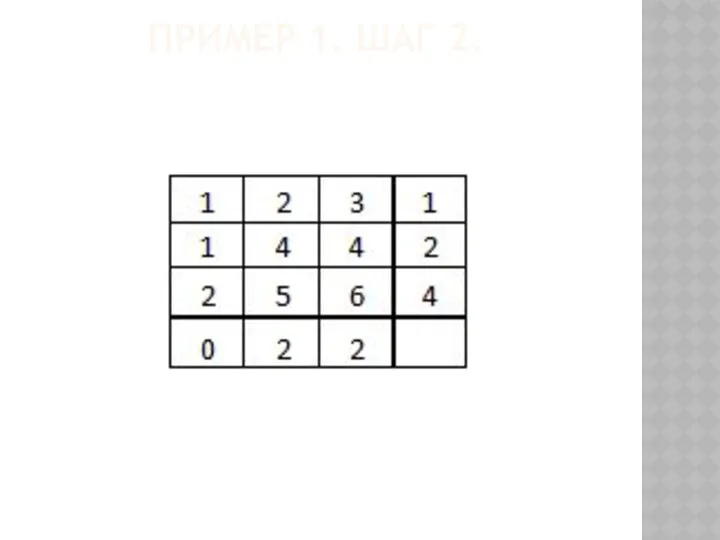
- 65. ПРИМЕР 1. ШАГ 2.
- 66. ПРИМЕР 1. ШАГ 2. Ищем ребра, для которых xi + yj = aij
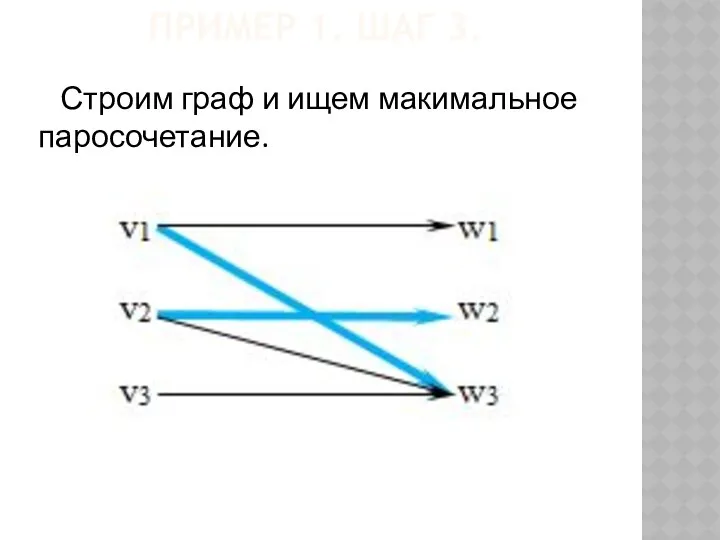
- 67. ПРИМЕР 1. ШАГ 3. Строим граф и ищем макимальное паросочетание.
- 68. ПРИМЕР 1. ШАГ 3.
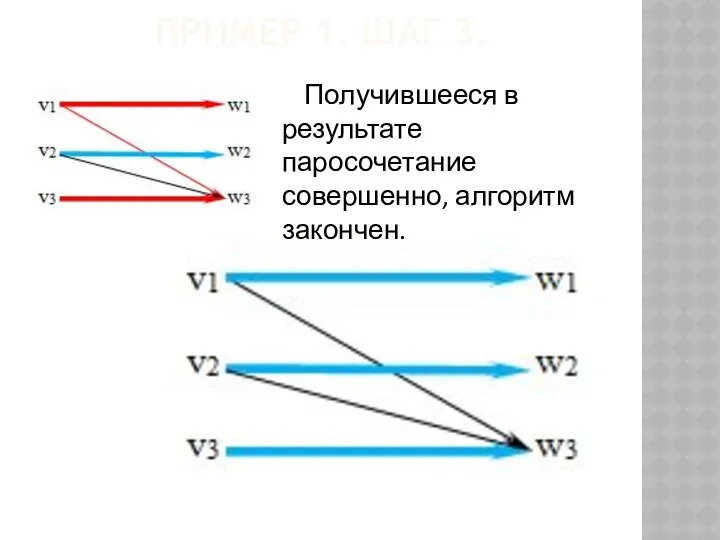
- 69. ПРИМЕР 1. ШАГ 3. Перекрашиваем тонкую цепь.
- 70. ПРИМЕР 1. ШАГ 3. Получившееся в результате паросочетание совершенно, алгоритм закончен.
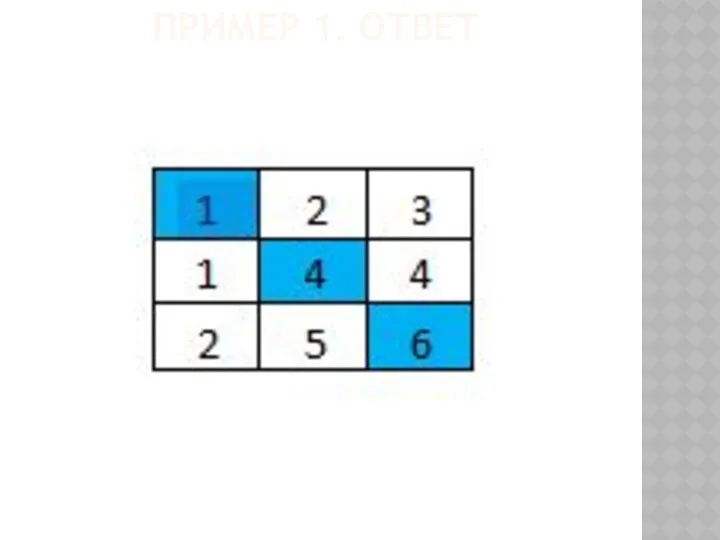
- 71. ПРИМЕР 1. ОТВЕТ
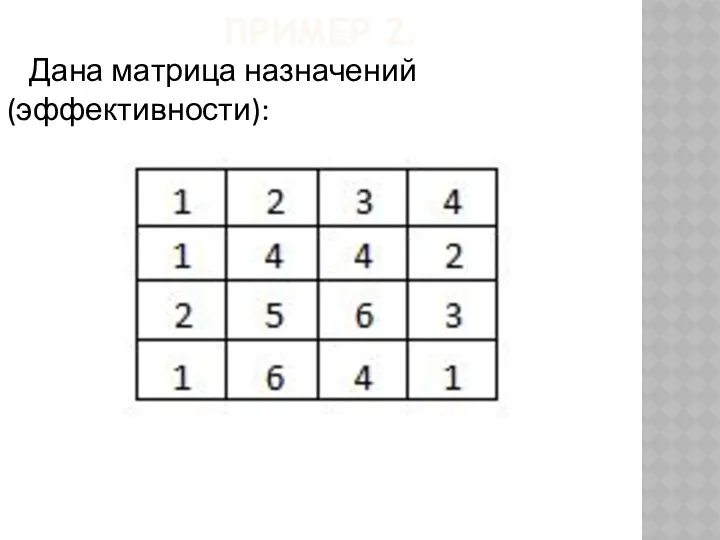
- 72. ПРИМЕР 2. Дана матрица назначений (эффективности):
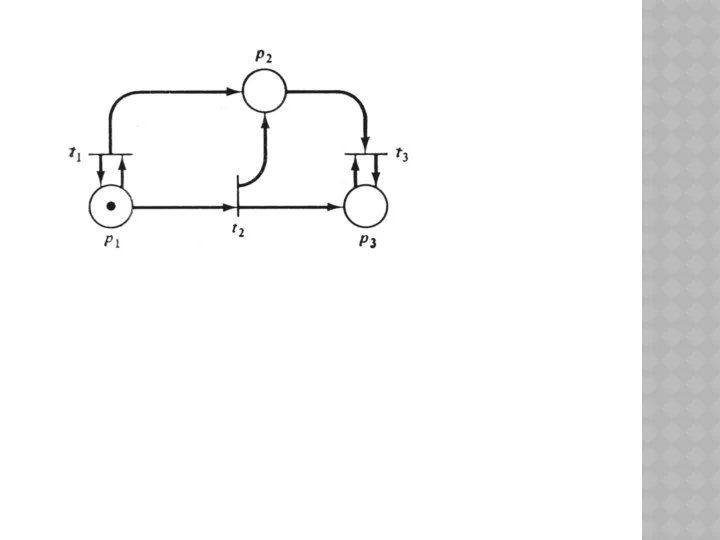
- 73. 8. СЕТИ ПЕТРИ.
- 74. Для моделирования динамических дискретных систем используется математический аппарат, называемый сетями Петри. Сети Петри разрабатывались специально для
- 81. Скачать презентацию






















![МАТРИЦА СМЕЖНОСТИ ДВУДОЛЬНОГО ГРАФА [V] = M [W] = N](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598346/slide-32.jpg)





























 Дидактическая игра на уроке математики в 1 классе
Дидактическая игра на уроке математики в 1 классе Координаты на прямой
Координаты на прямой Изучение вариации
Изучение вариации Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса
Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса Матрицы
Матрицы Перетворення подібності. Гомотетія
Перетворення подібності. Гомотетія Приемы умственной деятельности. Логика для младших школьников
Приемы умственной деятельности. Логика для младших школьников Таблица сложения
Таблица сложения Задание 10: Задачи с прикладным содержанием
Задание 10: Задачи с прикладным содержанием Функция, область определения и область значений функции
Функция, область определения и область значений функции Квадратичная функция, её график и свойства
Квадратичная функция, её график и свойства Презентация-тренажёр Табличное умножение
Презентация-тренажёр Табличное умножение Вселенная математики (Итоговое повторение и обобщение знаний)
Вселенная математики (Итоговое повторение и обобщение знаний) Некоторые свойства прямоугольных треугольников
Некоторые свойства прямоугольных треугольников Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Наибольший общий делитель
Наибольший общий делитель Разрезная геометрия
Разрезная геометрия Подобные слагаемые
Подобные слагаемые Критические, стационарные точки и точки экстремума функции
Критические, стационарные точки и точки экстремума функции Презентация Фольклорные задачи в математике
Презентация Фольклорные задачи в математике Laplace Transform
Laplace Transform Діофантові рівняння (6 клас)
Діофантові рівняння (6 клас) Степенная функция и её график
Степенная функция и её график Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений Обобщающий урок по теме: Деление обыкновенных дробей
Обобщающий урок по теме: Деление обыкновенных дробей Решение задач
Решение задач Урок игра Решение задач
Урок игра Решение задач Призма және оның элементтері
Призма және оның элементтері