Содержание
- 2. Проблема: найти объем мороженицы
- 3. Вычисление объемов тел вращения с помощью определенного интеграла
- 4. Алгебра Определенный интеграл Если функция f(x) непрерывна на промежутке числовой оси, содержащей точки х=а и х=b,
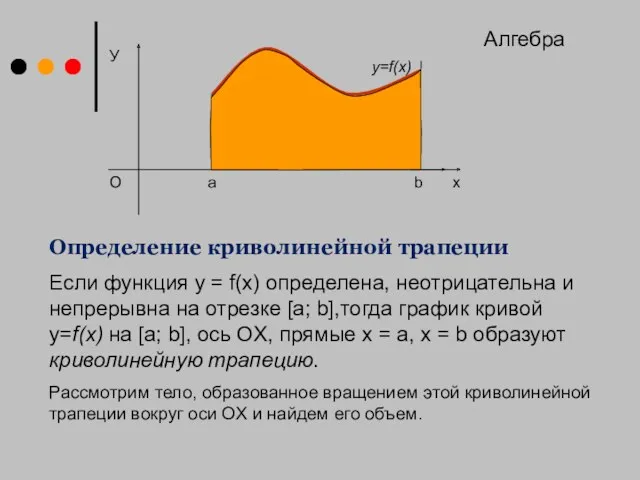
- 5. У х y=f(x) O Определение криволинейной трапеции Если функция y = f(x) определена, неотрицательна и непрерывна
- 6. Определение тела вращения Тело, полученное вращением криволинейной трапеции вокруг её основания, называется телом вращения
- 7. У х y=f(x) O Разобьем отрезок [a;b] на n частей произвольным образом, через каждую точку деления
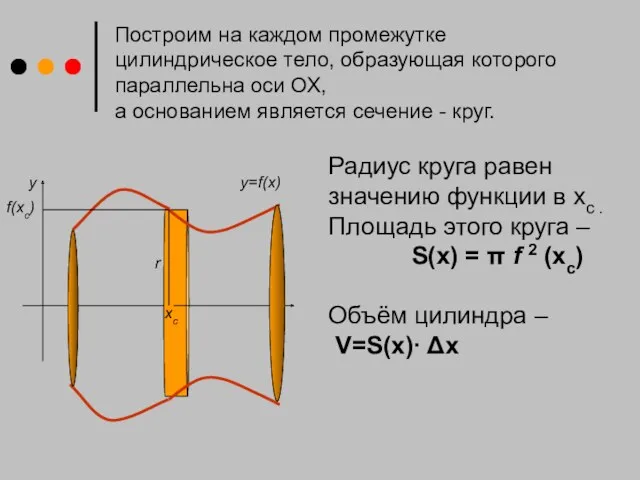
- 8. Построим на каждом промежутке цилиндрическое тело, образующая которого параллельна оси ОХ, а основанием является сечение -
- 9. Объем каждого цилиндра с основанием S(x) и высотой Δx равен S(x)∙ Δx , а объем всего
- 10. Тогда объем тела вращения вокруг оси ОХ: Если тело образовано вращением криволинейной трапеции, образованной функцией у=f(x)
- 11. Замечание! Объем тела вращения вычисляется по одной из формул: ,если вращение криволинейной трапеции вокруг оси ОХ.
- 12. Алгоритм решения задач: Сделать приблизительный график заданных функций, ограничивающих плоскую фигуру, при вращении которой образуется тело
- 13. Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг оси ОХ. Найдите объём тела
- 14. Задача. Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг оси ОХ. Найдите объём тела
- 15. Теперь, давайте, рассмотрим башню для радиостанции в Москве на Шаболовке, построенной по проекту русского инженера, почётного
- 16. Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;4] вокруг оси ОУ. Найдите объём тела
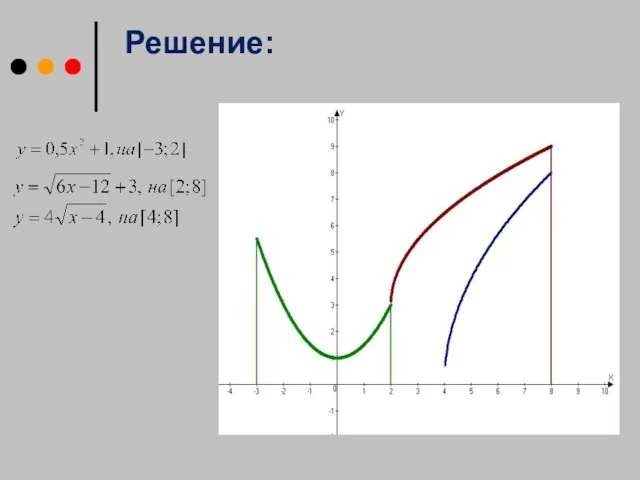
- 17. Решение проблемы: Как найти объем мороженицы? Поверхность тела получена вращением фигуры, образованной графиками функций:
- 18. Решение:
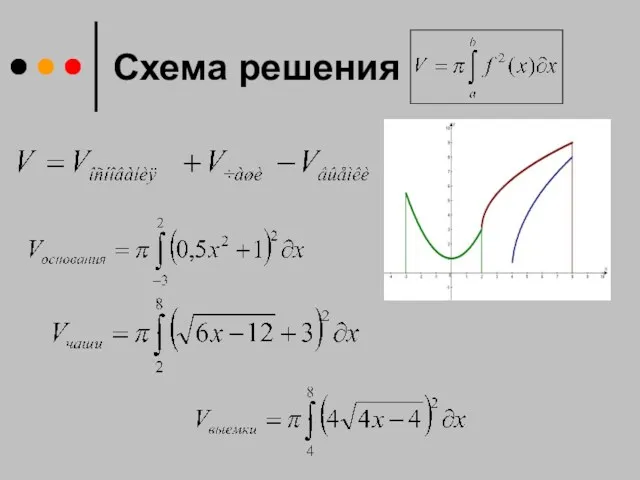
- 19. Схема решения
- 20. Вычисление определённых интегралов
- 22. Скачать презентацию




![У х y=f(x) O Разобьем отрезок [a;b] на n частей](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432963/slide-6.jpg)




![Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432963/slide-12.jpg)
![Задача. Пусть тело образовано вращением функции у=0,5x на отрезке [0;4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432963/slide-13.jpg)

![Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432963/slide-15.jpg)


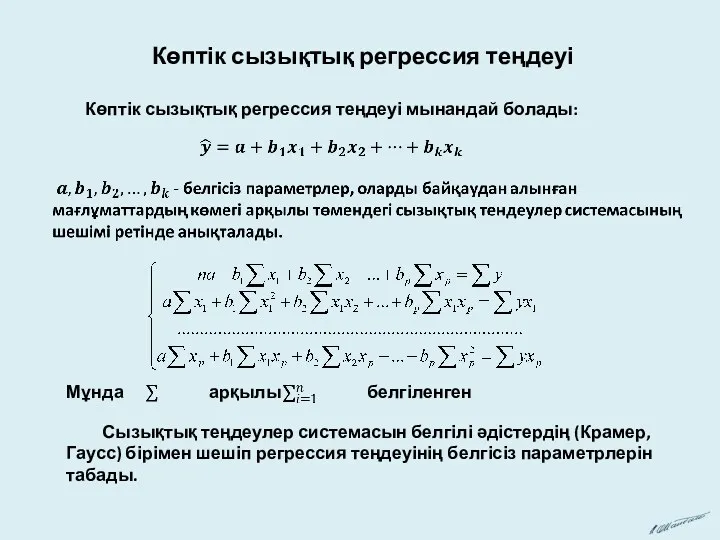 Көптік сызықтық регрессия теңдеуі
Көптік сызықтық регрессия теңдеуі Функции и их свойства
Функции и их свойства Степень с натуральным показателем. Устный опрос
Степень с натуральным показателем. Устный опрос Уравнения. Открытый урок алгебры
Уравнения. Открытый урок алгебры урок математики по теме число и цифра 3
урок математики по теме число и цифра 3 Конкретный смысл действия деления
Конкретный смысл действия деления Углы, связанные с окружностью
Углы, связанные с окружностью Задания на нумерацию чисел в концентре 10
Задания на нумерацию чисел в концентре 10 Математик – бизнесмен. Математическая игра для 5 классов
Математик – бизнесмен. Математическая игра для 5 классов Обобщение и систематизация знаний по теме: многоугольники и многогранники
Обобщение и систематизация знаний по теме: многоугольники и многогранники Деление десятичной дроби на на натуральное число. 5 класс
Деление десятичной дроби на на натуральное число. 5 класс Умножение числа 3 и на 3
Умножение числа 3 и на 3 Осевая и цетральная симметрии
Осевая и цетральная симметрии Последовательное индикаторное моделирование (SIS)
Последовательное индикаторное моделирование (SIS) Умножение и деление обыкновенных дробей. 6 класс
Умножение и деление обыкновенных дробей. 6 класс Цилиндр
Цилиндр Случайные величины
Случайные величины Длина окружности. 6 класс
Длина окружности. 6 класс Презентация УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ по теме Смежные и вертикальные углы углов треугольника
Презентация УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ по теме Смежные и вертикальные углы углов треугольника Среднее арифметическое. 6 класс
Среднее арифметическое. 6 класс Разработка урока с презентацией Решение задач на движение в противоположных направлениях
Разработка урока с презентацией Решение задач на движение в противоположных направлениях Початкові відомості зі стереометрії. Конус
Початкові відомості зі стереометрії. Конус Уравнение данной линии
Уравнение данной линии Урок математики по теме Вычитание, знак минус
Урок математики по теме Вычитание, знак минус Число и цифра 1-10
Число и цифра 1-10 Тригонометрия. Леонард Эйлер
Тригонометрия. Леонард Эйлер Сложение и вычитание десятичных дробей (интегрированный урок в 5 классе: математика и окружающий мир)
Сложение и вычитание десятичных дробей (интегрированный урок в 5 классе: математика и окружающий мир) Презентацияурок математики 1 класс( Космическое путешествие ) .
Презентацияурок математики 1 класс( Космическое путешествие ) .