Содержание
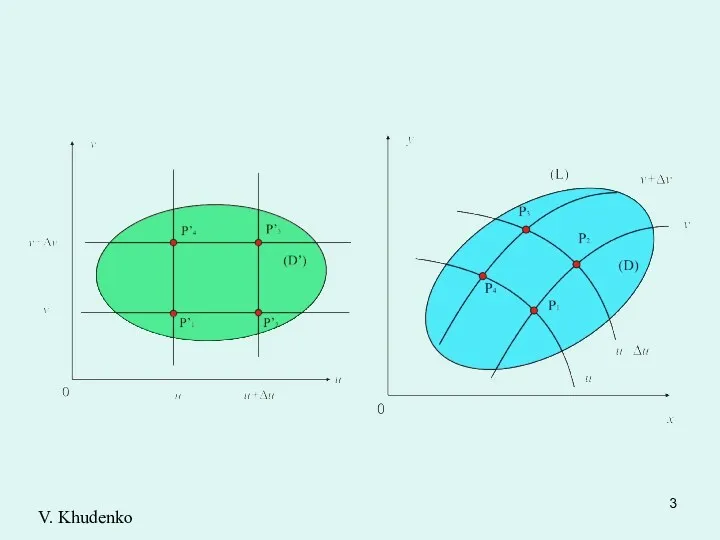
- 2. Замена переменных в двойном интеграле Пусть в плоскости Оху задана область (D), ограниченная линией (L). Предположим,
- 3. V. Khudenko
- 4. Разобьем область прямыми , на прямоугольные площадки. Тогда область (D) соответствующими кривыми линиями разобьется на криволинейные
- 5. Заменим приращения функций дифференциалами V. Khudenko
- 6. Полученные выражения дают основание считать четырехугольник параллелограммом со сторонами V. Khudenko
- 7. Введем обозначение Определитель I называется функциональным определителем функций и или якобианом . Имеет место равенство: Тогда
- 8. Замечание Переход к полярным координатам в двойном интеграле является частным случаем при u=r и v=φ. Тогда
- 9. Вычисление тройного интеграла в цилиндрических координатах Якобиан для случая трех переменных Формула замены переменных для тройного
- 10. В случае перехода к цилиндрическим координатам связь между декартовыми и цилиндрическими координатами: Тогда определитель Якоби V.
- 11. а формула замены переменных при переходе к цилиндрическим координатам примет вид V. Khudenko
- 13. Таким образом интеграл, после расстановки пределов интегрирования запишется в виде V. Khudenko
- 14. Пример Расставить пределы интегрирования в тройном интеграле и вычислить его значение в случае Область ограничена поверхностями:
- 17. Следовательно, область (V) задана неравенствами: Тогда С учетом того, что имеем V. Khudenko
- 18. Вычисление тройного интеграла в сферических координатах Положим u=ρ, v=φ, w=θ. Зависимость между декартовыми и сферическими координатами
- 19. формула замены переменных применительно к сферическим координатам примет вид V. Khudenko
- 21. Получаем формулу V. Khudenko
- 22. Пример Расставить пределы интегрирования в тройном интеграле, если область (V) представляет собой часть пространства. Ограниченную поверхностями
- 24. Уравнение сфер: ,тогда V. Khudenko
- 26. Скачать презентацию





















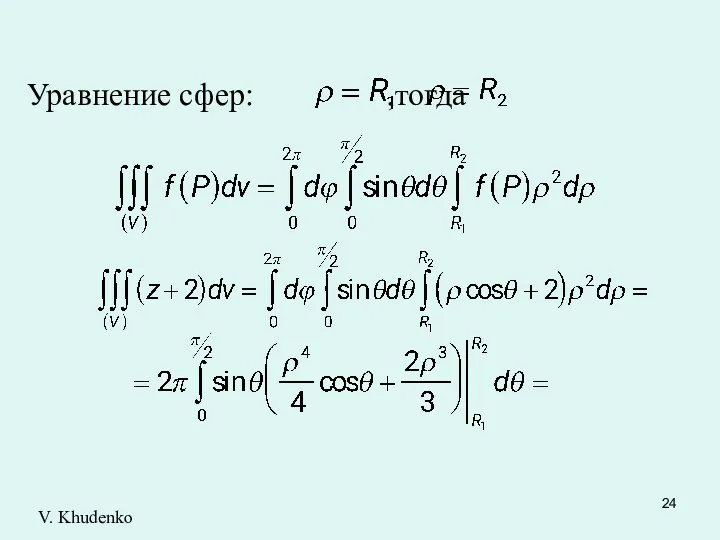
 Презентация Как люди научились считать
Презентация Как люди научились считать Обчислення на основі нумерації. Знаходження невідомого доданка. Складання задачі за числовими даними. Урок №112
Обчислення на основі нумерації. Знаходження невідомого доданка. Складання задачі за числовими даними. Урок №112 Погрешности измерений
Погрешности измерений Целочисленное программирование
Целочисленное программирование Функции: свойства, графики
Функции: свойства, графики Работа по геометрии Как мы видим то, что видим (пояснительная записка + презентация)
Работа по геометрии Как мы видим то, что видим (пояснительная записка + презентация) 10 способов решения квадратных уравнений
10 способов решения квадратных уравнений Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Брейн - ринг. Математическая игра
Брейн - ринг. Математическая игра Значения тригонометрических функций
Значения тригонометрических функций Совместные действия с рациональными числами
Совместные действия с рациональными числами Окружность. Задачи
Окружность. Задачи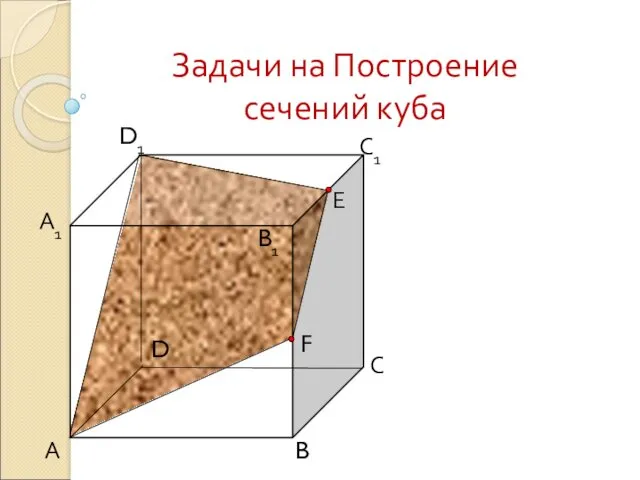 Задачи на Построение сечений куба
Задачи на Построение сечений куба Преобразование рациональных выражений
Преобразование рациональных выражений Математика о вреде курения. Урок-проблема для 7 класса часть 1
Математика о вреде курения. Урок-проблема для 7 класса часть 1 Десятичные дроби
Десятичные дроби Интегрированная система Maple
Интегрированная система Maple Разложение квадратного трехчлена на множители
Разложение квадратного трехчлена на множители Занимательная математика
Занимательная математика Презентация Состав 7 1 класс УМК Гармония
Презентация Состав 7 1 класс УМК Гармония Презентация Математика и конструирование.
Презентация Математика и конструирование. Графический способ решения систем уравнений
Графический способ решения систем уравнений Презентация Учимся правильно писать цифры. 1 класс
Презентация Учимся правильно писать цифры. 1 класс Случаи сложения вида +4
Случаи сложения вида +4 Устный счет на урок математики 2 класс
Устный счет на урок математики 2 класс Разминка для ума
Разминка для ума Презентация к занятиюФея математики
Презентация к занятиюФея математики Теорема Безу. Схема Горнера
Теорема Безу. Схема Горнера